Histograms-And-Frequency-Polygons gcse Edexcel

课 Progress

0% Complete

Exam code:1ST0

Frequency Polygons

What is a frequency polygon?

Frequency polygons are a very simple way of showing frequencies for continuous, grouped data
- They give a quick guide to how frequencies change from one class interval to the next

What are the key features of a frequency polygon?

Apart from plotting and joining up points with straight lines there are 3 rules for frequency polygons:
- Plot points at the midpoint of class intervals
- Unless one of the frequencies is 0 do not join the frequency polygon to the x-axis
- Do not join the first point to the last one
The result is not actually a polygon
- It’s more of an ‘open’ polygon that ‘floats’ in mid-air!
You may be asked to draw a frequency polygon and/or use it to make comments and compare data

How do I draw a frequency polygon?

This is most easily shown by an example
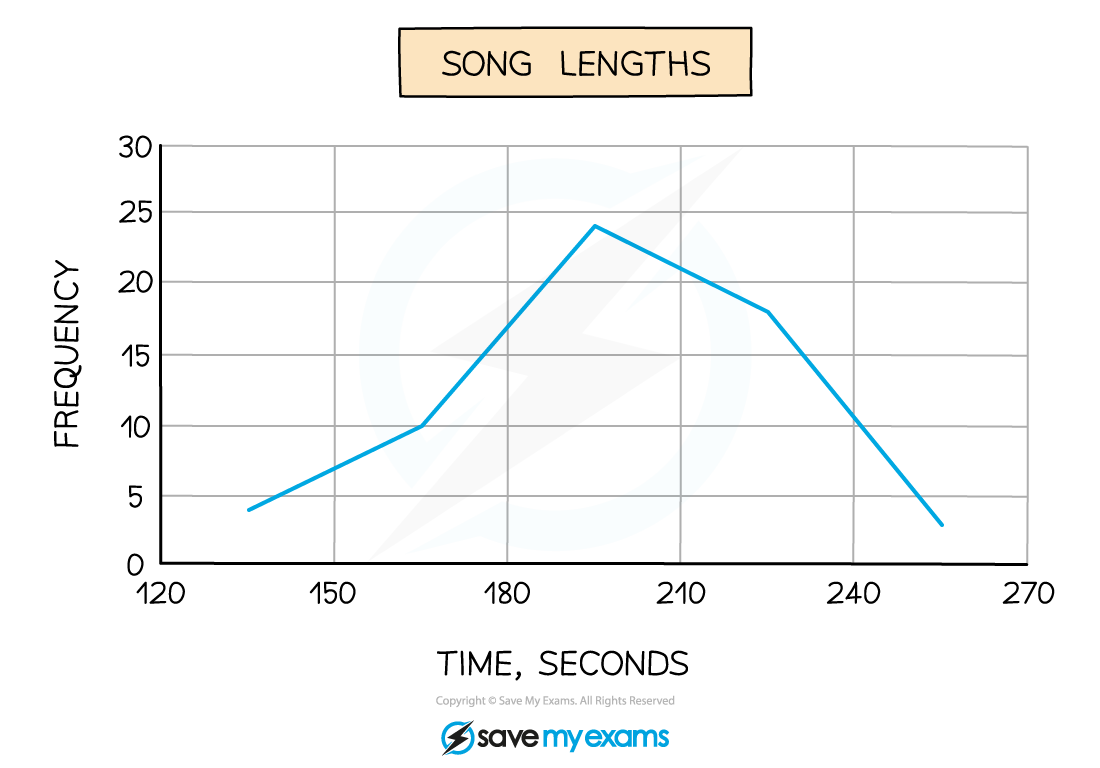
- e.g. The lengths of 59 songs, in seconds, are recorded in the table below

Song length t seconds	Frequency
120 ≤ t < 150	4
150 ≤ t < 180	10
180 ≤ t < 210	24
210 ≤ t < 240	18
240 ≤ t < 270	3

Frequencies are plotted at the midpoints of the class intervals, so in this case we would plot the points (135, 4), (165, 10), (195, 24), (225, 18) and (255, 3).
Join these up with straight lines (but do not join the last to the first!)

Song Length FP, IGCSE & GCSE Maths revision notes

If you have a histogram with equal class widths
- then a frequency polygon can be drawn
  - by marking the points at the centres of the tops of all the histogram bars
  - and joining those points together to make the ‘polygon’

How do I use and interpret a frequency polygon?

Think about what you could you say about the data above, particularly by looking at the diagram only
- The two things to look for are averages and spread
  - The modal class is 180 ≤ t < 210
    - Because the graph reaches its highest point there
    - It would be acceptable to say that 195 seconds is (an estimate of) the modal song length
  - The diagram (rather than the table) shows (an estimate of) the range of song lengths is 255 – 135 = 120 seconds
    - i.e. midpoint of highest class interval minus midpoint of lowest class interval
- If 2 frequency polygons are drawn on the same graph comparisons between the 2 sets of data can be made

Examiner Tips and Tricks

Jot down the midpoints next to the frequencies so you are not trying to work them out in your head while also concentrating on actually plotting the points

Worked Example

A local council ran a campaign to encourage households to waste less food.

To compare the impact of the campaign the council recorded the weight of food waste produced by 30 households in a week both before and after the campaign.

The results are shown in the table below.

Food waste w kg	Frequency (before campaign)	Frequency (after campaign)
1 ≤ w < 1.4	3	5
1.4 ≤ w < 1.8	4	8
1.8 ≤ w < 2.2	8	14
2.2 ≤ w < 2.6	10	3
2.6 ≤ w < 3	5	1

(a) On the same diagram, draw two frequency polygons, one for before the council’s campaign and one for after.

Remember to include a key to show which frequency polygon is which.

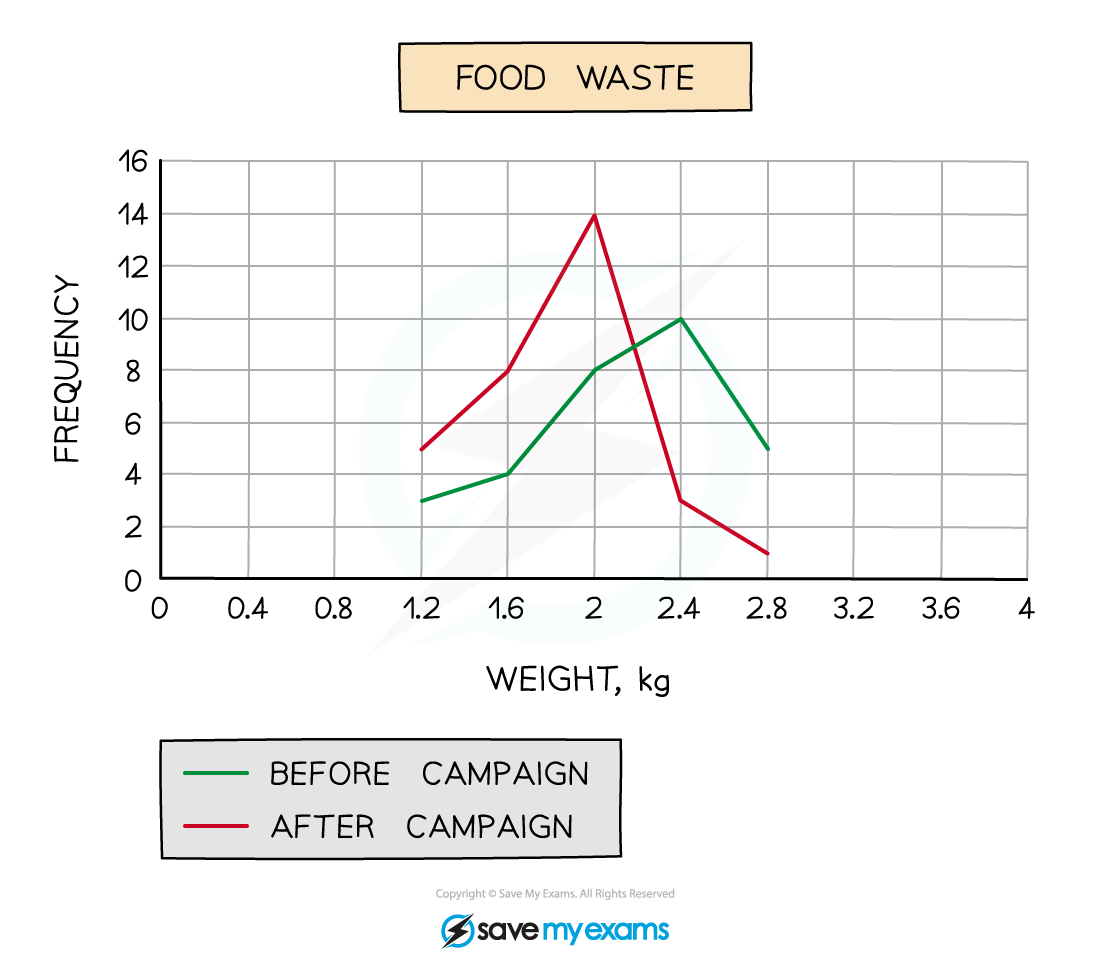
Food-Waste-FP, downloadable IGCSE & GCSE Maths revision notes

(b) Comment on whether you think the council’s campaign has been successful or not and give a reason why.

Remember to look for average(s) and/or spread
The mode (average) is appropriate in this case.

The council campaign has been successful as the modal amount of waste has decreased from 2.4 kg of food waste per week to 2 kg

Frequency Density

What is frequency density?

Frequency density is given by the formula
- $frequency space density equals fraction numerator frequency over denominator class space width end fraction$
  - This formula is not on the exam formula sheet, so you need to remember it
Frequency density is used with grouped data (i.e. data grouped by class intervals)
- It is useful when the class intervals are of unequal width
- It provides a measure of how dense data is within its class interval
  - relative to the width of the interval
- For example,
  - 10 data values spread over a class interval of width 20 would have a frequency density of $10 over 20 equals 1 half$
  - 20 data values spread over a class interval of width 100 would have a frequency density of <img alt=”20 over 100 equals 1 fifth” data-mathml='<math ><semantics><mrow><mfrac><mn>20</mn><mn>100</mn></mfrac><mo>=</mo><mfrac><mn>1</mn><mn>5</mn></mfrac></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true}</annotation></semantics></math>’ height=”47″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2247%22%20width%3D%2270%22%20wrs%3Abaseline%3D%2230%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmfrac%3E%3Cmn%3E20%3C%2Fmn%3E%3Cmn%3E100%3C%2Fmn%3E%3C%2Fmfrac%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmfrac%3E%3Cmn%3E1%3C%2Fmn%3E%3Cmn%3E5%3C%2Fmn%3E%3C%2Fmfrac%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math17f39f8317fbdb1988ef4c628eb’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADRjdnQgDVUNBwAAAVAAAAA6Z2x5ZoPi2VsAAAGMAAAAsmhlYWQQC2qxAAACQAAAADZoaGVhCGsXSAAAAngAAAAkaG10eE2rRkcAAAKcAAAACGxvY2EAHTwYAAA

Statistics Gcse Edexcel Higher