Cumulative-Frequency-Charts gcse Edexcel

Cumulative Frequency

What is cumulative frequency?

• Cumulative refers to a “running total” or “adding up as you go along”

• So in a table of grouped data

  • cumulative frequency means all of the frequencies for the different groups totalled up to the end of the group in a given row

• When working out cumulative frequencies you may see tables presented in two ways

  • A regular grouped data table with an extra column for cumulative frequencies

    • e.g. rows labelled 0 ≤ x < 20, 20 ≤ x < 40, 40 ≤ x < 60, etc

      	frequency	cumulative frequency
      0 ≤ x < 20	14	14
      20 ≤ x < 40	25	39 (because 14+25=39)
      40 ≤ x < 60	29	68 (because 14+25+29=68)
      60 ≤ x < 80	12	80 (because 14+25+29+12=80)

  • or a separate table where every group is relabelled as starting at the beginning (often zero)

    • e.g. rows labelled 0 ≤ x < 20, 0 ≤ x < 40, 0 ≤ x < 60, etc.

    • or x < 20, x < 40, x < 60, etc.

      	cumulative frequency
      0 ≤ x < 20 (or x < 20)	14
      0 ≤ x < 40 (or x < 40)	39
      0 ≤ x < 60 (or x < 60)	68
      0 ≤ x < 80 (or x < 80)	80

  • In the second type of table, you can subtract to find the individual frequencies

    • e.g. the frequency of the 20 ≤ x < 40 class interval is 39-14=25

    • the frequency of the 40 ≤ x < 60 class interval is 68-39=29

    • etc.

Cumulative Frequency Step Polygons

What is a cumulative frequency step polygon?

• A cumulative frequency step polygon is a way of representing discrete data

  • For grouped continuous data a cumulative frequency diagram would be used instead

How do I draw a cumulative frequency step polygon?

• This is best explained with an example

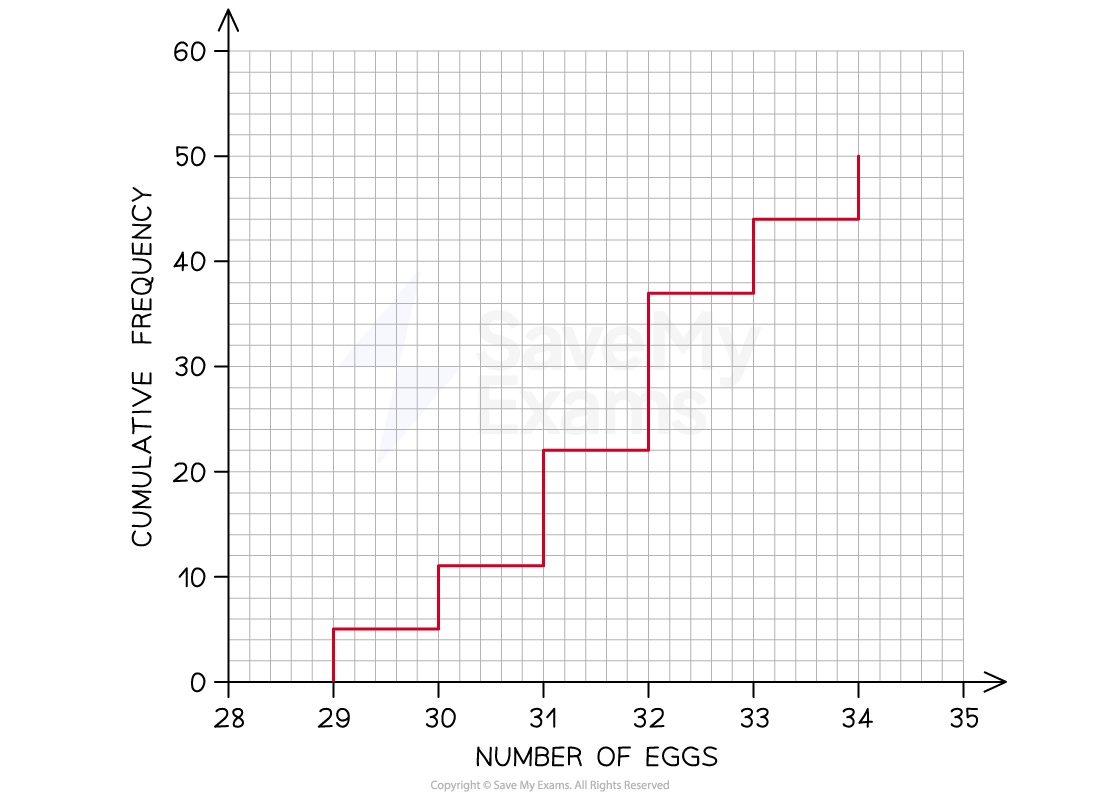
  • The numbers of eggs found in each nest in a survey of 50 American alligator nests are shown in the table below:

    Number of eggs	Frequency
    29	5
    30	6
    31	11
    32	15
    33	7
    34	6
    Total	50

  • Then the cumulative frequency is the running total of the frequencies

    Number of eggs	Frequency	Cumulative Frequency
    29	5	5
    30	6	5 + 6 = 11
    31	11	11 + 11 = 22
    32	15	22 + 15 = 37
    33	7	37 + 7 = 44
    34	6	44 + 6 = 50
    Total	50

• We can now draw the cumulative frequency step polygon

  • The cumulative frequency will always go on the vertical axis

    • The values in the data set will appear along the horizontal axis

  • The cumulative frequency is zero until we get to 29 eggs

    • So start at the point (29, 0)

  • Then the cumulative frequency jumps up to 5

    • Draw a vertical line from (29, 0) to (29, 5) to show this jump

  • Nothing changes until we get to 30 eggs

    • Draw a horizontal line from (29, 5) to (30, 5) to show this

  • At 30 eggs the cumulative frequency jumps up to 11

    • Draw a vertical line from (30, 5) to (30, 11) to show this jump

  • Continue the same way through the rest of the values in the table

    • The graph will end at the point (34, 50)

• Here is the final cumulative frequency diagram for the numbers of eggs

Cumulative Frequency Diagrams

What is a cumulative frequency diagram?

• A cumulative frequency diagram is a way of representing grouped continuous data

  • For discrete data a cumulative frequency step polygon would be used instead

• A cumulative frequency diagram can be used to estimate other statistical values

  • For example the median, quartiles or percentiles

How do I draw a cumulative frequency diagram?

• This is best explained with an example

  • The times taken to complete a short general knowledge quiz taken by 50 students are shown in the table below:

    Time taken ( seconds)	Frequency
    	3
    <img alt=”30 less or equal than s less than 35″ data-mathml='<math ><semantics><mrow><mn>30</mn><mo>≤</mo><mi>s</mi><mo>&lt;</mo><mn>35</mn></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true}</annotation></semantics></math>’ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2222%22%20width%3D%2277%22%20wrs%3Abaseline%3D%2216%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmn%3E30%3C%2Fmn%3E%3Cmo%3E%26%23×2264%3B%3C%2Fmo%3E%3Cmi%3Es%3C%2Fmi%3E%3Cmo%3E%26lt%3B%3C%2Fmo%3E%3Cmn%3E35%3C%2Fmn%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math1d3114856d6c6df443e3168d768’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAABNWhlYWQQC2qxAAACzAAAADZoaGVhCGsXSAAAAwQAAAAkaG10eE2rRkcAAAMoAAAADGxvY2EAHTwYAAADNAAAABBtYXhwBT0FPgAAA0QAAAAgbmFtZaBxlY4AAANkAAABn3Bvc3QB9wD6AAAFBAAAACBwcmVwa1uragAABSQAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACADwiZP%2F%2FAAAAPCJk%2F%2F%2F%2Fxd2eAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgABVAoACqwAFAAsAbBiwQRoAsQAAExCxAAbksQABExCwCTyxAQX1sAo8sAAQsQUD9bECBe2xBAP1sQMF7bAKELELA%2FWxCAXtsQYD9bEHBe0BsAwQsQED9rIJAAo8PDyxBQT1sgIICzw8PLEEBPWyBgcDPDw8sQ0D5hMHBRc1JwE1DQEXN4EBAQD%2F%2FwEA%2FwD%2FAAH%2FAatWgIBWgAEqVoCAVoAAAwCA%2F6sCgAKrAAMABwALAC8YAQCxCQA%2FsQgF5LECBfSxAQT0sQYF9LEDBOSxBQT0sQQF9LEHARA8sQA