Enlargements Wjec-Eduqas Foundation

课 Progress

0% Complete

Exam code:C300

Enlargements

What is an enlargement?

An enlargement changes the size and position of a shape
The length of each side of the shape is multiplied by a scale factor
- If the scale factor is greater than 1 then the enlarged image will be bigger than the original object
- If the scale factor is less than 1 then the enlarged image will be smaller than the original object
The centre of enlargement determines the position of the enlarged image
- If the scale factor is greater than 1 then the enlarged image will be further away from the centre of enlargement
- If the scale factor is less than 1 then the enlarged image will be closer to the centre of enlargement

How do I enlarge a shape?

STEP 1

Pick a vertex of the shape and count the horizontal and vertical distances from the centre of enlargement
STEP 2
Multiply both the horizontal and vertical distances by the given scale factor
STEP 3
Start at the centre of enlargement and measure the new distances to find the enlarged vertex
STEP 4
Repeat the steps for the other vertices
- You might be able to draw the enlarged shape from the first vertex by multiplying the original lengths by the scale factor
  - This can be done quickly if the shape is made up of vertical and horizontal lines
STEP 5
Connect the vertices on the enlarged image and label it

How do I describe an enlargement?

To describe an enlargement, you must:
- State that the transformation is an enlargement
- State the scale factor
- Give the coordinates of the centre of enlargement
To find the scale factor:
- Pick a side of the original shape
- Identify the corresponding side on the enlarged image
- Divide the length of the enlarged side by the length of the original side
To find the centre of enlargement:
- Pick a vertex of the original shape
- Identify the corresponding vertex on the enlarged image
- Draw a line going through these two vertices
- Repeat this for the other vertices of the original shape
- These lines will intersect at the centre of enlargement

How do I reverse an enlargement?

If a shape has been enlarged, you can perform a single transformation to return the shape to its original size and position
An enlargement can be reversed by multiplying the enlarged shape by the reciprocal of the original scale factor
- The centre of enlargement is the same
For a shape enlarged by a scale factor of 3 with centre of enlargement (-1, 6)
- The reverse transformation is
  - an enlargement of scale factor $1 third$
  - with centre of enlargement (-1, 6)

Examiner Tips and Tricks

To check that you have enlarged a shape correctly:
- Draw lines going from the centre of enlargement to each of the vertices of the original shape
- Extend these lines
- The lines should go through the corresponding vertices of the enlarged image

Worked Example

(a) On the grid below enlarge shape C using scale factor 2 and centre of enlargement (2, 1).

Label your enlarged shape C’.

Enlargement-Q1, IGCSE & GCSE Maths revision notes

Start by marking on the centre of enlargement (CoE).
Count the number of squares in both a horizontal and vertical direction to go from the CoE to one of the vertices on the original object, this is 2 to the right and 3 up in this example.
As the scale factor is 2, multiply these distances by 2, so they become 4 to the right and 6 up.
Count these new distances from the CoE to the corresponding point on the enlarged image and mark it on.
Draw a line through the CoE and the pair of corresponding points, they should line up in a straight line.

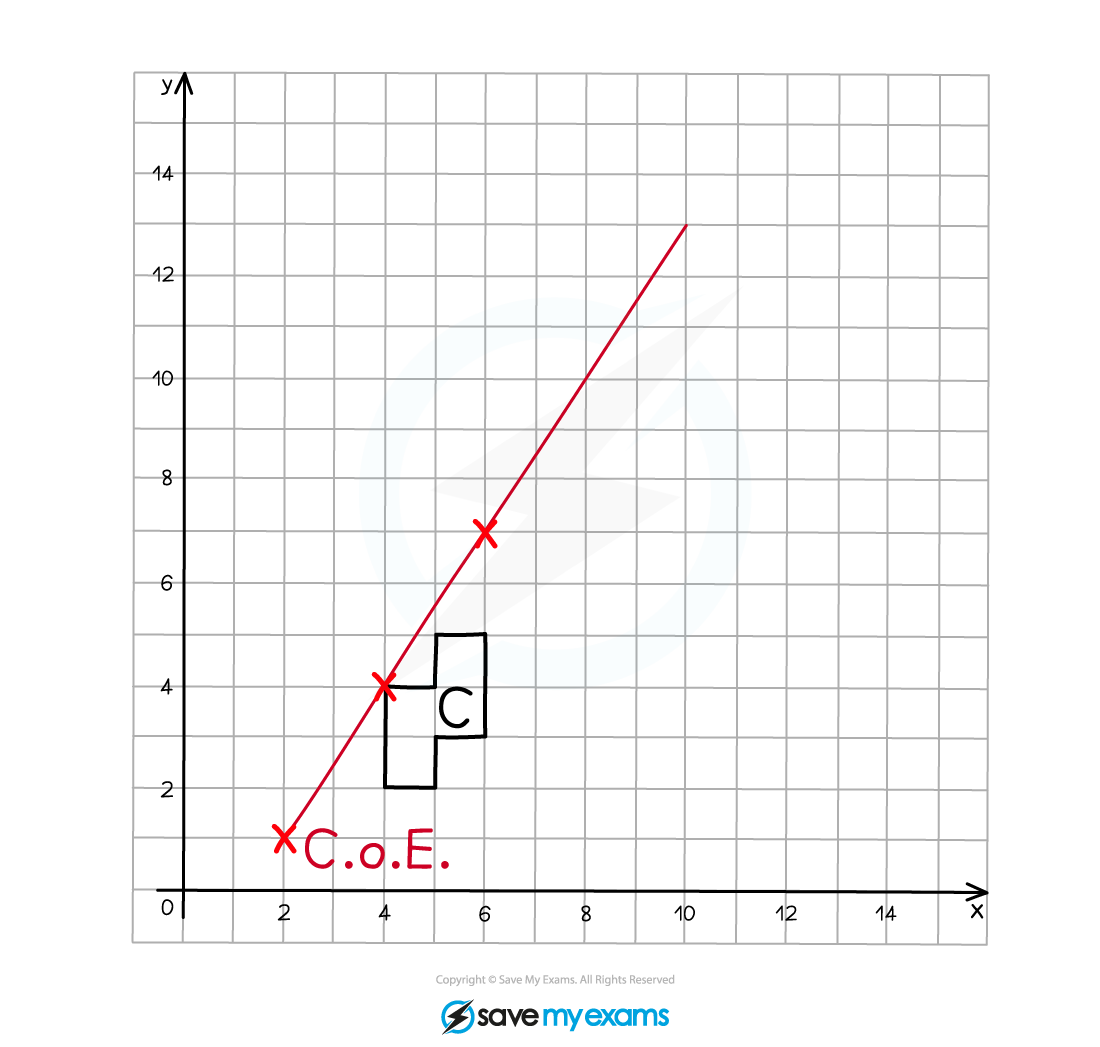
Enlargement-Q1-working, IGCSE & GCSE Maths revision notes

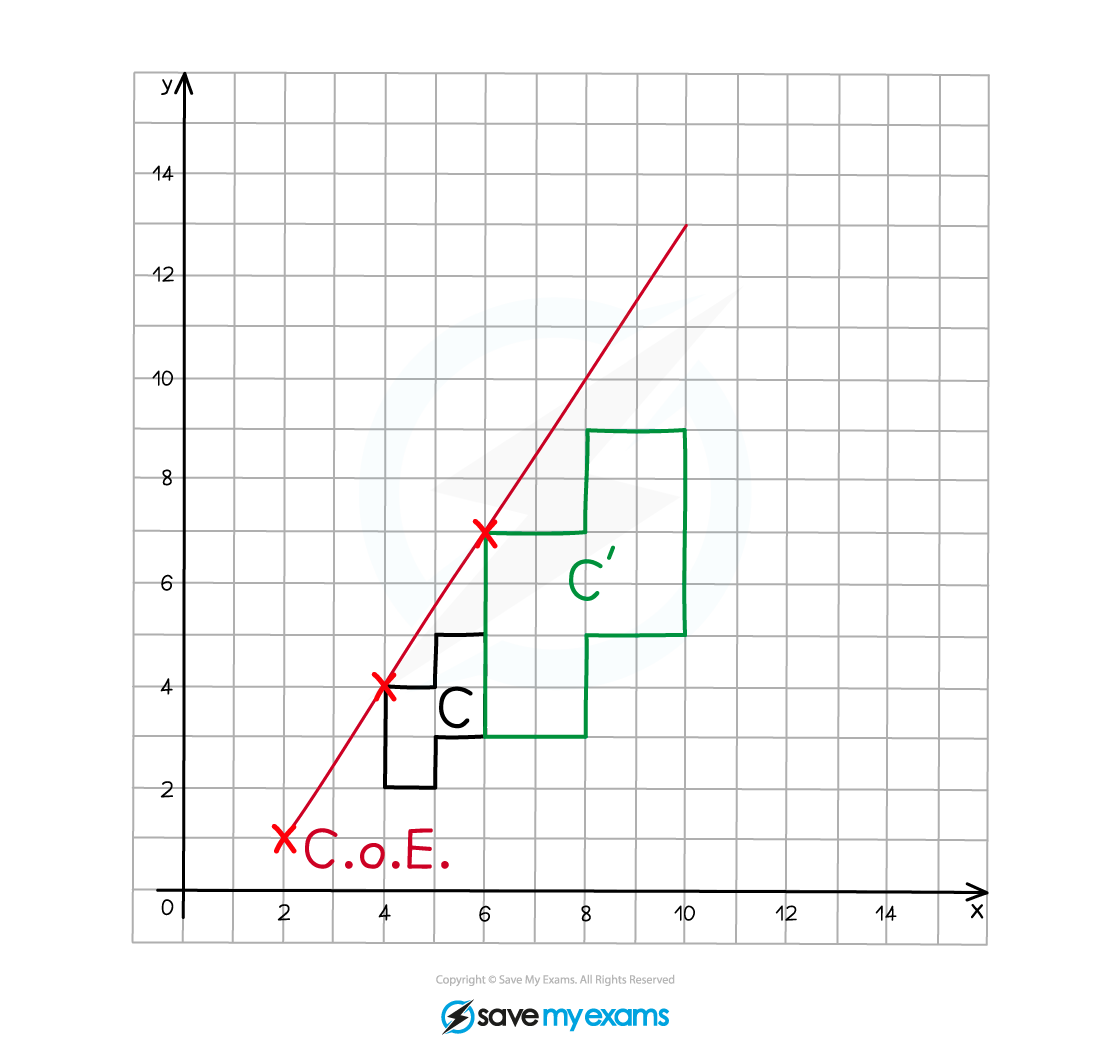
Repeat this process for each of the vertices on the original object (or at least 2).
Join adjacent vertices on the enlarged image as you go.
Label the enlarged image C’.

Enlargement-Q1-Final-Answer, IGCSE & GCSE Maths revision notes

(b) Describe fully the single transformation that creates shape B from shape A.

Enlargement-Q2, IGCSE & GCSE Maths revision notes

We can see that the image is larger than the original object, therefore it must be an enlargement.
As the enlarged image is bigger than the original object, the scale factor must be greater than 1.
Compare two corresponding edges on the object and the image to find the scale factor.

The height of the original “H” is 3 squares
The height of the enlarged “H” is 9 squares

<img alt=”therefore Scale space Factor space equals 9 over 3 equals 3″ data-mathml='<math ><semantics><mrow><mo >∴</mo><mi >Scale</mi><mo > </mo><mi >Factor</mi><mo > </mo><mo >=</mo><mfrac ><mn>9</mn><mn>3</mn></mfrac><mo >=</mo><mn >3</mn></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true}</annotation></semantics></math>’ data-type=”working” height=”47″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2247%22%20width%3D%22171%22%20wrs%3Abaseline%3D%2230%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23×2234%3B%3C%2Fmo%3E%3Cmi%20mathcolor%3D%22%23000000%22%3EScale%3C%2Fmi%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%20mathcolor%3D%22%23000000%22%3EFactor%3C%2Fmi%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%3D%3C%2Fmo%3E%3Cmfrac%20mathcolor%3D%22%23000000%22%3E%3Cmn%3E9%3C%2Fmn%3E%3Cmn%3E3%3C%2Fmn%3E%3C%2Fmfrac%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%3D%3C%2Fmo%3E%3Cmn%20mathcolor%3D%22%23000000%22%3E3%3C%2Fmn%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math1f0b57a9ccae93e289fb2a26cc8’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAABL2hlYWQQC2qxAAACxAAAADZoaGVhCGsXSAAAAvwAAAAkaG10eE2rRkcAAAMgAAAADGxvY2EAHTwYAAADLAAAABBtYXhwBT0FPgAAAzwAAAAgbmFtZaBxlY4AAANcAAABn3Bvc3QB9wD6AAAE%2FAAAACBwcmVwa1uragAABRwAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0iNP%2F%2FAAAAPSI0%2F%2F%2F%2FxN3OAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAMAbAArAusCQAADAAcACwBNGAGwDBCwBNSwBBCwBtSwBBCwAtSwAhCwANSwBRCwC9SwCxCwCdQAsAwQsAfUsAcQsAXUsAcQsALUsAIQsADUsAIQsAs8sAAQsAg8MDE3MzUjATM1IxMzNSNsgIABAICA%2F4CAK4ABFYD964AAAAEAAAABAADVeM5BXw889QADBAD%2F%2F%2F%2F%2F1joTc%2F%2F%2F%2F%2F%2FWOhNzAAD%2FIASAA6sAAAAKAAIAAQAAAAAAAQAAA%2Bj%2FagAAF3AAAP%2B2BIAAAQAAAAAAAAAAAAAAAAAAAAMDUgBVA1YAgANVAGwAAAAAAAAAKAAAALIAAAEvAAEAAAADAF4ABQAAAAAAAgCABAAAAAAABAAA3gAAAAAAAAAVAQIAAAAAAAAAAQASAAAAAAAAAAAAAgAOABIAAAAAAAAAAwAwACAAAAAAAAAABAASAFAAAAAAAAAABQAWAGIAAAAAAAAABgAJAHgAAAAAAAAACAAcAIEAAQAAAAAAAQASAAAAAQAAAAAAAgAOABIAAQAAAAAAAwAwACAAAQAAAAAABAASAFAAAQAAAAAABQAWAGIAAQAAAAAABgAJAHgAAQAAAAAACAAcAIEAAwABBAkAAQASAAAAAwABBAkAAgAOABIAAwABBAkAAwAwACAAAwABBAkABAASAFAAAwABBAkABQAWAGIAAwABBAkABgAJAHgAAwABBAkACAAcAIEATQBhAHQAaAAgAEYAb

Maths Gcse Wjec-Eduqas Foundation