Problem-Solving-With-Volumes Edexcel Higher

课 Progress

0% Complete

Exam code:1MA1

Problem-solving with volumes

What is problem-solving?

Problem-solving, usually has two key features:
- A question is given as a real-life scenario
  - eg. The volume of water in a swimming pool…
- There is usually more than one topic of maths you will need in order to answer the question
  - eg. Volume and money

What are common problems that involve volume?

Volume is a commonly used topic of ‘real-world’ maths
- For example, a carton of juice in the shape of a cuboid, a cylindrical tin and a triangular prism chocolate box all involve volume
Typically, the ‘real-world’ scenarios also have a cost
- A lot of volume problems also involve calculations with money

How do I solve problems involving volume?

Often the 3D object in a question will not be a standard cuboid, cone, sphere, etc.
- It will likely either be:
  - A prism (3D shape with the same cross-section running through it)
  - A portion or fraction of a standard shape (a hemisphere for example)
  - A compound object (an object made up of two or more standard 3D objects)
If the object is a prism, recall that the volume of a prism is the cross-sectional area × its length
- The cross-sectional area may be a compound 2D shape
  - For example, an L-shape, or a combination of a rectangle and a triangle
If the object is a fraction of a standard shape, consider the “full” version of the object and find the appropriate fraction of it
- A hemisphere is half a sphere
- A frustum is a truncated (chopped-off) cone or pyramid
  - The volume of a frustum will be the volume of the smaller cone or pyramid subtracted from the volume of the larger cone or pyramid
If the object is a compound object, find the volumes of the individual standard 3D objects and add them together

Problem solving questions could appear on either a non-calculator paper or a calculator paper

Examiner Tips and Tricks

Before you start calculating, make a quick note of your plan to tackle the question
- For example, “Find the area of the triangle and the rectangle, add together, multiply by the length”

Worked Example

The diagram shows a prism.

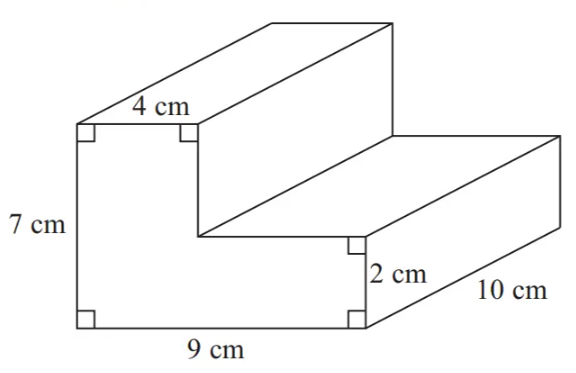
Work out the volume of the prism.

The volume is the area of the cross section × length (10 cm)
Find the area by splitting into a 7 × 4 and a (9 – 4) × 2 rectangle (or a 9 × 2 and a (7 – 2) × 4 rectangle)

7 × 4 + (9 – 4) × 2 = 38 cm²

Find the volume (by multiplying 38 by 10)

38 × 10

380 cm³

Worked Example

The diagram shows a truncated cone (a frustum).
Using the given dimensions, find the volume of the frustum to 3 significant figures.

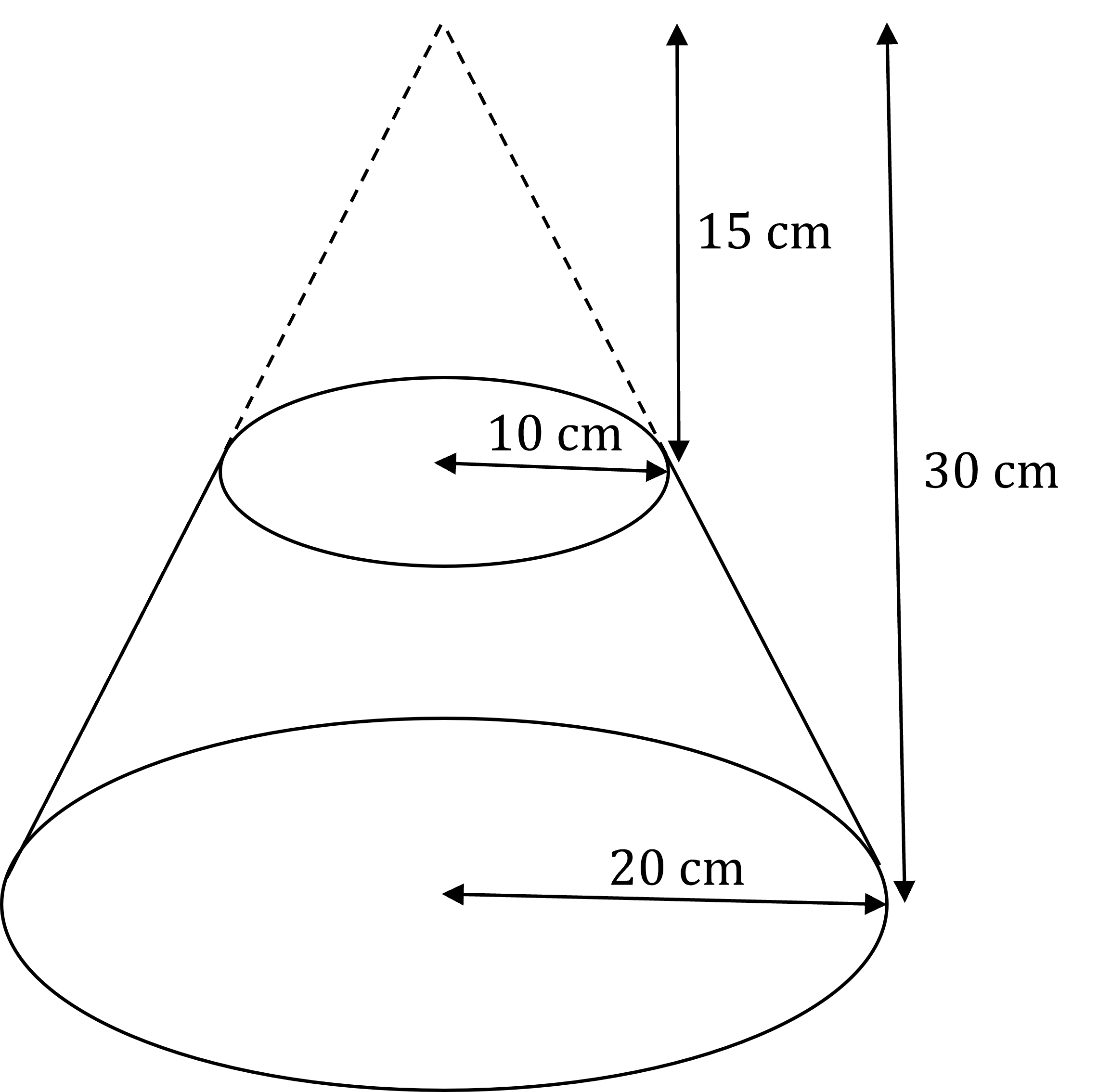
To find the volume of the frustum, find the volume of the larger cone (30 cm tall, with a radius of 20 cm), and subtract the volume of the smaller cone (15 cm tall, with a radius of 10 cm)

Formula for the volume of a cone: $1 third pi space r squared straight h$

Calculate the volume of the larger cone

<img alt=”V subscript L equals 1 third cross times pi cross times 20 squared cross times 30 equals 4000 pi equals 12 space 566.37061… space cm cubed” data-mathml=”<math ><semantics><mrow><msub><mi>V</mi><mi>L</mi></msub><mo>=</mo><mfrac><mn>1</mn><mn>3</mn></mfrac><mo>×</mo><mi>π</mi><mo>×</mo><msup><mn>20</mn><mn>2</mn></msup><mo>×</mo><mn>30</mn><mo>=</mo><mn>4000</mn><mi>π</mi><mo>=</mo><mn>12</mn><mo> </mo><mn>566</mn><mo>.</mo><mn>37061</mn><mo>.</mo><mo>.</mo><mo>.</mo><mo> </mo><msup><mi>cm</mi><mn>3</mn></msup></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true,”toolbar”:”<toolbar ref=’general’><tab ref=’general’><removeItem ref=’setColor’/><removeItem ref=’bold’/><removeItem ref=’italic’/><removeItem ref=’autoItalic’/><removeItem ref=’setUnicode’/><removeItem ref=’mtext’ /><removeItem ref=’rtl’/><removeItem ref=’forceLigature’/><removeItem ref=’setFontFamily’ /><removeItem ref=’setFontSize’/></tab></toolbar>”}</annotation></semantics></math>” data-type=”working” height=”47″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2247%22%20width%3D%22395%22%20wrs%3Abaseline%3D%2230%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmsub%3E%3Cmi%3EV%3C%2Fmi%3E%3Cmi%3EL%3C%2Fmi%3E%3C%2Fmsub%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmfrac%3E%3Cmn%3E1%3C%2Fmn%3E%3Cmn%3E3%3C%2Fmn%3E%3C%2Fmfrac%3E%3Cmo%3E%26%23xD7%3B%3C%2Fmo%3E%3Cmi%3E%26%23x3C0%3B%3C%2Fmi%3E%3Cmo%3E%26%23xD7%3B%3C%2Fmo%3E%3Cmsup%3E%3Cmn%3E20%3C%2Fmn%3E%3Cmn%3E2%3C%2Fmn%3E%3C%2Fmsup%3E%3Cmo%3E%26%23xD7%3B%3C%2Fmo%3E%3Cmn%3E30%3C%2Fmn%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmn%3E4000%3C%2Fmn%3E%3Cmi%3E%26%23x3C0%3B%3C%2Fmi%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmn%3E12%3C%2Fmn%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmn%3E566%3C%2Fmn%3E%3Cmo%3E.%3C%2Fmo%3E%3Cmn%3E37061%3C%2Fmn%3E%3Cmo%3E.%3C%2Fmo%3E%3Cmo%3E.%3C%2Fmo%3E%3Cmo%3E.%3C%2Fmo%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmsup%3E%3Cmi%3Ecm%3C%2Fmi%3E%3Cmn%3E3%3C%2Fmn%3E%3C%2Fmsup%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math1582077ca2086af98e358c1d1a2’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAAExjdnQgDVUNBwAAAWgAAAA6Z2x5ZoPi2VsAAAGkAAAB9mhlYWQQC2qxAAADnAAAADZoaGVhCGsXSAAAA9QAAAAkaG10eE2rRkcAAAP4AAAAFGxvY2EAHTwYAAAEDAAAABhtYXhwBT0FPgAABCQAAAAgbmFtZaBxlY4AAAREAAABn3Bvc3QB9wD6AAAF5AAAACBwcmVwa1uragAABgQAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEADgAAAAKAAgAAgACAC4APQDXA8D%2F%2FwAAAC4APQDXA8D%2F%2F%2F%2FT%2F8X%2FLPxEAAEAAAAAAAAAAAAAAAABVAMsAIABAABWACoCWAIeAQ4BLAIsAFoBgAKAAKAA1ACAAAAAAAAAACsAVQCAAKsA1QEAASsABwAAAAIAVQAAAwADqwADAAcAADMRIRElIREhVQKr%2FasCAP4AA6v8VVUDAAABACAAAACgAIAAAwAvGAGwBBCwA9SwAxCwAtSwAxCwADywAhCwATwAsAQQsAPUsAMQsAI8sAAQsAE8MDE3MxUjIICAgIAAAgCAAOsC1QIVAAMABwBlGAGwCBCwBtSwBhCwBdSwCBCwAdSwARCwANSwBhCwBzywBRCwBDywARCwAjywABCwAzwAsAgQsAbUsAYQsAfUsAcQsAHUsAEQsALUsAYQsAU8sAcQsAQ8sAEQsAA8sAIQsAM8MTATITUhHQEhNYACVf2rAlUBwFXVVVUAAgCAAFUC1QKAAAMABwBGGLABFACxAAATELEACeSxAAETELAEPLEGCPSwAjwwAbEIARMQsQAD9rAHPLEBBfWwBjyyBQcAEPSwAjyxCQPmsQQF9bADPBMzASMRMwEjgFUCAFVV%2FgBVAoD91QIr%2FdUAAQBVAAACwAJAABkAQRgBsBoQsA3UsA0QsAfUsAcQsATUsAQQsBjUALAaELAL1LAaELAC1LAaELAP1LAPELAU1LAPELAGPLAPELAXPDAxJQYjIjUDIxEUBisBNjU0JyIVIzQzIRUjExQCwBVAgAGqKQFVKgFVQGoCAYEBVVXVARb%2B6pVAQJWAliuAVf7qwAAAAAEAAAABAADVeM5BXw889QADBAD%2F%2F%2F%2F%2F1joTc%2F%2F%2F%2F%2F%2FWOhNzAAD%2FIASAA6sAAAAKAAIAAQAAAAAAAQAAA%2Bj%2FagAAF3AAAP%2B2BIAAAQAAAAAAAAAAAAAAAAAAAAUDUgBVAMgAIANWAIADVgCAAxYAVQAAAAAAAAAoAAAAbgAAAPgAAAFnAAAB9gABAAAABQBeAAUAAAAAAAIAgAQAAAAAAAQAAN4AAAAAAAAAFQECAAAAAAAAAAEAEgAAAAAAAAAAAAIADgASAAAAAAAAAAMAMAAgAAAAAAAAAAQAEgBQAAAAAAAAAAUAFgBiAAAAAAAAAAYACQB4AAAAAAAAAAgAHACBAAEAAAAAAAEAEgAAAAEAAAAAAAIADgASAAEAAAAAAAMAMAAgAAEAAAAAAAQAEgBQAAEAAAAAAAUAFgBiAAEAAAAAAAYACQB4AAEAAAAAAAgAHACBAAMAAQQJAAEAEgAAAAMAAQQJAAIADgASAAMAAQQJAAMAMAAgAAMAAQQJAAQAEgBQAAMAAQQJAAUAFgBiAAMAAQQJAAYACQB4AAMAAQQJAAgAHACBAE0AYQB0AGgAIABGAG8AbgB0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAATQBhAHQAaAAgAEYAbwBuAHQATQBhAHQAaAAgAEYAbwBuAHQAVgBlAHIAcwBpAG8AbgAgADEALgAwTWF0aF9Gb250AE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAAAwAAAAAAAAH0APoAAAAAAAAAAAAAAAAAAAAAAAAAALkHEQAAjYUYALIAAAAVFBOxAAE%2F)format(‘truetype’)%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%226.5%22%20y%3D%2230%22%3EV%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2213%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2218.5%22%20y%3D%2238%22%3EL%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2231.5%22%20y%3D%2230%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20×1%3D%2242.5%22%20×2%3D%2254.5%22%20y1%3D%2223.5%22%20y2%3D%2223.5%22%2F%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2248.5%22%20y%3D%2216%22%3E1%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2248.5%22%20y%3D%2241%22%3E3%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2265.5%22%20y%3D%2230%22%3E%26%23xD7%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2280.5%22%20y%3D%2230%22%3E%26%23x3C0%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2295.5%22%20y%3D%2230%22%3E%26%23xD7%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22113.5%22%20y%3D%2230%22%3E20%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2213%22%20text-anchor%3D%22middle%22%20x%3D%22125.5%22%20y%3D%2225%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22137.5%22%20y%3D%2230%22%3E%26%23xD7%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22155.5%22%20y%3D%2230%22%3E30%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22172.5%22%20y%3D%2230%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22199.5%22%20y%3D%2230%22%3E4000%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22223.5%22%20y%3D%2230%22%3E%26%23x3C0%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22238.5%22%20y%3D%2230%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22256.5%22%20y%3D%2230%22%3E12%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22282.5%22%20y%3D%2230%22%3E566%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22298.5%22%20y%3D%2230%22%3E.%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22323.5%22%20y%3D%2230%22%3E37061%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22348.5%22%20y%3D%2230%22%3E.%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22353.5%22%20y%3D%2230%22%3E.%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1582077ca2086af98e358c1d1a2%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22358.5%22%20y

Maths Gcse Edexcel Higher

Problem-Solving-With-Volumes Edexcel Higher