WEILAI Online Academic assistant
WEILAI Online Academic assistant
Back to 课程

Maths Gcse Edexcel Higher

0% Complete
0/0 Steps
  1. Scatter-Graphs-And-Correlation Edexcel Higher
    2 主题
  2. Cumulative-Frequency-And-Box-Plots Edexcel Higher
    4 主题
  3. Histograms Edexcel Higher
    3 主题
  4. Statistical-Diagrams Edexcel Higher
    7 主题
  5. Averages-Ranges-And-Data Edexcel Higher
    8 主题
  6. Combined-And-Conditional-Probability Edexcel Higher
    3 主题
  7. Tree-Diagrams Edexcel Higher
    1 主题
  8. Simple-Probability-Diagrams Edexcel Higher
    3 主题
  9. Transformations Edexcel Higher
    5 主题
  10. Vectors Edexcel Higher
    6 主题
  11. 3D-Pythagoras-And-Trigonometry Edexcel Higher
    1 主题
  12. Sine-Cosine-Rule-And-Area-Of-Triangles Edexcel Higher
    4 主题
  13. Pythagoras-And-Trigonometry Edexcel Higher
    4 主题
  14. Area-And-Volume-Of-Similar-Shapes Edexcel Higher
    1 主题
  15. Congruence-Similarity-And-Geometrical-Proof Edexcel Higher
    5 主题
  16. Volume-And-Surface-Area Edexcel Higher
    3 主题
  17. Circles-Arcs-And-Sectors Edexcel Higher
    2 主题
  18. Area-And-Perimeter Edexcel Higher
    4 主题
  19. Circle-Theorems Edexcel Higher
    7 主题
  20. Bearings-Scale-Drawing-Constructions-And-Loci Edexcel Higher
    5 主题
  21. Angles-In-Polygons-And-Parallel-Lines Edexcel Higher
    3 主题
  22. Symmetry-And-Shapes Edexcel Higher
    6 主题
  23. Exchange-Rates-And-Best-Buys Edexcel Higher
    2 主题
  24. Standard-And-Compound-Units Edexcel Higher
    5 主题
  25. Direct-And-Inverse-Proportion Edexcel Higher
    2 主题
  26. Problem-Solving-With-Ratios Edexcel Higher
    2 主题
  27. Ratios Edexcel Higher
    3 主题
  28. Sequences Edexcel Higher
    4 主题
  29. Transformations-Of-Graphs Edexcel Higher
    2 主题
  30. Graphing-Inequalities Edexcel Higher
    2 主题
  31. Solving-Inequalities Edexcel Higher
    2 主题
  32. Real-Life-Graphs Edexcel Higher
    4 主题
  33. Estimating-Gradients-And-Areas-Under-Graphs Edexcel Higher
    2 主题
  34. Equation-Of-A-Circle Edexcel Higher
    2 主题
  35. Graphs-Of-Functions Edexcel Higher
    6 主题
  36. Linear-Graphs Edexcel Higher
    4 主题
  37. Coordinate-Geometry Edexcel Higher
    4 主题
  38. Functions Edexcel Higher
    3 主题
  39. Forming-And-Solving-Equations Edexcel Higher
    3 主题
  40. Iteration Edexcel Higher
    1 主题
  41. Simultaneous-Equations Edexcel Higher
    2 主题
  42. Quadratic-Equations Edexcel Higher
    4 主题
  43. Linear-Equations Edexcel Higher
    1 主题
  44. Algebraic-Proof Edexcel Higher
    1 主题
  45. Rearranging-Formulas Edexcel Higher
    2 主题
  46. Algebraic-Fractions Edexcel Higher
    4 主题
  47. Completing-The-Square Edexcel Higher
    1 主题
  48. Factorising Edexcel Higher
    6 主题
  49. Expanding-Brackets Edexcel Higher
    3 主题
  50. Algebraic-Roots-And-Indices Edexcel Higher
    1 主题
  51. Introduction Edexcel Higher
    7 主题
  52. Using-A-Calculator Edexcel Higher
    1 主题
  53. Surds Edexcel Higher
    2 主题
  54. Rounding-Estimation-And-Bounds Edexcel Higher
    2 主题
  55. Fractions-Decimals-And-Percentages Edexcel Higher
    3 主题
  56. Simple-And-Compound-Interest-Growth-And-Decay Edexcel Higher
    4 主题
  57. Percentages Edexcel Higher
    3 主题
  58. Fractions Edexcel Higher
    4 主题
  59. Powers-Roots-And-Standard-Form Edexcel Higher
    4 主题
  60. Prime-Factors-Hcf-And-Lcm Edexcel Higher
    4 主题
  61. Number-Operations Edexcel Higher
    10 主题
课 Progress
0% Complete

Exam code:1MA1

Enlargements

What is an enlargement?

  • An enlargement changes the size and position of a shape

  • The length of each side of the shape is multiplied by a scale factor

    • If the scale factor is greater than 1 then the enlarged image will be bigger than the original object

    • If the scale factor is between 0 and 1 (fractional) then the enlarged image will be smaller than the original object

  • The centre of enlargement determines the position of the enlarged image

    • If the scale factor is greater than 1 then the enlarged image will be further away from the centre of enlargement

    • If the scale factor is between 0 and 1 then the enlarged image will be closer to the centre of enlargement

How do I enlarge a shape?

  • STEP 1

    Pick a vertex of the shape and count the horizontal and vertical distances from the centre of enlargement

  • STEP 2
    Multiply both the horizontal and vertical distances by the given scale factor

  • STEP 3
    Start at the centre of enlargement and measure the new distances to find the enlarged vertex

  • STEP 4
    Repeat the steps for the other vertices

    • You might be able to draw the enlarged shape from the first vertex by multiplying the original lengths by the scale factor

      • This can be done quickly if the shape is made up of vertical and horizontal lines

  • STEP 5
    Connect the vertices on the enlarged image and label it

How do I describe an enlargement?

  • To describe an enlargement, you must:

    • State that the transformation is an enlargement

    • State the scale factor

      • This may be an integer or a fraction

    • Give the coordinates of the centre of enlargement

  • To find the scale factor:

    • Pick a side of the original shape

    • Identify the corresponding side on the enlarged image

      • For a fractional enlargement, the side on the enlarged image will be smaller than the corresponding side on the original image

    • Divide the length of the enlarged side by the length of the original side

  • To find the centre of enlargement:

    • Pick a vertex of the original shape

    • Identify the corresponding vertex on the enlarged image

    • Draw a line going through these two vertices

    • Repeat this for the other vertices of the original shape

    • These lines will intersect at the centre of enlargement

How do I reverse an enlargement?

  • If a shape has been enlarged, you can perform a single transformation to return the shape to its original size and position

  • An enlargement can be reversed by multiplying the enlarged shape by the reciprocal of the original scale factor

    • The centre of enlargement is the same

  • For a shape enlarged by a scale factor of 3 with centre of enlargement (-1, 6)

    • The reverse transformation is

      • an enlargement of scale factor 1 third

      • with centre of enlargement (-1, 6)

Examiner Tips and Tricks

  • To check that you have enlarged a shape correctly:

    • Draw lines going from the centre of enlargement to each of the vertices of the original shape

    • Extend these lines

    • The lines should go through the corresponding vertices of the enlarged image

Worked Example

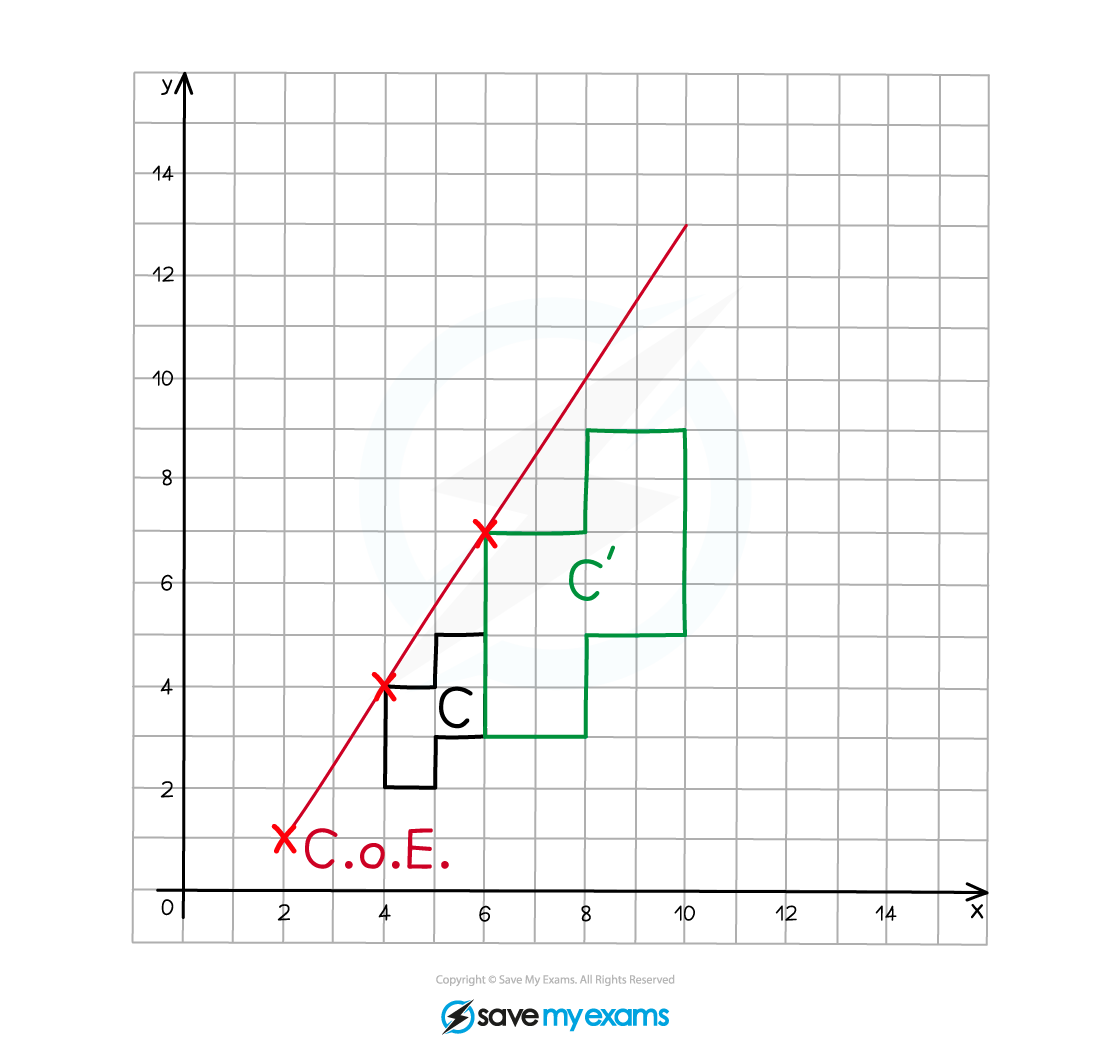
(a) On the grid below enlarge shape C using scale factor 2 and centre of enlargement (2, 1).

Label your enlarged shape C’.

An object labelled C with vertices at (4, 2), (4, 4), (5, 4), (5, 5), (6, 5), (6, 3), (5, 3) and (5, 2).

Start by marking on the centre of enlargement (CoE)

Count the number of squares in both a horizontal and vertical direction to go from the CoE to one of the vertices on the original object, this is 2 to the right and 3 up in this example

As the scale factor is 2, multiply these distances by 2, so they become 4 to the right and 6 up

Count these new distances from the CoE to the corresponding point on the enlarged image and mark it on

Draw a line through the CoE and the pair of corresponding points, they should line up in a straight line

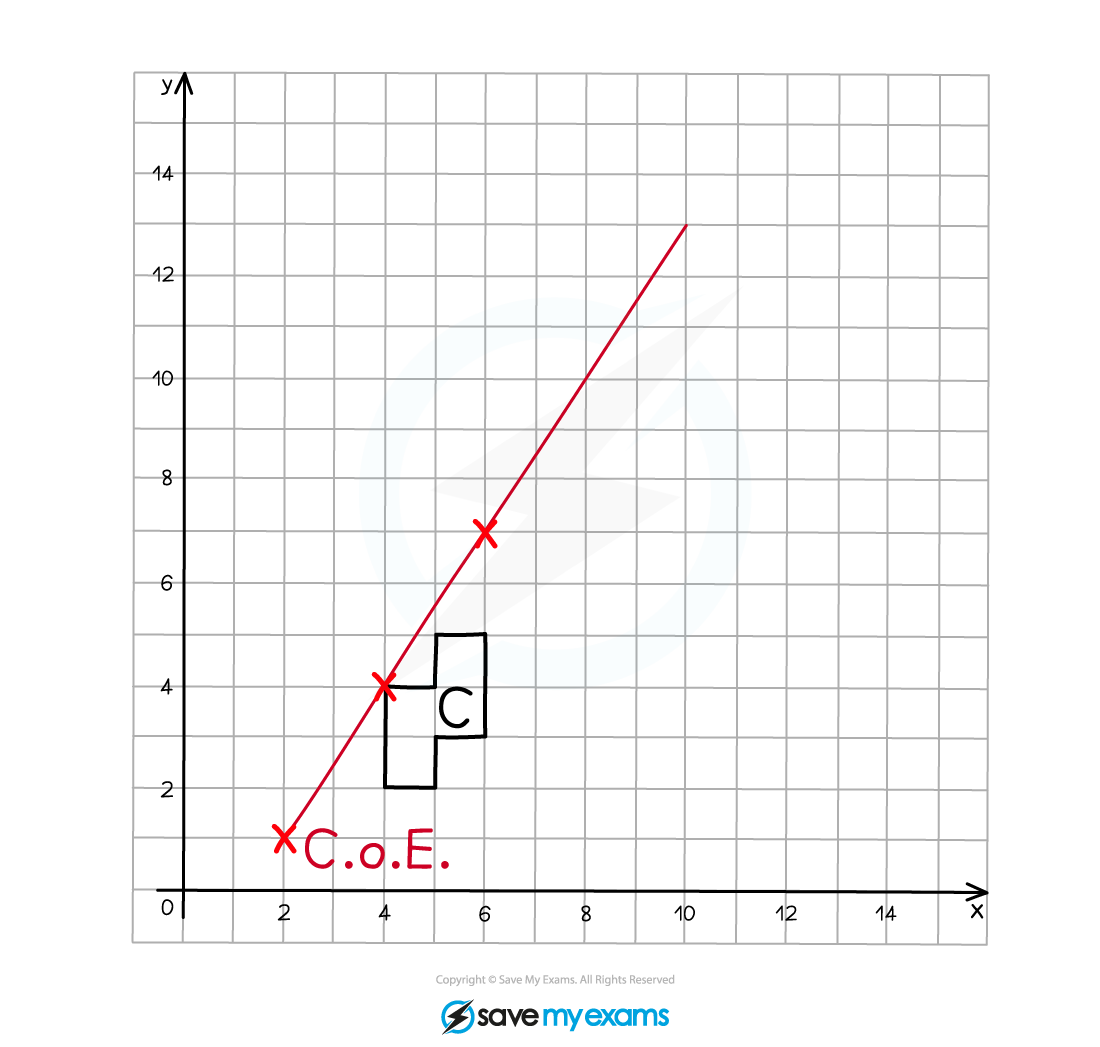
An object labelled C with the COE marked at (2, 1) and a line going through the COE and one vertex on the shape.

Repeat this process for each of the vertices on the original object (or at least 2)

Join adjacent vertices on the enlarged image as you go

Label the enlarged image C’

An object labelled C with the enlarged image (COE = (2, 1) and SF = 2) labelled C'.

(b) Describe fully the single transformation that creates shape B from shape A.

An H-shaped object labelled A and a larger H-shaped object marked B.

We can see that the image is larger than the original object, therefore it must be an enlargement

As the enlarged image is bigger than the original object, the scale factor must be greater than 1

Compare two corresponding edges on the object and the image to find the scale factor

The height of the original “H” is 3 squares
The height of the enlarged “H” is 9 squares

<img alt=”therefore Scale space Factor space equals 9 over 3 equals 3″ data-mathml='<math ><semantics><mrow><mo >∴</mo><mi >Scale</mi><mo > </mo><mi >Factor</mi><mo > </mo><mo >=</mo><mfrac ><mn>9</mn><mn>3</mn></mfrac><mo >=</mo><mn >3</mn></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true}</annotation></semantics></math>’ data-type=”working” height=”47″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2247%22%20width%3D%22171%22%20wrs%3Abaseline%3D%2230%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23×2234%3B%3C%2Fmo%3E%3Cmi%20mathcolor%3D%22%23000000%22%3EScale%3C%2Fmi%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%20mathcolor%3D%22%23000000%22%3EFactor%3C%2Fmi%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%3D%3C%2Fmo%3E%3Cmfrac%20mathcolor%3D%22%23000000%22%3E%3Cmn%3E9%3C%2Fmn%3E%3Cmn%3E3%3C%2Fmn%3E%3C%2Fmfrac%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%3D%3C%2Fmo%3E%3Cmn%20mathcolor%3D%22%23000000%22%3E3%3C%2Fmn%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math1f0b57a9ccae93e289fb2a26cc8’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAABL2hlYWQQC2qxAAACxAAAADZoaGVhCGsXSAAAAvwAAAAkaG10eE2rRkcAAAMgAAAADGxvY2EAHTwYAAADLAAAABBtYXhwBT0FPgAAAzwAAAAgbmFtZaBxlY4AAANcAAABn3Bvc3QB9wD6AAAE%2FAAAACBwcmVwa1uragAABRwAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0iNP%2F%2FAAAAPSI0%2F%2F%2F%2FxN3OAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAMAbAArAusCQAADAAcACwBNGAGwDBCwBNSwBBCwBtSwBBCwAtSwAhCwANSwBRCwC9SwCxCwCdQAsAwQsAfUsAcQsAXUsAcQsALUsAIQsADUsAIQsAs8sAAQsAg8MDE3MzUjATM1IxMzNSNsgIABAICA%2F4CAK4ABFYD964AAAAEAAAABAADVeM5BXw889QADBAD%2F%2F%2F%2F%2F1joTc%2F%2F%2F%2F%2F%2FWOhNzAAD%2FIASAA6sAAAAKAAIAAQAAAAAAAQAAA%2Bj%2FagAAF3AAAP%2B2BIAAAQAAAAAAAAAAAAAAAAAAAAMDUgBVA1YAgANVAGwAAAAAAAAAKAAAALIAAAEvAAEAAAADAF4ABQAAAAAAAgCABAAAAAAABA

Responses

您的邮箱地址不会被公开。 必填项已用 * 标注