Maths Gcse Edexcel Higher
-
Scatter-Graphs-And-Correlation Edexcel Higher2 主题
-
Cumulative-Frequency-And-Box-Plots Edexcel Higher4 主题
-
Histograms Edexcel Higher3 主题
-
Statistical-Diagrams Edexcel Higher7 主题
-
Averages-Ranges-And-Data Edexcel Higher8 主题
-
Capture-Recapture Edexcel Higher
-
Population-And-Sampling Edexcel Higher
-
Comparing-Data-Sets Edexcel Higher
-
Range-And-Interquartile-Range Edexcel Higher
-
Averages-From-Grouped-Data Edexcel Higher
-
Averages-From-Tables Edexcel Higher
-
Calculations-With-The-Mean Edexcel Higher
-
Mean-Median-And-Mode Edexcel Higher
-
Capture-Recapture Edexcel Higher
-
Combined-And-Conditional-Probability Edexcel Higher3 主题
-
Tree-Diagrams Edexcel Higher1 主题
-
Simple-Probability-Diagrams Edexcel Higher3 主题
-
Transformations Edexcel Higher5 主题
-
Vectors Edexcel Higher6 主题
-
3D-Pythagoras-And-Trigonometry Edexcel Higher1 主题
-
Sine-Cosine-Rule-And-Area-Of-Triangles Edexcel Higher4 主题
-
Pythagoras-And-Trigonometry Edexcel Higher4 主题
-
Area-And-Volume-Of-Similar-Shapes Edexcel Higher1 主题
-
Congruence-Similarity-And-Geometrical-Proof Edexcel Higher5 主题
-
Volume-And-Surface-Area Edexcel Higher3 主题
-
Circles-Arcs-And-Sectors Edexcel Higher2 主题
-
Area-And-Perimeter Edexcel Higher4 主题
-
Circle-Theorems Edexcel Higher7 主题
-
Circle-Theorem-Proofs Edexcel Higher
-
The-Alternate-Segment-Theorem Edexcel Higher
-
Angles-In-The-Same-Segment Edexcel Higher
-
Angles-In-Cyclic-Quadrilaterals Edexcel Higher
-
Theorems-With-Chords-And-Tangents Edexcel Higher
-
Angle-In-A-Semicircle Edexcel Higher
-
Angles-At-Centre-And-Circumference Edexcel Higher
-
Circle-Theorem-Proofs Edexcel Higher
-
Bearings-Scale-Drawing-Constructions-And-Loci Edexcel Higher5 主题
-
Angles-In-Polygons-And-Parallel-Lines Edexcel Higher3 主题
-
Symmetry-And-Shapes Edexcel Higher6 主题
-
Exchange-Rates-And-Best-Buys Edexcel Higher2 主题
-
Standard-And-Compound-Units Edexcel Higher5 主题
-
Direct-And-Inverse-Proportion Edexcel Higher2 主题
-
Problem-Solving-With-Ratios Edexcel Higher2 主题
-
Ratios Edexcel Higher3 主题
-
Sequences Edexcel Higher4 主题
-
Transformations-Of-Graphs Edexcel Higher2 主题
-
Graphing-Inequalities Edexcel Higher2 主题
-
Solving-Inequalities Edexcel Higher2 主题
-
Real-Life-Graphs Edexcel Higher4 主题
-
Estimating-Gradients-And-Areas-Under-Graphs Edexcel Higher2 主题
-
Equation-Of-A-Circle Edexcel Higher2 主题
-
Graphs-Of-Functions Edexcel Higher6 主题
-
Linear-Graphs Edexcel Higher4 主题
-
Coordinate-Geometry Edexcel Higher4 主题
-
Functions Edexcel Higher3 主题
-
Forming-And-Solving-Equations Edexcel Higher3 主题
-
Iteration Edexcel Higher1 主题
-
Simultaneous-Equations Edexcel Higher2 主题
-
Quadratic-Equations Edexcel Higher4 主题
-
Linear-Equations Edexcel Higher1 主题
-
Algebraic-Proof Edexcel Higher1 主题
-
Rearranging-Formulas Edexcel Higher2 主题
-
Algebraic-Fractions Edexcel Higher4 主题
-
Completing-The-Square Edexcel Higher1 主题
-
Factorising Edexcel Higher6 主题
-
Expanding-Brackets Edexcel Higher3 主题
-
Algebraic-Roots-And-Indices Edexcel Higher1 主题
-
Introduction Edexcel Higher7 主题
-
Using-A-Calculator Edexcel Higher1 主题
-
Surds Edexcel Higher2 主题
-
Rounding-Estimation-And-Bounds Edexcel Higher2 主题
-
Fractions-Decimals-And-Percentages Edexcel Higher3 主题
-
Simple-And-Compound-Interest-Growth-And-Decay Edexcel Higher4 主题
-
Percentages Edexcel Higher3 主题
-
Fractions Edexcel Higher4 主题
-
Powers-Roots-And-Standard-Form Edexcel Higher4 主题
-
Prime-Factors-Hcf-And-Lcm Edexcel Higher4 主题
-
Number-Operations Edexcel Higher10 主题
-
Product-Rule-For-Counting Edexcel Higher
-
Systematic-Lists Edexcel Higher
-
Related-Calculations Edexcel Higher
-
Multiplication-And-Division Edexcel Higher
-
Addition-And-Subtraction Edexcel Higher
-
Money-Calculations Edexcel Higher
-
Negative-Numbers Edexcel Higher
-
Irrational-Numbers Edexcel Higher
-
Order-Of-Operations-Bidmas-Bodmas Edexcel Higher
-
Mathematical-Symbols Edexcel Higher
-
Product-Rule-For-Counting Edexcel Higher
Rates-Of-Change-Of-Graphs Edexcel Higher
Exam code:1MA1
Rates of change of graphs
What is a rate-of-change graph?
-
A rate-of-change graph usually shows how a variable changes with time
-
The following are examples of rates-of-change graphs:
-
Speed against time
-
Speed is the rate of change of distance as time increases
-
-
Acceleration against time
-
Acceleration is the rate of change of velocity as time increases
-
-
The depth of water against time (e.g. in a container as it is filled with water)
-
Can rates-of-change graphs not be against time?
-
More generally, rate-of-change graphs can show any two different variables plotted against each other, not just time
-
E.g. the volume of air inside an inflating balloon plotted against the balloon’s radius
-
This shows the rate of change of volume as radius increases
-
-
E.g. the number of ice-creams sold plotted against the weather temperature
-
This shows the rate of change of number of ice-creams as temperature increases
-
-
How can I use gradients to find rates of change?
-
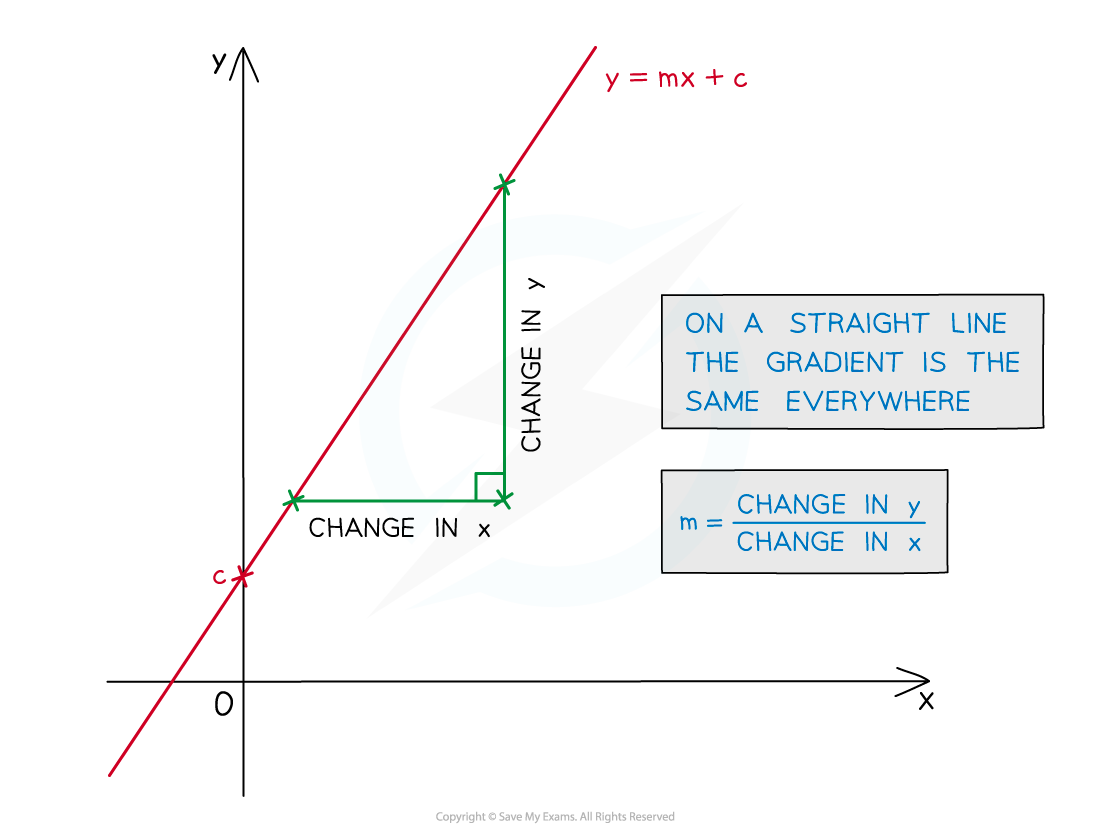
The gradient of the graph of y against x represents:
-
the amount of change in y for every 1 unit of increase in the x-direction
-
This is the amount of y per unit of x
-
-
This is called the rate of change of y against x
-
-
The units of gradients are the units of the y-axis, divided by the units of the x-axis
-
E.g. If the graph shows volume in cm3 on the y-axis and time in seconds on the x-axis, the rate of change is measured in cm3/s (or cm3s-1)
-
-
If the graph is a straight line the rate of change is constant
-
If the graph is horizontal, the rate of change is zero
-
y is not changing as x changes
-
-
How can I use tangents to find rates of change?
-
If the graph is a curve, you can draw a tangent at a point on the graph and find its gradient
-
This will be an estimate of the rate of change of y against x
-
-
The rate of change is greater when the graph is steeper
-
In the below image
-
tangents drawn at points A and B show the graph is steeper at B
-
therefore the rate of change at B is greater
-
-

-
On a distance-time graph, a tangent at a point on the curve can be used to estimate the velocity at that particular time
-
On a speed-time graph, a tangent at a point on the curve can be used to estimate the acceleration at that particular time
Examiner Tips and Tricks
-
The units of the gradient can help you understand what is happening in the context of an exam question
-
For example, if the y-axis is in dollars and the x-axis is in hours, the gradient represents the change in dollars per hour
-
Worked Example
(a) Each of the graphs below show the depth of water, d cm, in different containers that are being filled from a running tap of water.
Match each of the graphs 1, 2, 3, 4 with the containers A, B, C, D.
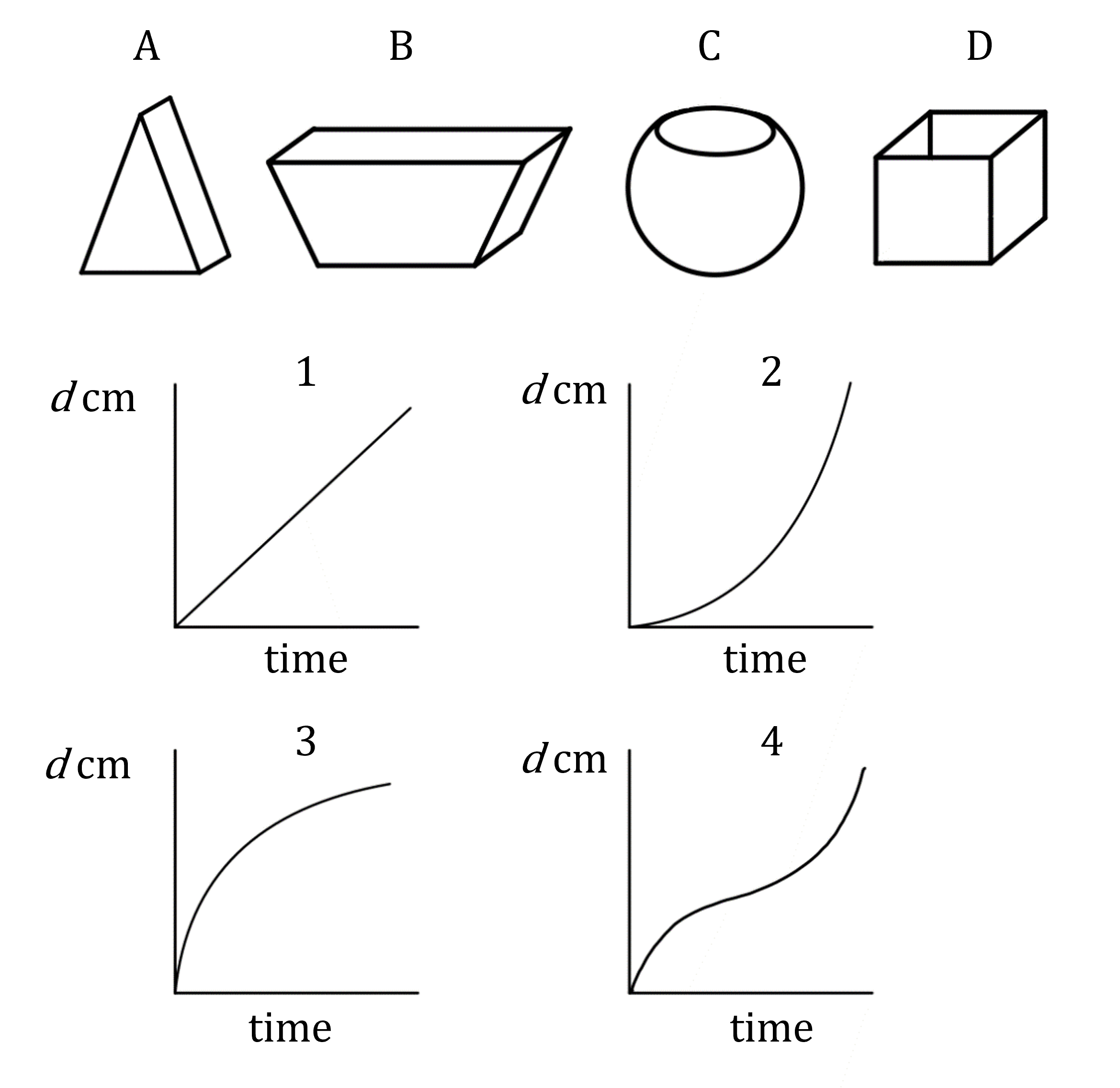
Considering graph 1: the gradient is constant
This means the rate of change is constant
So the depth increases at the same rate throughout
This matches container D which has vertical sides, so depth increases uniformly
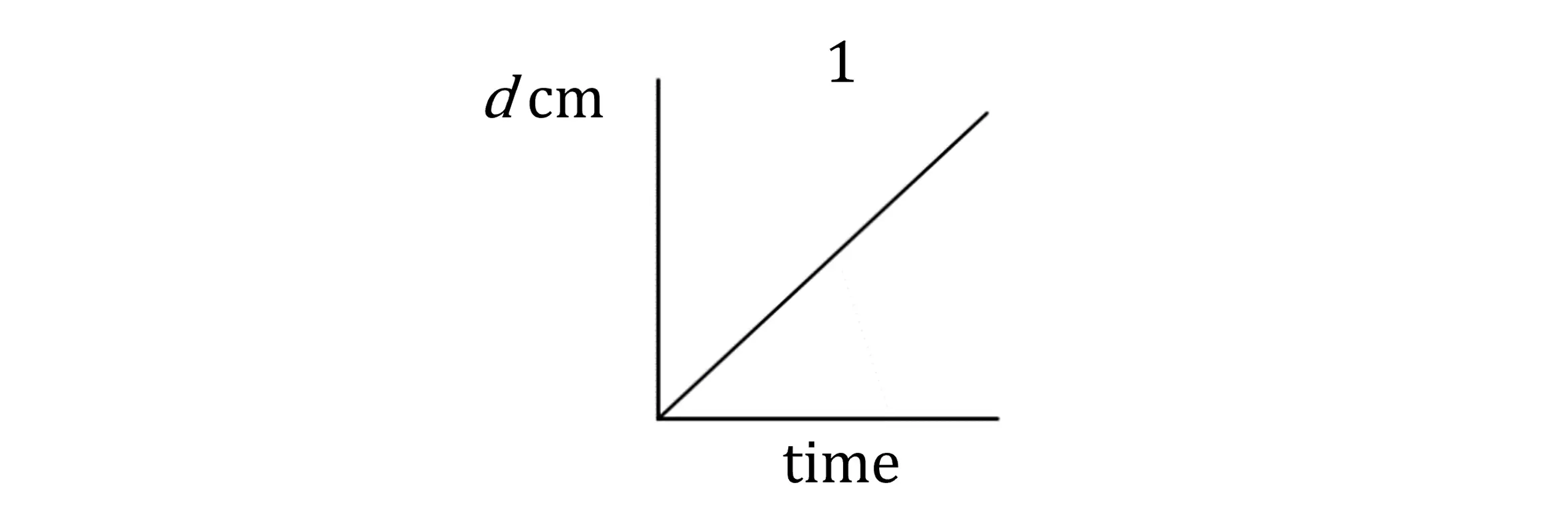
Graph 1 is container D
Considering graph 2: the gradient starts shallow and becomes steeper, meaning that the depth increases faster and faster at the end
This matches container A, which gets narrower towards the top, causing the depth to increase faster at the end
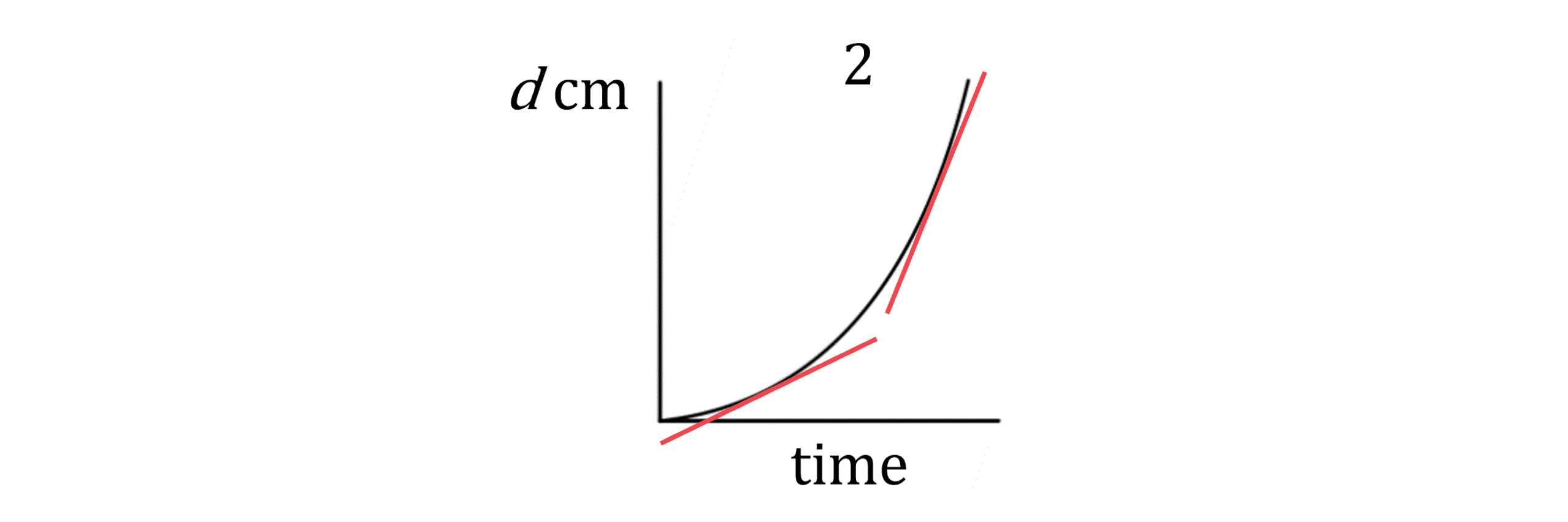
Graph 2 is container A
Considering graph 3: the gradient starts steep and becomes shallower, meaning that the depth increases at a slower and slower rate as time increases
This matches container B, which gets wider towards the top, causing the depth to increase more slowly at the end

Responses