Maths Gcse Edexcel Higher
-
Scatter-Graphs-And-Correlation Edexcel Higher2 主题
-
Cumulative-Frequency-And-Box-Plots Edexcel Higher4 主题
-
Histograms Edexcel Higher3 主题
-
Statistical-Diagrams Edexcel Higher7 主题
-
Averages-Ranges-And-Data Edexcel Higher8 主题
-
Capture-Recapture Edexcel Higher
-
Population-And-Sampling Edexcel Higher
-
Comparing-Data-Sets Edexcel Higher
-
Range-And-Interquartile-Range Edexcel Higher
-
Averages-From-Grouped-Data Edexcel Higher
-
Averages-From-Tables Edexcel Higher
-
Calculations-With-The-Mean Edexcel Higher
-
Mean-Median-And-Mode Edexcel Higher
-
Capture-Recapture Edexcel Higher
-
Combined-And-Conditional-Probability Edexcel Higher3 主题
-
Tree-Diagrams Edexcel Higher1 主题
-
Simple-Probability-Diagrams Edexcel Higher3 主题
-
Transformations Edexcel Higher5 主题
-
Vectors Edexcel Higher6 主题
-
3D-Pythagoras-And-Trigonometry Edexcel Higher1 主题
-
Sine-Cosine-Rule-And-Area-Of-Triangles Edexcel Higher4 主题
-
Pythagoras-And-Trigonometry Edexcel Higher4 主题
-
Area-And-Volume-Of-Similar-Shapes Edexcel Higher1 主题
-
Congruence-Similarity-And-Geometrical-Proof Edexcel Higher5 主题
-
Volume-And-Surface-Area Edexcel Higher3 主题
-
Circles-Arcs-And-Sectors Edexcel Higher2 主题
-
Area-And-Perimeter Edexcel Higher4 主题
-
Circle-Theorems Edexcel Higher7 主题
-
Circle-Theorem-Proofs Edexcel Higher
-
The-Alternate-Segment-Theorem Edexcel Higher
-
Angles-In-The-Same-Segment Edexcel Higher
-
Angles-In-Cyclic-Quadrilaterals Edexcel Higher
-
Theorems-With-Chords-And-Tangents Edexcel Higher
-
Angle-In-A-Semicircle Edexcel Higher
-
Angles-At-Centre-And-Circumference Edexcel Higher
-
Circle-Theorem-Proofs Edexcel Higher
-
Bearings-Scale-Drawing-Constructions-And-Loci Edexcel Higher5 主题
-
Angles-In-Polygons-And-Parallel-Lines Edexcel Higher3 主题
-
Symmetry-And-Shapes Edexcel Higher6 主题
-
Exchange-Rates-And-Best-Buys Edexcel Higher2 主题
-
Standard-And-Compound-Units Edexcel Higher5 主题
-
Direct-And-Inverse-Proportion Edexcel Higher2 主题
-
Problem-Solving-With-Ratios Edexcel Higher2 主题
-
Ratios Edexcel Higher3 主题
-
Sequences Edexcel Higher4 主题
-
Transformations-Of-Graphs Edexcel Higher2 主题
-
Graphing-Inequalities Edexcel Higher2 主题
-
Solving-Inequalities Edexcel Higher2 主题
-
Real-Life-Graphs Edexcel Higher4 主题
-
Estimating-Gradients-And-Areas-Under-Graphs Edexcel Higher2 主题
-
Equation-Of-A-Circle Edexcel Higher2 主题
-
Graphs-Of-Functions Edexcel Higher6 主题
-
Linear-Graphs Edexcel Higher4 主题
-
Coordinate-Geometry Edexcel Higher4 主题
-
Functions Edexcel Higher3 主题
-
Forming-And-Solving-Equations Edexcel Higher3 主题
-
Iteration Edexcel Higher1 主题
-
Simultaneous-Equations Edexcel Higher2 主题
-
Quadratic-Equations Edexcel Higher4 主题
-
Linear-Equations Edexcel Higher1 主题
-
Algebraic-Proof Edexcel Higher1 主题
-
Rearranging-Formulas Edexcel Higher2 主题
-
Algebraic-Fractions Edexcel Higher4 主题
-
Completing-The-Square Edexcel Higher1 主题
-
Factorising Edexcel Higher6 主题
-
Expanding-Brackets Edexcel Higher3 主题
-
Algebraic-Roots-And-Indices Edexcel Higher1 主题
-
Introduction Edexcel Higher7 主题
-
Using-A-Calculator Edexcel Higher1 主题
-
Surds Edexcel Higher2 主题
-
Rounding-Estimation-And-Bounds Edexcel Higher2 主题
-
Fractions-Decimals-And-Percentages Edexcel Higher3 主题
-
Simple-And-Compound-Interest-Growth-And-Decay Edexcel Higher4 主题
-
Percentages Edexcel Higher3 主题
-
Fractions Edexcel Higher4 主题
-
Powers-Roots-And-Standard-Form Edexcel Higher4 主题
-
Prime-Factors-Hcf-And-Lcm Edexcel Higher4 主题
-
Number-Operations Edexcel Higher10 主题
-
Product-Rule-For-Counting Edexcel Higher
-
Systematic-Lists Edexcel Higher
-
Related-Calculations Edexcel Higher
-
Multiplication-And-Division Edexcel Higher
-
Addition-And-Subtraction Edexcel Higher
-
Money-Calculations Edexcel Higher
-
Negative-Numbers Edexcel Higher
-
Irrational-Numbers Edexcel Higher
-
Order-Of-Operations-Bidmas-Bodmas Edexcel Higher
-
Mathematical-Symbols Edexcel Higher
-
Product-Rule-For-Counting Edexcel Higher
Hcf-And-Lcm Edexcel Higher
Exam code:1MA1
Highest common factor (HCF)
What is the highest common factor (HCF) of two numbers?
-
A common factor of two numbers is a value that both numbers can be divided by, leaving no remainder
-
1 is always a common factor of any two numbers
-
Any factor of a common factor will also be a common factor of the original two numbers
-
6 is a common factor of 24 and 30
-
Therefore 1, 2 and 3 are also common factors of 24 and 30
-
-
-
The highest common factor is the largest common factor of the two numbers
-
The highest common factor is useful when simplifying fractions or factorising expressions
-
How do I find the highest common factor (HCF) of two numbers?
-
To find common factors:
-
write out the factors of each number in a list
-
identify the numbers that appear in both lists
-
-
The highest common factor will be the largest factor that appears in both lists
How can I use a Venn diagram to find the highest common factor (HCF) of two numbers?
-
Write each number as a product of its prime factors
-
42 = 2×3×7 and 90 = 2×3×3×5
-
-
Find the prime factors that are common to both numbers and put these in the centre of the Venn diagram
-
42 and 90 both have a prime factor of 2
-
Put 2 in the centre of the diagram
-
-
Although 3 appears twice in the prime factors of 90, it appears once in the prime factors of 42
-
Put a single 3 in the centre of the diagram
-
-
If there are no common prime factors, put a 1 in the centre of the diagram
-
-
Put the remaining prime factors in the respective regions
-
7 would go in the region for 42
-
3 and 5 would go in the region for 90
-
-
The highest common factor is the product of the numbers in the centre
-
The HCF of 42 and 90 is 2×3, which is 6
-
-
If there are no common prime factors then the HCF is 1

How can I use the powers of prime factors to find the highest common factor (HCF) of two numbers?
-
Write each number as a product of the powers of its prime factors
-
24 = 23×3 and 60 = 22×3×5
-
-
Find all common prime factors and identify the highest power that appears in both numbers
-
The highest power of 2 in both is 22
-
22 is a common factor
-
-
The highest power of 3 in both is 31
-
3 is a common factor
-
-
No other prime number appears in both
-
-
The highest common factor is the product of the common powers of primes
-
The HCF of 24 and 60 is 22×3 which is 12
-
Examiner Tips and Tricks
-
The highest common factor of two numbers could be one of the numbers!
-
The highest common factor of 4 and 12 is 4
-
Worked Example
Find the highest common factor of 36 and 120.
Write both numbers as a product of prime factors
36 = 2×2×3×3 = 22 × 32
120 = 2×2×2×3×5 = 23 × 3 × 5
Write the prime factors in a Venn diagram
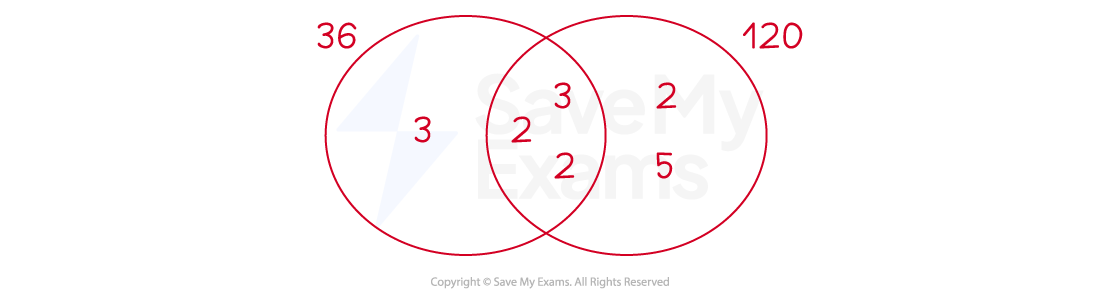
Multiply the common prime factors in the centre
HCF = 2 × 2 × 3
Alternatively, list the factors for each number
36: 1, 2, 3, 4, 6, 9, 12, 18, 36
120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Another alternative is to find the highest common powers of primes
22 and 31 are the highest common powers of primes
HCF = 22 × 31
HCF = 12
Lowest common multiple (LCM)
What is the lowest common multiple (LCM) of two numbers?
-
A common multiple of two numbers is a number that appears in both of their times tables
-
The product of the original two numbers is always a common multiple (but not necessarily the lowest)
-
Any multiple of a common multiple will also be a common multiple of the original two numbers
-
30 is a common multiple of 3 and 10
-
Therefore 60, 90, 120, … are also common multiples of 3 and 10
-
-
-
The lowest common multiple is the smallest common multiple between two numbers
-
This is useful when finding a common denominator and when adding or subtracting fractions
-
How do I find the lowest common multiple (LCM) of two numbers?
-
To find the lowest common multiple of two numbers:
-
write out the first few multiples of each number
-
identify the multiples that appear in both lists
-
If there are none then write out the next few multiples of each number until you find a common multiple
-
-
-
The lowest common multiple will be the smallest multiple that appears in both lists
How can I use a Venn diagram to find the lowest common multiple (LCM) of two numbers?
-
Write each number as a product of its prime factors
-
42 = 2×3×7 and 90 = 2×3×3×5
-
-
Find the prime factors that are common to both numbers and put these in the centre of the Venn diagram
-
42 and 90 both have a prime factor of 2
-
Put a 2 in the centre of the diagram
-
-
Although 3 appears twice in the prime factors of 90, it appears once in the prime factors of 42
-
Put a single 3 in the centre of the diagram
-
-
If there are no common prime factors then put a 1 in the centre of the diagram
-
-
Put the remaining prime factors in the respective regions
-
7 would go in the region for 42
-
3 and 5 would go in the region for 90
-
-
The lowest common multiple is the product of all the numbers in the Venn diagram
-
The LCM of 42 and 90 is 7×2×3×3×5, which is 630
-

How can I use the powers of prime factors to find the lowest common multiple (LCM) of two numbers?
-
Write each number as a product of the powers of its prime factors
-
<img alt=”72 equals 2 cubed cross times 3 squared” data-mathml=”<math ><semantics><mrow><mn>72</mn><mo>=</mo><msup><mn>2</mn><mn>3</mn></msup><mo>×</mo><msup><mn>3</mn><mn>2</mn></msup></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true,”toolbar”:”<toolbar ref=’general’><tab ref=’general’><removeItem ref=’setColor’/><removeItem ref=’bold’/><removeItem ref=’italic’/><removeItem ref=’autoItalic’/><removeItem ref=’setUnicode’/><removeItem ref=’mtext’ /><removeItem ref=’rtl’/><removeItem ref=’forceLigature’/><removeItem ref=’setFontFamily’ /><removeItem ref=’setFontSize’/></tab></toolbar>”}</annotation></semantics></math>” height=”23″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2223%22%20width%3D%2285%22%20wrs%3Abaseline%3D%2217%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmn%3E72%3C%2Fmn%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmsup%3E%3Cmn%3E2%3C%2Fmn%3E%3Cmn%3E3%3C%2Fmn%3E%3C%2Fmsup%3E%3Cmo%3E%26%23xD7%3B%3C%2Fmo%3E%3Cmsup%3E%3Cmn%3E3%3C%2Fmn%3E%3Cmn%3E2%3C%2Fmn%3E%3C%2Fmsup%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math102a87acd26f5771b4d57a7dfb3’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAABIWhlYWQQC2qxAAACuAAAADZoaGVhCGsXSAAAAvAAAAAkaG10eE2rRkcAAAMUAAAADGxvY2EAHTwYAAADIAAAABBtYXhwBT0FPgAAAzAAAAAgbmFtZaBxlY4AAANQAAABn3Bvc3QB9wD6AAAE8AAAACBwcmVwa1uragAABRAAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0A1%2F%2F%2FAAAAPQDX%2F%2F%2F%2FxP8rAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAIAgABVAtUCgAADAAcARhiwARQAsQAAExCxAAnksQABExCwBDyxBgj0sAI8MAGxCAETELEAA%2FawBzyxAQX1sAY8sgUHABD0sAI8sQkD5rEEBfWwAzwTMwEjETMBI4BVAgBVVf4AVQKA%2FdUCK%2F3VAAAAAAEAAAABAADVeM5BXw889QADBAD%2F%2F%2F%2F%2F1joTc%2F%2F%2F%2F%2F%2FWOhNzAAD%2FIASAA6sAAAAKAAIAAQAAAAAAAQAAA%2Bj%2FagAAF3AAAP%2B2BIAAAQAAAAAAAAAAAAAAAAAAAAMDUgBVA1YAgANWAIAAAAAAAAAAKAAAALIAAAEhAAEAAAADAF4ABQAAAAAAAgCABAAAAAAABAAA3gAAAAAAAAAVAQIAAAAAAAAAAQASAAAAAAAAAAAAAgAOABIAAAAAAAAAAwAwACAAAAAAAAAABAASAFAAAAAAAAAABQAWAGIAAAAAAAAABgAJAHgAAAAAAAAACAAcAIEAAQAAAAAAAQASAAAAAQAAAAAAAgAOABIAAQAAAAAAAwAwACAAAQAAAAAABAASAFAAAQAAAAAABQAWAGIAAQAAAAAABgAJAHgAAQAAAAAACAAcAIEAAwABBAkAAQASAAAAAwABBAkAAgAOABIAAwABBAkAAwAwACAAAwABBAkABAASAFAAAwABBAkABQAWAGIAAwABBAkABgAJAHgAAwABBAkACAAcAIEATQBhAHQAaAAgAEYAbwBuAHQAUgBlAGcAdQBsAGEAcgBNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAIABNAGEAdABoACAARgBvAG4AdABNAGEAdABoACAARgBvAG4AdABWAGUAcgBzAGkAbwBuACAAMQAuADBNYXRoX0ZvbnQATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAADAAAAAAAAAfQA%2BgAAAAAAAAAAAAAAAAAAAAAAAAAAuQcRAACNhRgAsgAAABUUE7EAAT8%3D)format(‘truetype’)%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2217%22%3E72%3C%2Ftext%3E%3Ctext%20font-family%3D%22math102a87acd26f5771b4d57a7dfb3%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2226.5%22%20y%3D%2217%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2239.5%22%20y%3D%2217%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2213%22%20text-anchor%3D%22middle%22%20x%3D%2247.5%22%20y%3D%2212%22%3E3%3C%2Ftext%3E%3Ctext%20font-family%3D%22math102a87acd26f5771b4d57a7dfb3%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2259.5%22%20y%3D%2217%22%3E%26%23xD7%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Rom
-

Responses