Maths Gcse Edexcel Foundation
-
Scatter-Graphs-And-Correlation Edexcel Foundation2 主题
-
Statistical-Diagrams Edexcel Foundation8 主题
-
Comparing-Statistical-Diagrams Edexcel Foundation
-
Reading-And-Interpreting-Statistical-Diagrams Edexcel Foundation
-
Time-Series-Graphs Edexcel Foundation
-
Pie-Charts Edexcel Foundation
-
Frequency-Polygons Edexcel Foundation
-
Bar-Charts-And-Pictograms Edexcel Foundation
-
Tally-Charts-And-Frequency-Tables Edexcel Foundation
-
Stem-And-Leaf-Diagrams Edexcel Foundation
-
Comparing-Statistical-Diagrams Edexcel Foundation
-
Statistics-Toolkit Edexcel Foundation7 主题
-
Tree-Diagrams-And-Combined-Probability Edexcel Foundation2 主题
-
Simple-Probability-Diagrams Edexcel Foundation4 主题
-
Probability-Toolkit Edexcel Foundation3 主题
-
Transformations Edexcel Foundation4 主题
-
Vectors Edexcel Foundation3 主题
-
Volume-And-Surface-Area Edexcel Foundation3 主题
-
Circles-Arcs-And-Sectors Edexcel Foundation3 主题
-
Area-And-Perimeter Edexcel Foundation4 主题
-
Pythagoras-And-Trigonometry Edexcel Foundation5 主题
-
Congruence-Similarity-And-Geometrical-Proof Edexcel Foundation5 主题
-
Bearings-Scale-Drawing-Constructions-And-Loci Edexcel Foundation5 主题
-
2D-And-3D-Shapes Edexcel Foundation4 主题
-
Angles-In-Polygons-And-Parallel-Lines Edexcel Foundation5 主题
-
Geometry-Toolkit Edexcel Foundation4 主题
-
Exchange-Rates-And-Best-Buys Edexcel Foundation2 主题
-
Standard-And-Compound-Units Edexcel Foundation5 主题
-
Direct-And-Inverse-Proportion Edexcel Foundation1 主题
-
Ratio-Problem-Solving Edexcel Foundation2 主题
-
Ratio-Toolkit Edexcel Foundation3 主题
-
Sequences Edexcel Foundation4 主题
-
Solving-Inequalities Edexcel Foundation3 主题
-
Real-Life-Graphs Edexcel Foundation4 主题
-
Graphs-Of-Functions Edexcel Foundation3 主题
-
Linear-Graphs Edexcel Foundation3 主题
-
Coordinate-Geometry Edexcel Foundation3 主题
-
Functions Edexcel Foundation1 主题
-
Forming-And-Solving-Equations Edexcel Foundation2 主题
-
Simultaneous-Equations Edexcel Foundation1 主题
-
Solving-Quadratic-Equations Edexcel Foundation1 主题
-
Linear-Equations Edexcel Foundation3 主题
-
Algebraic-Reasoning Edexcel Foundation1 主题
-
Rearranging-Formulas Edexcel Foundation1 主题
-
Factorising Edexcel Foundation3 主题
-
Expanding-Brackets Edexcel Foundation2 主题
-
Algebraic-Roots-And-Indices Edexcel Foundation1 主题
-
Algebra-Toolkit Edexcel Foundation4 主题
-
Using-A-Calculator Edexcel Foundation1 主题
-
Exact-Values Edexcel Foundation1 主题
-
Rounding-Estimation-And-Error-Intervals Edexcel Foundation4 主题
-
Fractions-Decimals-And-Percentages Edexcel Foundation2 主题
-
Simple-And-Compound-Interest-Growth-And-Decay Edexcel Foundation4 主题
-
Percentages Edexcel Foundation5 主题
-
Fractions Edexcel Foundation6 主题
-
Multiplying-And-Dividing-Fractions Edexcel Foundation
-
Adding-And-Subtracting-Fractions Edexcel Foundation
-
Mixed-Numbers-And-Improper-Fractions Edexcel Foundation
-
Equivalent-And-Simplified-Fractions Edexcel Foundation
-
Fractions-Of-Amounts Edexcel Foundation
-
Introduction-To-Fractions Edexcel Foundation
-
Multiplying-And-Dividing-Fractions Edexcel Foundation
-
Powers-Roots-And-Standard-Form Edexcel Foundation4 主题
-
Types-Of-Number-Prime-Factors-Hcf-And-Lcm Edexcel Foundation6 主题
-
Number-Toolkit Edexcel Foundation9 主题
-
Counting-Principles Edexcel Foundation
-
Related-Calculations Edexcel Foundation
-
Multiplication-And-Division Edexcel Foundation
-
Addition-And-Subtraction Edexcel Foundation
-
Money-Calculations Edexcel Foundation
-
Negative-Numbers Edexcel Foundation
-
Place-Value Edexcel Foundation
-
Order-Of-Operations-Bidmas-Bodmas Edexcel Foundation
-
Mathematical-Operations Edexcel Foundation
-
Counting-Principles Edexcel Foundation
Frequency-Polygons Edexcel Foundation
Exam code:1MA1
Frequency polygons
What are the key features of a frequency polygon?
-
Frequency polygons are a very simple way of showing frequencies for continuous, grouped data and give a quick guide to how frequencies change from one class to the next
-
Apart from plotting and joining up points with straight lines there are 2 rules for frequency polygons:
-
Plot points at the MIDPOINT of class intervals
-
Unless one of the frequencies is 0 do not join the frequency polygon to the x-axis, and do not join the first point to the last one
-
-
The result is not actually a polygon but more of an open one that ‘floats’ in mid-air!
-
You may be asked to draw a frequency polygon and/or use it to make comments and compare data
How do I draw a frequency polygon?
-
This is easiest shown by an example
-
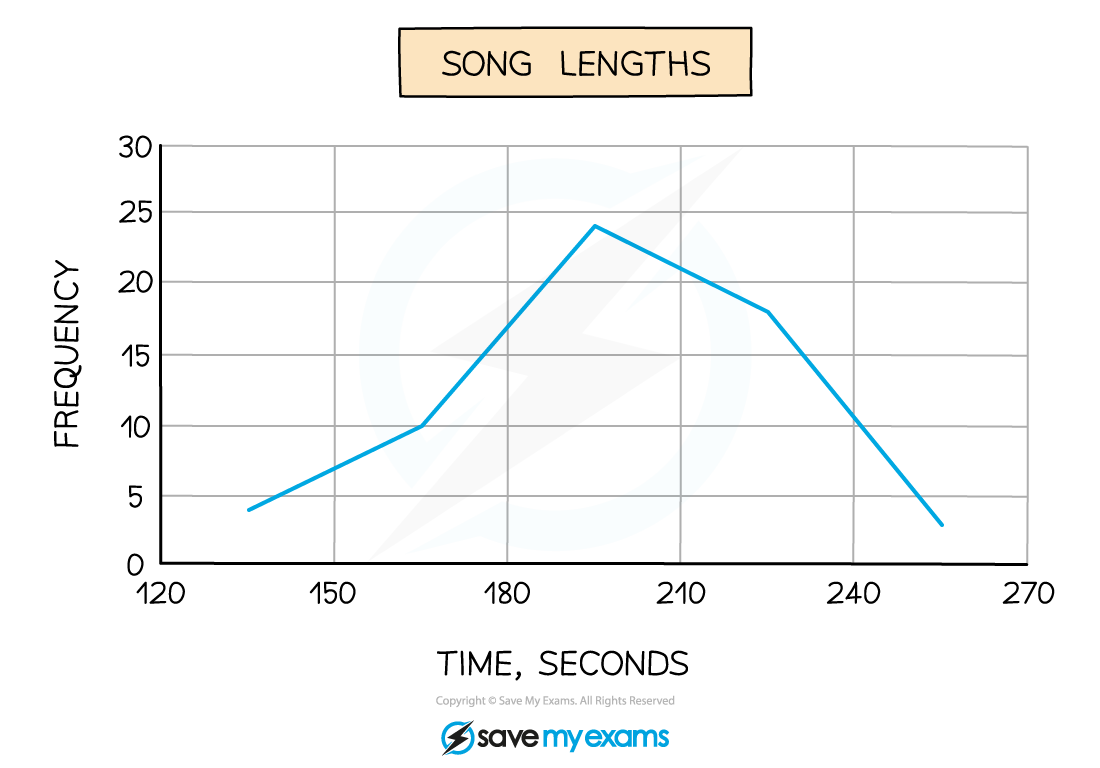
e.g. The lengths of 59 songs, in seconds, are recorded in the table below
-
|
Song length |
Frequency |
|
120 ≤ t < 150 |
4 |
|
150 ≤ t < 180 |
10 |
|
180 ≤ t < 210 |
24 |
|
210 ≤ t < 240 |
18 |
|
240 ≤ t < 270 |
3 |
-
Frequencies are plotted at the midpoints of the class intervals
-
so in this case we would plot the points (135, 4), (165, 10), (195, 24), (225, 18) and (255, 3)
-
Join these up with straight lines (but do not join the last to the first!)
-
How do I use and interpret a frequency polygon?
-
Think about what you could you say about the data above, particularly by looking at the diagram only?
-
The two things to look for are averages and spread
-
The modal class is 180 ≤ t < 210
-
It would be acceptable to say that 195 seconds is (an estimate of) the modal song length
-
The diagram (rather than the table) shows (an estimate of) the range of song lengths is 255 – 135 = 120 seconds
-
If 2 frequency polygons are drawn on the same graph comparisons between the 2 sets of data can be made
-
-
Examiner Tips and Tricks
-
Jot down the midpoints next to the frequencies so you are not trying to work them out in your head while also concentrating on actually plotting the points
Worked Example
A local council ran a campaign to encourage households to waste less food.
To compare the impact of the campaign the council recorded the weight of food waste produced by 30 households in a week both before and after the campaign.
The results are shown in the table below.
|
Food waste |
Frequency |
Frequency |
|
1 ≤ w < 1.4 |
3 |
5 |
|
1.4 ≤ w < 1.8 |
4 |
8 |
|
1.8 ≤ w < 2.2 |
8 |
14 |
|
2.2 ≤ w < 2.6 |
10 |
3 |
|
2.6 ≤ w < 3 |
5 |
1 |
a)
On the same diagram, draw two frequency polygons, one for before the council’s campaign and one for after.
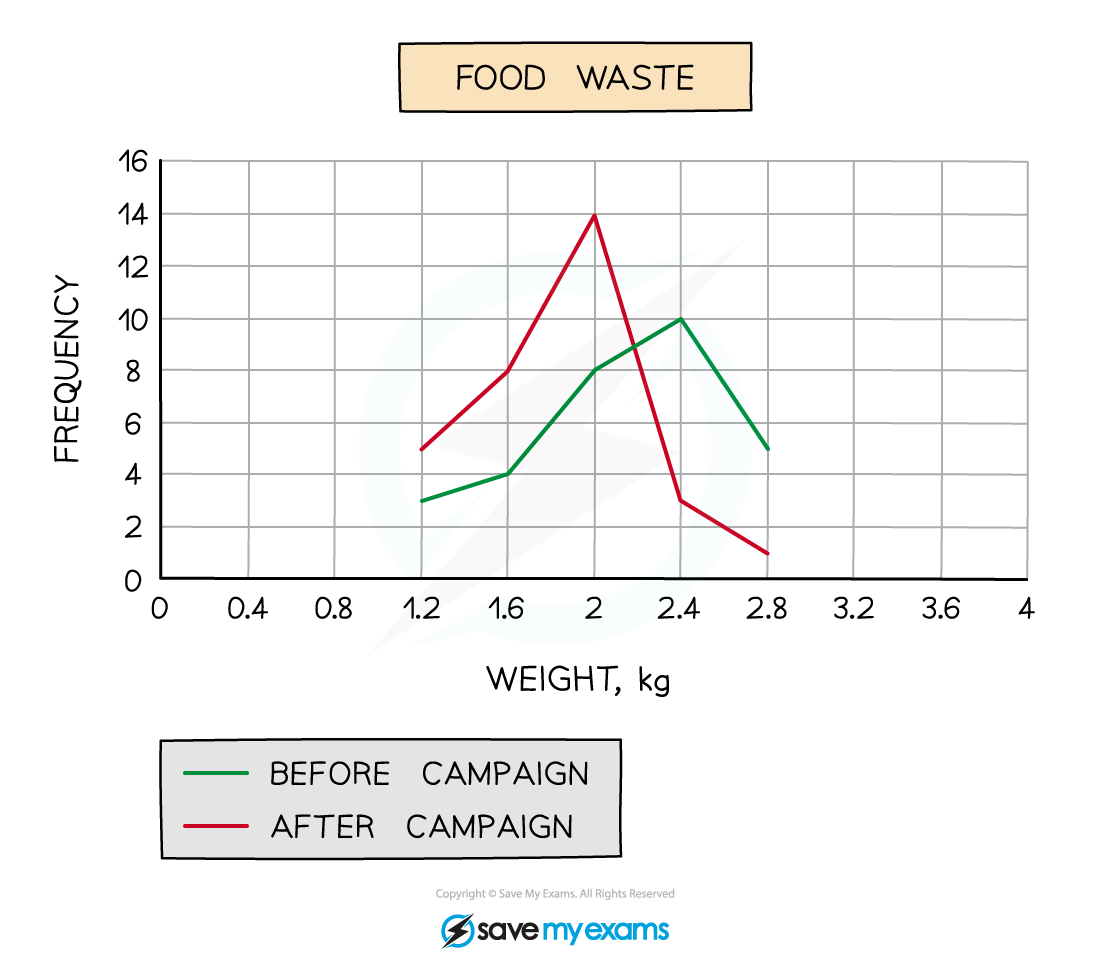
Remember to include a key to show which frequency polygon is which.
b)
Comment on whether you think the council’s campaign has been successful or not and give a reason why.
The council campaign has been successful as the modal amount of waste has reduced from 2.4 kg of food waste per week to 2 kg
Remember to look for average(s) and/or spread – the mode (average) is appropriate in this case.

Responses