Maths Gcse Edexcel Foundation
-
Scatter-Graphs-And-Correlation Edexcel Foundation2 主题
-
Statistical-Diagrams Edexcel Foundation8 主题
-
Comparing-Statistical-Diagrams Edexcel Foundation
-
Reading-And-Interpreting-Statistical-Diagrams Edexcel Foundation
-
Time-Series-Graphs Edexcel Foundation
-
Pie-Charts Edexcel Foundation
-
Frequency-Polygons Edexcel Foundation
-
Bar-Charts-And-Pictograms Edexcel Foundation
-
Tally-Charts-And-Frequency-Tables Edexcel Foundation
-
Stem-And-Leaf-Diagrams Edexcel Foundation
-
Comparing-Statistical-Diagrams Edexcel Foundation
-
Statistics-Toolkit Edexcel Foundation7 主题
-
Tree-Diagrams-And-Combined-Probability Edexcel Foundation2 主题
-
Simple-Probability-Diagrams Edexcel Foundation4 主题
-
Probability-Toolkit Edexcel Foundation3 主题
-
Transformations Edexcel Foundation4 主题
-
Vectors Edexcel Foundation3 主题
-
Volume-And-Surface-Area Edexcel Foundation3 主题
-
Circles-Arcs-And-Sectors Edexcel Foundation3 主题
-
Area-And-Perimeter Edexcel Foundation4 主题
-
Pythagoras-And-Trigonometry Edexcel Foundation5 主题
-
Congruence-Similarity-And-Geometrical-Proof Edexcel Foundation5 主题
-
Bearings-Scale-Drawing-Constructions-And-Loci Edexcel Foundation5 主题
-
2D-And-3D-Shapes Edexcel Foundation4 主题
-
Angles-In-Polygons-And-Parallel-Lines Edexcel Foundation5 主题
-
Geometry-Toolkit Edexcel Foundation4 主题
-
Exchange-Rates-And-Best-Buys Edexcel Foundation2 主题
-
Standard-And-Compound-Units Edexcel Foundation5 主题
-
Direct-And-Inverse-Proportion Edexcel Foundation1 主题
-
Ratio-Problem-Solving Edexcel Foundation2 主题
-
Ratio-Toolkit Edexcel Foundation3 主题
-
Sequences Edexcel Foundation4 主题
-
Solving-Inequalities Edexcel Foundation3 主题
-
Real-Life-Graphs Edexcel Foundation4 主题
-
Graphs-Of-Functions Edexcel Foundation3 主题
-
Linear-Graphs Edexcel Foundation3 主题
-
Coordinate-Geometry Edexcel Foundation3 主题
-
Functions Edexcel Foundation1 主题
-
Forming-And-Solving-Equations Edexcel Foundation2 主题
-
Simultaneous-Equations Edexcel Foundation1 主题
-
Solving-Quadratic-Equations Edexcel Foundation1 主题
-
Linear-Equations Edexcel Foundation3 主题
-
Algebraic-Reasoning Edexcel Foundation1 主题
-
Rearranging-Formulas Edexcel Foundation1 主题
-
Factorising Edexcel Foundation3 主题
-
Expanding-Brackets Edexcel Foundation2 主题
-
Algebraic-Roots-And-Indices Edexcel Foundation1 主题
-
Algebra-Toolkit Edexcel Foundation4 主题
-
Using-A-Calculator Edexcel Foundation1 主题
-
Exact-Values Edexcel Foundation1 主题
-
Rounding-Estimation-And-Error-Intervals Edexcel Foundation4 主题
-
Fractions-Decimals-And-Percentages Edexcel Foundation2 主题
-
Simple-And-Compound-Interest-Growth-And-Decay Edexcel Foundation4 主题
-
Percentages Edexcel Foundation5 主题
-
Fractions Edexcel Foundation6 主题
-
Multiplying-And-Dividing-Fractions Edexcel Foundation
-
Adding-And-Subtracting-Fractions Edexcel Foundation
-
Mixed-Numbers-And-Improper-Fractions Edexcel Foundation
-
Equivalent-And-Simplified-Fractions Edexcel Foundation
-
Fractions-Of-Amounts Edexcel Foundation
-
Introduction-To-Fractions Edexcel Foundation
-
Multiplying-And-Dividing-Fractions Edexcel Foundation
-
Powers-Roots-And-Standard-Form Edexcel Foundation4 主题
-
Types-Of-Number-Prime-Factors-Hcf-And-Lcm Edexcel Foundation6 主题
-
Number-Toolkit Edexcel Foundation9 主题
-
Counting-Principles Edexcel Foundation
-
Related-Calculations Edexcel Foundation
-
Multiplication-And-Division Edexcel Foundation
-
Addition-And-Subtraction Edexcel Foundation
-
Money-Calculations Edexcel Foundation
-
Negative-Numbers Edexcel Foundation
-
Place-Value Edexcel Foundation
-
Order-Of-Operations-Bidmas-Bodmas Edexcel Foundation
-
Mathematical-Operations Edexcel Foundation
-
Counting-Principles Edexcel Foundation
Angles-Of-Elevation-And-Depression- Edexcel Foundation
Exam code:1MA1
Elevation & depression
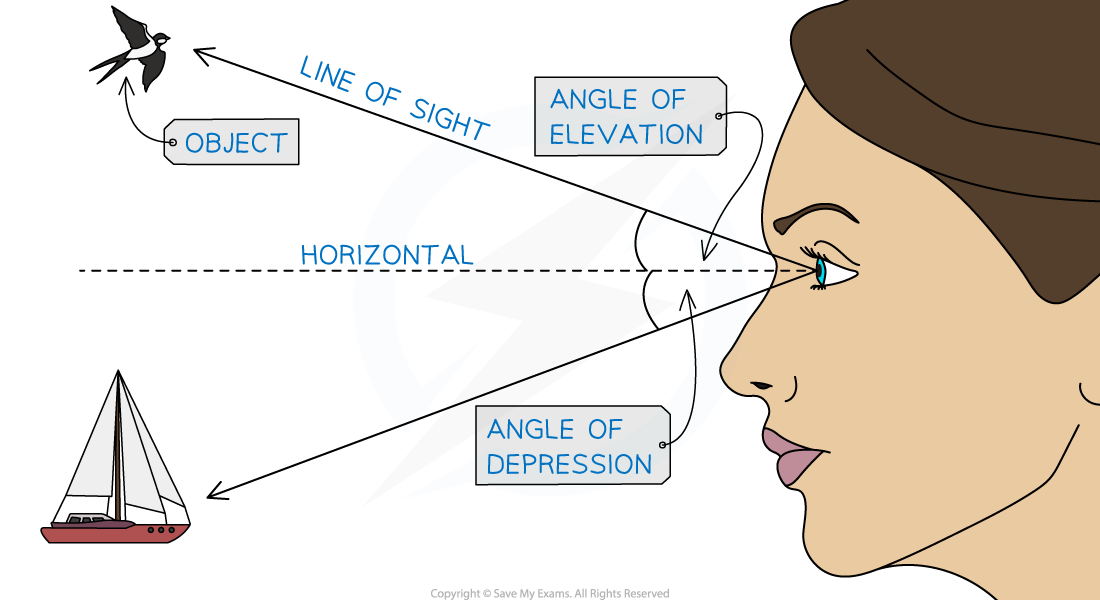
What are angles of elevation and depression?
-
An angle of elevation or depression is the angle measured between the horizontal and the line of sight
-
Looking up at an object creates an angle of elevation
-
Looking down at an object creates an angle of depression
-
-
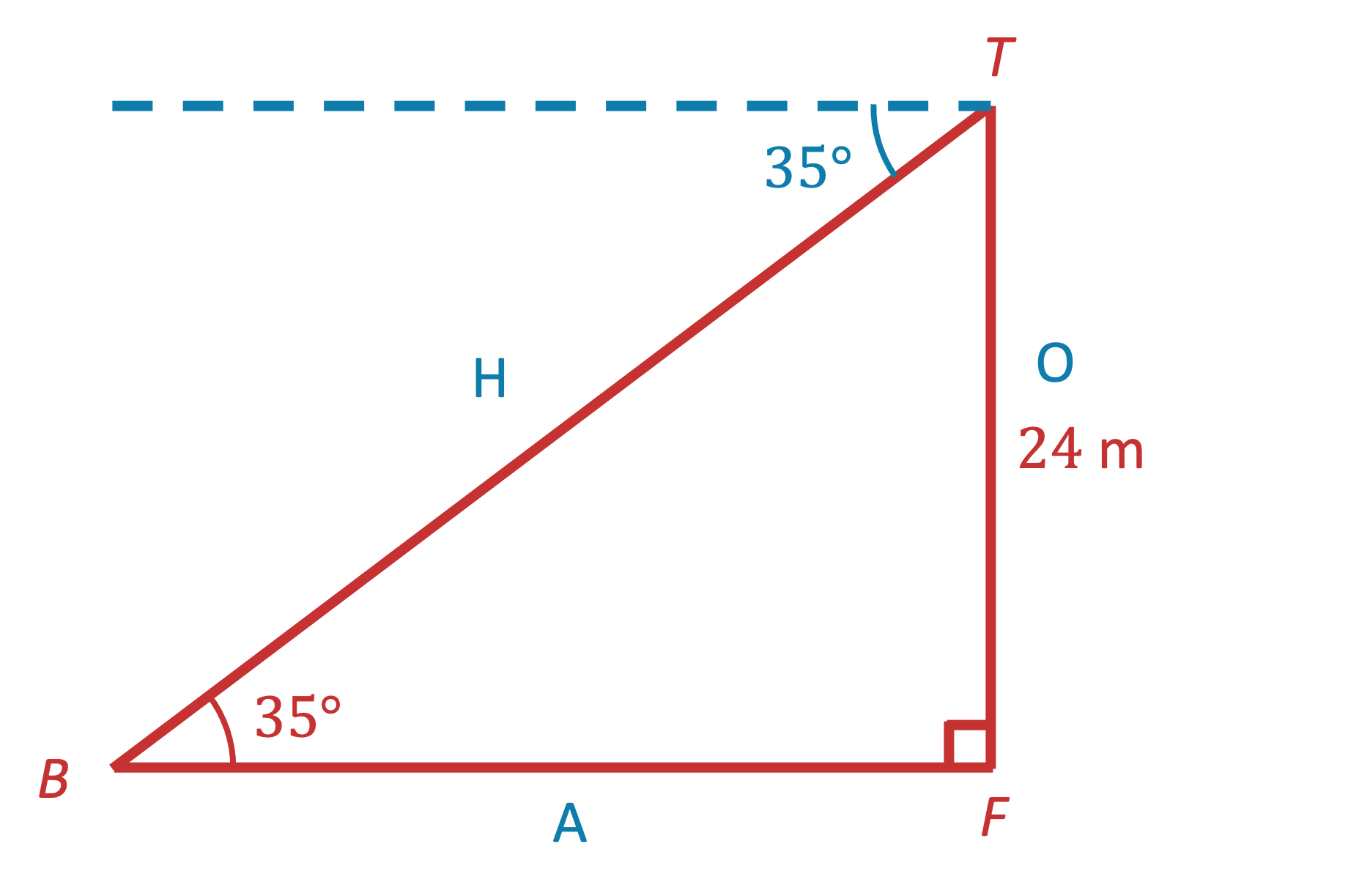
Right-angled trigonometry can be used to find
-
an angle of elevation or depression
-
or a missing distance
-
-
The tan ratio is often used in real-life scenarios
-
You may know the height of an object and want to find the distance you are from it
-
You may know the distance you are from an object and want to find its height
-
Examiner Tips and Tricks
It may be useful to draw more than one diagram if the triangles that you are interested in overlap one another.
Worked Example
A cliff is perpendicular to the sea and the top of the cliff, T, stands 24 metres above the level of the sea.
The angle of depression from the top of the cliff to a boat at sea is 35°.
At a point metres vertically up from the foot the cliff is a flag marker, M.
The angle of elevation from the boat, B, to the flag marker is 18°.
(a) Draw a diagram of the situation. Label all the angles and distances given above.
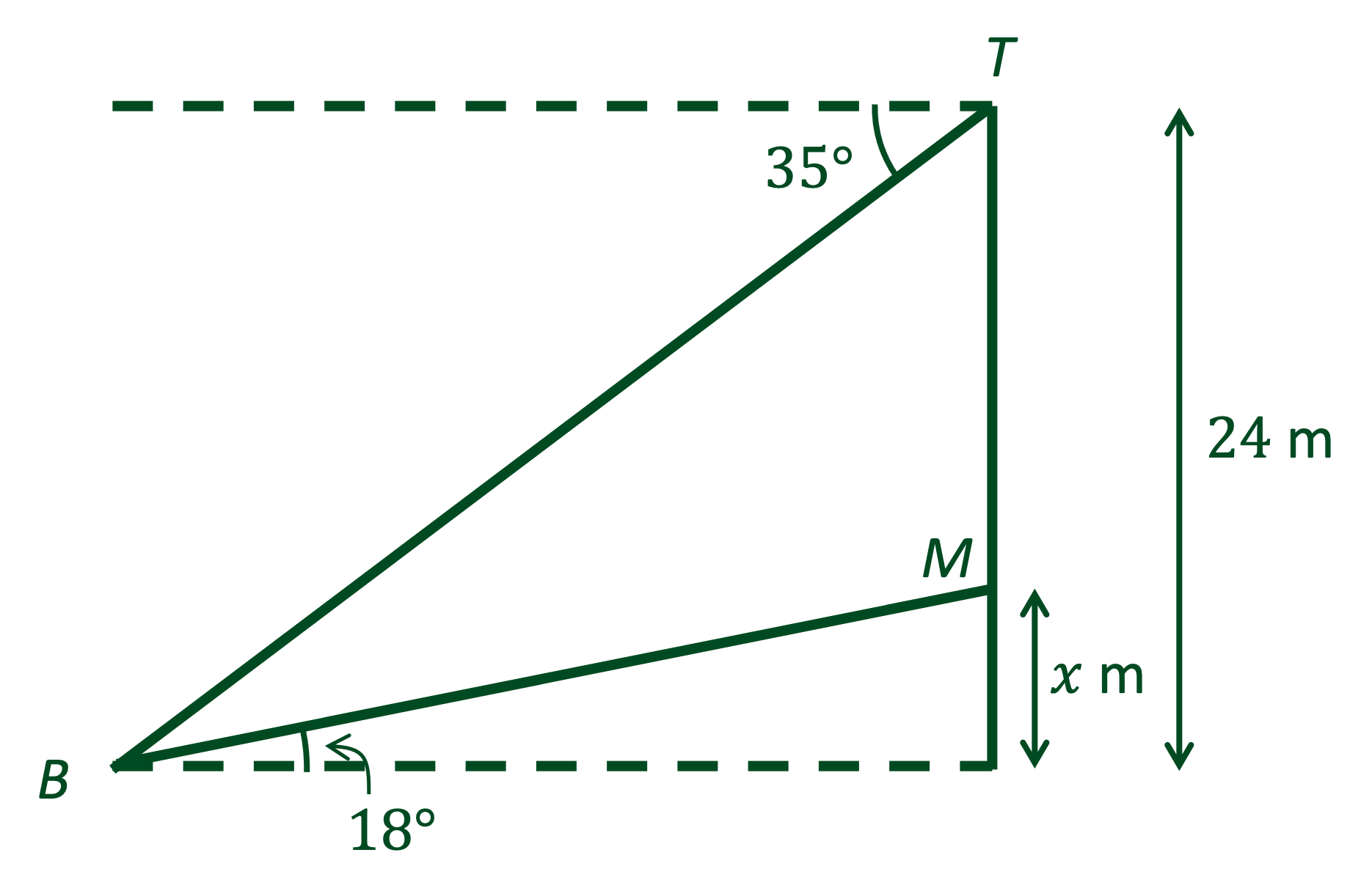
(b) Find the distance from the boat to the foot of the cliff.
Consider triangle TBF where F is the foot of the cliff
Angle TBF = 35º because of alternate angles
Use SOHCAHTOA to find the missing distance
We know the opposite (TF) and we want to find the adjacent (BF), so use
<img alt=”table row cell tan space 35 end cell equals cell fraction numerator 24 over denominator B F end fraction end cell row cell B F end cell equals cell fraction numerator 24 over denominator tan space 35 end fraction end cell row cell B F end cell equals cell 34.27555… end cell end table” data-mathml=”<math ><semantics><mtable columnspacing=”0px” columnalign=”right center left”><mtr><mtd><mi>tan</mi><mo> </mo><mn>35</mn></mtd><mtd><mo>=</mo></mtd><mtd><mfrac><mn>24</mn><mrow><mi>B</mi><mi>F</mi></mrow></mfrac></mtd></mtr><mtr><mtd><mi>B</mi><mi>F</mi></mtd><mtd><mo>=</mo></mtd><mtd><mfrac><mn>24</mn><mrow><mi>tan</mi><mo> </mo><mn>35</mn></mrow></mfrac></mtd></mtr><mtr><mtd><mi>B</mi><mi>F</mi></mtd><mtd><mo>=</mo></mtd><mtd><mn>34</mn><mo>.</mo><mn>27555</mn><mo>.</mo><mo>.</mo><mo>.</mo></mtd></mtr></mtable><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true,”toolbar”:”<toolbar ref=’general’><tab ref=’general’><removeItem ref=’setColor’/><removeItem ref=’bold’/><removeItem ref=’italic’/><removeItem ref=’autoItalic’/><removeItem ref=’setUnicode’/><removeItem ref=’mtext’ /><removeItem ref=’rtl’/><removeItem ref=’forceLigature’/><removeItem ref=’setFontFamily’ /><removeItem ref=’setFontSize’/></tab></toolbar>”}</annotation></semantics></math>” data-type=”working” height=”124″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%22124%22%20width%3D%22145%22%20wrs%3Abaseline%3D%2261%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmtable%20columnalign%3D%22right%20center%20left%22%20columnspacing%3D%220px%22%3E%3Cmtr%3E%3Cmtd%3E%3Cmi%3Etan%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmn%3E35%3C%2Fmn%3E%3C%2Fmtd%3E%3Cmtd%3E%3Cmo%3E%3D%3C%2Fmo%3E%3C%2Fmtd%3E%3Cmtd%3E%3Cmfrac%3E%3Cmn%3E24%3C%2Fmn%3E%3Cmrow%3E%3Cmi%3EB%3C%2Fmi%3E%3Cmi%3EF%3C%2Fmi%3E%3C%2Fmrow%3E%3C%2Fmfrac%3E%3C%2Fmtd%3E%3C%2Fmtr%3E%3Cmtr%3E%3Cmtd%3E%3Cmi%3EB%3C%2Fmi%3E%3Cmi%3EF%3C%2Fmi%3E%3C%2Fmtd%3E%3Cmtd%3E%3Cmo%3E%3D%3C%2Fmo%3E%3C%2Fmtd%3E%3Cmtd%3E%3Cmfrac%3E%3Cmn%3E24%3C%2Fmn%3E%3Cmrow%3E%3Cmi%3Etan%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmn%3E35%3C%2Fmn%3E%3C%2Fmrow%3E%3C%2Fmfrac%3E%3C%2Fmtd%3E%3C%2Fmtr%3E%3Cmtr%3E%3Cmtd%3E%3Cmi%3EB%3C%2Fmi%3E%3Cmi%3EF%3C%2Fmi%3E%3C%2Fmtd%3E%3Cmtd%3E%3Cmo%3E%3D%3C%2Fmo%3E%3C%2Fmtd%3E%3Cmtd%3E%3Cmn%3E34%3C%2Fmn%3E%3Cmo%3E.%3C%2Fmo%3E%3Cmn%3E27555%3C%2Fmn%3E%3Cmo%3E.%3C%2Fmo%3E%3Cmo%3E.%3C%2Fmo%3E%3Cmo%3E.%3C%2Fmo%3E%3C%2Fmtd%3E%3C%2Fmtr%3E%3C%2Fmtable%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math11824c643d1feb4da18b28ed527’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAAA%2BGhlYWQQC2qxAAACjAAAADZoaGVhCGsXSAAAAsQAAAAkaG10eE2rRkcAAALoAAAADGxvY2EAHTwYAAAC9AAAABBtYXhwBT0FPgAAAwQAAAAgbmFtZaBxlY4AAAMkAAABn3Bvc3QB9wD6AAAExAAAACBwcmVwa1uragAABOQAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAC4APf%2F%2FAAAALgA9%2F%2F%2F%2F0%2F%2FFAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAEAIAAAAKAAgAADAC8YAbAEELAD1LADELAC1LADELAAPLACELABPACwBBCwA9SwAxCwAjywABCwATwwMTczFSMggICAgAACAIAA6wLVAhUAAwAHAGUYAbAIELAG1LAGELAF1LAIELAB1LABELAA1LAGELAHPLAFELAEPLABELACPLAAELADPACwCBCwBtSwBhCwB9SwBxCwAdSwARCwAtSwBhCwBTywBxCwBDywARCwADywAhCwAzwxMBMhNSEdASE1gAJV%2FasCVQHAVdVVVQABAAAAAQAA1XjOQV8PPPUAAwQA%2F%2F%2F%2F%2F9Y6E3P%2F%2F%2F%2F%2F1joTcwAA%2FyAEgAOrAAAACgACAAEAAAAAAAEAAAPo%2F2oAABdwAAD%2FtgSAAAEAAAAAAAAAAAAAAAAAAAADA1IAVQDIACADVgCAAAAAAAAAACgAAABuAAAA%2BAABAAAAAwBeAAUAAAAAAAIAgAQAAAAAAAQAAN4AAAAAAAAAFQECAAAAAAAAAAEAEgAAAAAAAAAAAAIADgASAAAAAAAAAAMAMAAgAAAAAAAAAAQAEgBQAAAAAAAAAAUAFgBiAAAAAAAAAAYACQB4AAAAAAAAAAgAHACBAAEAAAAAAAEAEgAAAAEAAAAAAAIADgASAAEAAAAAAAMAMAAgAAEAAAAAAAQAEgBQAAEAAAAAAAUAFgBiAAEAAAAAAAYACQB4AAEAAAAAAAgAHACBAAMAAQQJAAEAEgAAAAMAAQQJAAIADgASAAMAAQQJAAMAMAAgAAMAAQQJAAQAEgBQAAMAAQQJAAUAFgBiAAMAAQQJAAYACQB4AAMAAQQJAAgAHACBAE0AYQB0AGgAIABGAG8AbgB0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAATQBhAHQAaAAgAEYAbwBuAHQATQBhAHQAaAAgAEYAbwBuAHQAVgBlAHIAcwBpAG8AbgAgADEALgAwTWF0aF9Gb250AE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAAAwAAAAAAAAH0APoAAAAAAAAAAAAAAAAAAAAAAAAAALkHEQAAjYUYALIAAAAVFBOxAAE%2F)format(‘truetype’)%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2211.5%22%20y%3D%2230%22%3Etan%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2235.5%22%20y%3D%2230%22%3E35%3C%2Ftext%3E%3Ctext%20font-family%3D%22math11824c643d1feb4da18b28ed527%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2252.5%22%20y%3D%2230%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20×1%3D%2263.5%22%20×2%3D%2289.5%22%20y1%3D%2223.5%22%20y2%3D%2223.5%22%2F%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2277.5%22%20y%3D%2216%22%3E24%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%2

Responses