Equations-Of-Straight-Lines-Y-Equals-Mx-And-C Edexcel Foundation

课 Progress

0% Complete

Exam code:1MA1

Finding equations of straight lines

What is the equation of a straight line?

The general equation of a straight line is y = mx + c where
- m is the gradient
- c is the y-intercept
  - The value where it cuts the y-axis
y = 5x + 2 is a straight line with
- gradient 5
- y-intercept 2
y = 3 – 4x is a straight line with
- gradient -4
- y-intercept 3

How do I find the equation of a straight line from a graph?

Find the gradient by drawing a triangle and using
- $gradient equals rise over run$
  - Positive for uphill lines, negative for downhill
Read off the y-intercept from the graph
- Where it cuts the y-axis
Substitute these values into y = mx + c

What if no y-intercept is shown?

If you can’t read off the y-intercept
- find any point on the line
- substitute it into the equation
- solve to find c
For example, a line with gradient 6 passes through (2, 15)
- The y-intercept is unknown
  - Write y = 6x + c
- Substitute in x = 2 and y = 15
  - 15 = 6 × 2 + c
  - 15 = 12 + c
- Solve for c
  - c = 3
- The equation is y = 6x + 3

What are the equations of horizontal and vertical lines?

A horizontal line has the equation y = c
- c is the y-intercept
A vertical line has the equation x = k
- k is the x-intercept
For example
- y = 4
- x = -2

Worked Example

(a) Find the equation of the straight line shown in the diagram below.

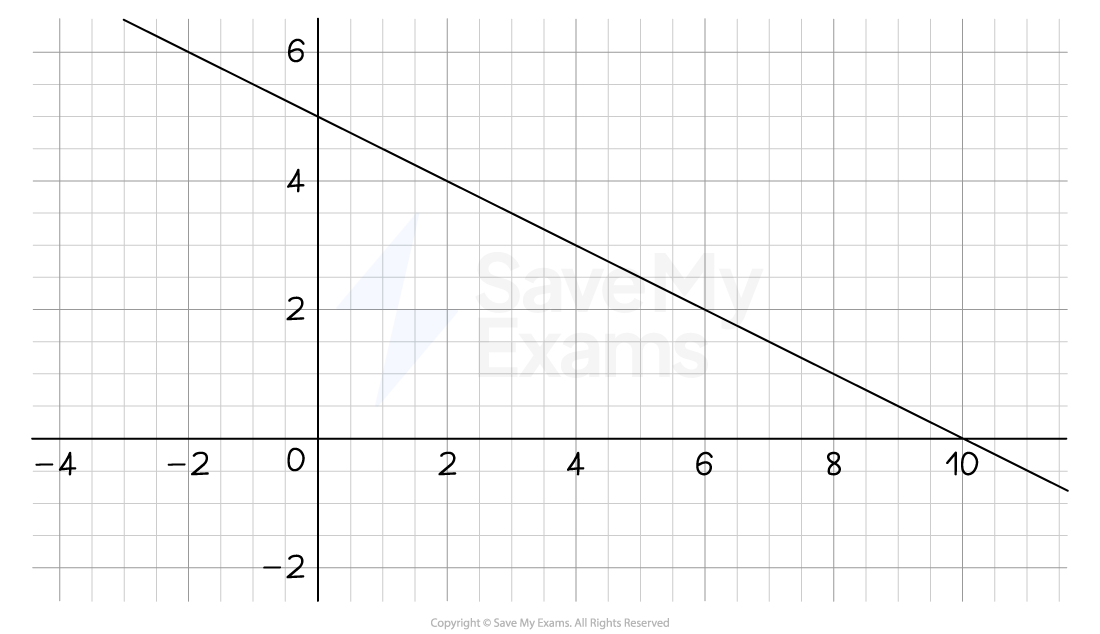
Graph of a straight line with negative gradient

Find m, the gradient
Identify any two points the line passes through and work out the rise and run

Line passes through (2, 4) and (10, 0)

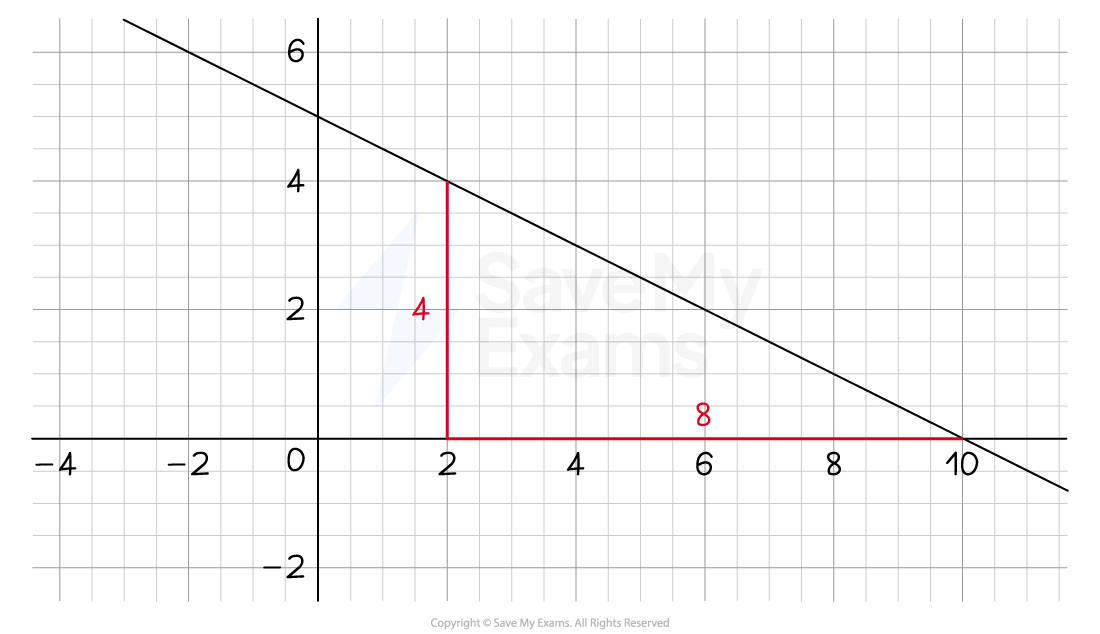
Finding the equation of a straight line from a graph

The rise is 4
The run is 8

Calculate the fraction $rise over run$

$rise over run equals 4 over 8 equals 1 half$

The slope is downward (downhill), so it is a negative gradient

gradient, <img alt=”m equals negative 1 half” data-mathml='<math ><semantics><mrow><mi >m</mi><mo >=</mo><mo >-</mo><mfrac ><mn>1</mn><mn>2</mn></mfrac></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true}</annotation></semantics></math>’ data-type=”working” height=”47″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2247%22%20width%3D%2267%22%20wrs%3Abaseline%3D%2230%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmi%20mathcolor%3D%22%23000000%22%3Em%3C%2Fmi%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%3D%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E-%3C%2Fmo%3E%3Cmfrac%20mathcolor%3D%22%23000000%22%3E%3Cmn%3E1%3C%2Fmn%3E%3Cmn%3E2%3C%2Fmn%3E%3C%2Fmfrac%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math143f4d31b04031e49f5eb18baba’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAAA%2FGhlYWQQC2qxAAACkAAAADZoaGVhCGsXSAAAAsgAAAAkaG10eE2rRkcAAALsAAAADGxvY2EAHTwYAAAC%2BAAAABBtYXhwBT0FPgAAAwgAAAAgbmFtZaBxlY4AAAMoAAABn3Bvc3QB9wD6AAAEyAAAACBwcmVwa1uragAABOgAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0iEv%2F%2FAAAAPSIS%2F%2F%2F%2FxN3wAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAEAgAFVAtUBqwADADAYAbAEELEAA%2FawAzyxAgf1sAE8sQUD5gCxAAATELEABuWxAAETELABPLEDBfWwAjwTIRUhgAJV%2FasBq1YAAQAAAAEAANV4zkFfDzz1AAMEAP%2F%2F%2F%2F%2FWOhNz%2F%2F%2F%2F%2F9Y6E3MAAP8gBIADqwAAAAoAAgABAAAAAAABAAAD6P9qAAAXcAAA%2F7YEgAABAAAAAAAAAAAAAAAAAAAAAwNSAFUDVgCAA1YAgAAAAAAAAAAoAAAAsgAAAPwAAQAAAAMAXgAFAAAAAAACAIAEAAAAAAAEAADeAAAAAAAAABUBAgAAAAAAAAABABIAAAAAAAAAAAACAA4AE

Maths Gcse Edexcel Foundation