WEILAI Online Academic assistant
WEILAI Online Academic assistant
Back to 课程

Maths Gcse Aqa Higher

0% Complete
0/0 Steps
  1. Scatter-Graphs-And-Correlation Aqa Higher
    2 主题
  2. Cumulative-Frequency-And-Box-Plots Aqa Higher
    4 主题
  3. Histograms Aqa Higher
    3 主题
  4. Statistical-Diagrams Aqa Higher
    5 主题
  5. Averages-Ranges-And-Data Aqa Higher
    7 主题
  6. Combined-And-Conditional-Probability Aqa Higher
    3 主题
  7. Tree-Diagrams Aqa Higher
    1 主题
  8. Simple-Probability-Diagrams Aqa Higher
    3 主题
  9. Transformations Aqa Higher
    5 主题
  10. Vectors Aqa Higher
    6 主题
  11. 3D-Pythagoras-And-Trigonometry Aqa Higher
    1 主题
  12. Sine-Cosine-Rule-And-Area-Of-Triangles Aqa Higher
    4 主题
  13. Pythagoras-And-Trigonometry Aqa Higher
    4 主题
  14. Area-And-Volume-Of-Similar-Shapes Aqa Higher
    1 主题
  15. Congruence-Similarity-And-Geometrical-Proof Aqa Higher
    5 主题
  16. Volume-And-Surface-Area Aqa Higher
    3 主题
  17. Circles-Arcs-And-Sectors Aqa Higher
    2 主题
  18. Area-And-Perimeter Aqa Higher
    4 主题
  19. Circle-Theorems Aqa Higher
    7 主题
  20. Bearings-Scale-Drawing-Constructions-And-Loci Aqa Higher
    5 主题
  21. Angles-In-Polygons-And-Parallel-Lines Aqa Higher
    3 主题
  22. Symmetry-And-Shapes Aqa Higher
    6 主题
  23. Exchange-Rates-And-Best-Buys Aqa Higher
    2 主题
  24. Standard-And-Compound-Units Aqa Higher
    5 主题
  25. Direct-And-Inverse-Proportion Aqa Higher
    2 主题
  26. Problem-Solving-With-Ratios Aqa Higher
    2 主题
  27. Ratios Aqa Higher
    3 主题
  28. Sequences Aqa Higher
    4 主题
  29. Transformations-Of-Graphs Aqa Higher
    2 主题
  30. Graphing-Inequalities Aqa Higher
    2 主题
  31. Solving-Inequalities Aqa Higher
    2 主题
  32. Real-Life-Graphs Aqa Higher
    4 主题
  33. Estimating-Gradients-And-Areas-Under-Graphs Aqa Higher
    2 主题
  34. Equation-Of-A-Circle Aqa Higher
    2 主题
  35. Functions Aqa Higher
    3 主题
  36. Forming-And-Solving-Equations Aqa Higher
    3 主题
  37. Graphs-Of-Functions Aqa Higher
    6 主题
  38. Linear-Graphs Aqa Higher
    4 主题
  39. Coordinate-Geometry Aqa Higher
    4 主题
  40. Iteration Aqa Higher
    1 主题
  41. Simultaneous-Equations Aqa Higher
    2 主题
  42. Quadratic-Equations Aqa Higher
    4 主题
  43. Linear-Equations Aqa Higher
    1 主题
  44. Algebraic-Proof Aqa Higher
    1 主题
  45. Rearranging-Formulas Aqa Higher
    2 主题
  46. Algebraic-Fractions Aqa Higher
    4 主题
  47. Completing-The-Square Aqa Higher
    1 主题
  48. Factorising Aqa Higher
    6 主题
  49. Expanding-Brackets Aqa Higher
    3 主题
  50. Algebraic-Roots-And-Indices Aqa Higher
    1 主题
  51. Using-A-Calculator Aqa Higher
    1 主题
  52. Surds Aqa Higher
    2 主题
  53. Rounding-Estimation-And-Bounds Aqa Higher
    2 主题
  54. Fractions-Decimals-And-Percentages Aqa Higher
    3 主题
  55. Introduction Aqa Higher
    7 主题
  56. Simple-And-Compound-Interest-Growth-And-Decay Aqa Higher
    4 主题
  57. Percentages Aqa Higher
    3 主题
  58. Fractions Aqa Higher
    4 主题
  59. Powers-Roots-And-Standard-Form Aqa Higher
    4 主题
  60. Prime-Factors-Hcf-And-Lcm Aqa Higher
    4 主题
  61. Number-Operations Aqa Higher
    10 主题
课 Progress
0% Complete

Exam code:8300

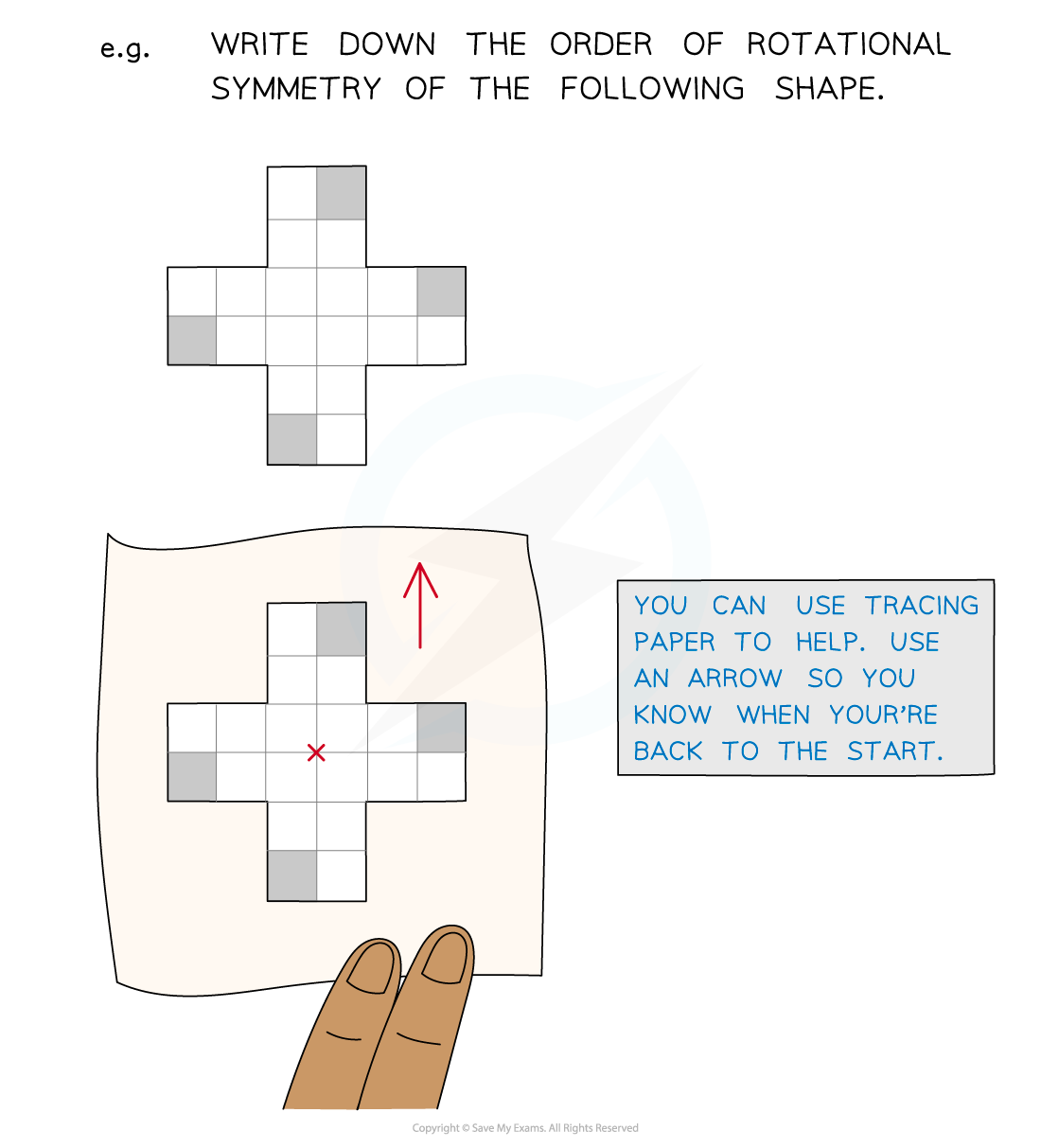
Rotational symmetry

What is the order of rotational symmetry?

  • Rotational symmetry refers to the number of times a shape looks the same as it is rotated 360° about its centre

  • This number is called the order of rotational symmetry

  • Tracing paper can help work out the order of rotational symmetry

    • Draw an arrow on the tracing paper so you can easily tell when you have turned it through 360°

finding the order of rotational symmetry using tracing paper
finding the order of rotational symmetry using tracing paper 2
finding the order of rotational symmetry using tracing paper 3

  • Notice that returning to the original shape contributes 1 to the order

    • This means a shape can never have order 0

    • A shape with rotational symmetry order 1 may be described as not having any rotational symmetry

    • The only time it looks the same is when you get back to the start

Examiner Tips and Tricks

Remember to use the trick above; using an upwards arrow on the tracing paper to show the starting orientation of the shape.

Worked Example

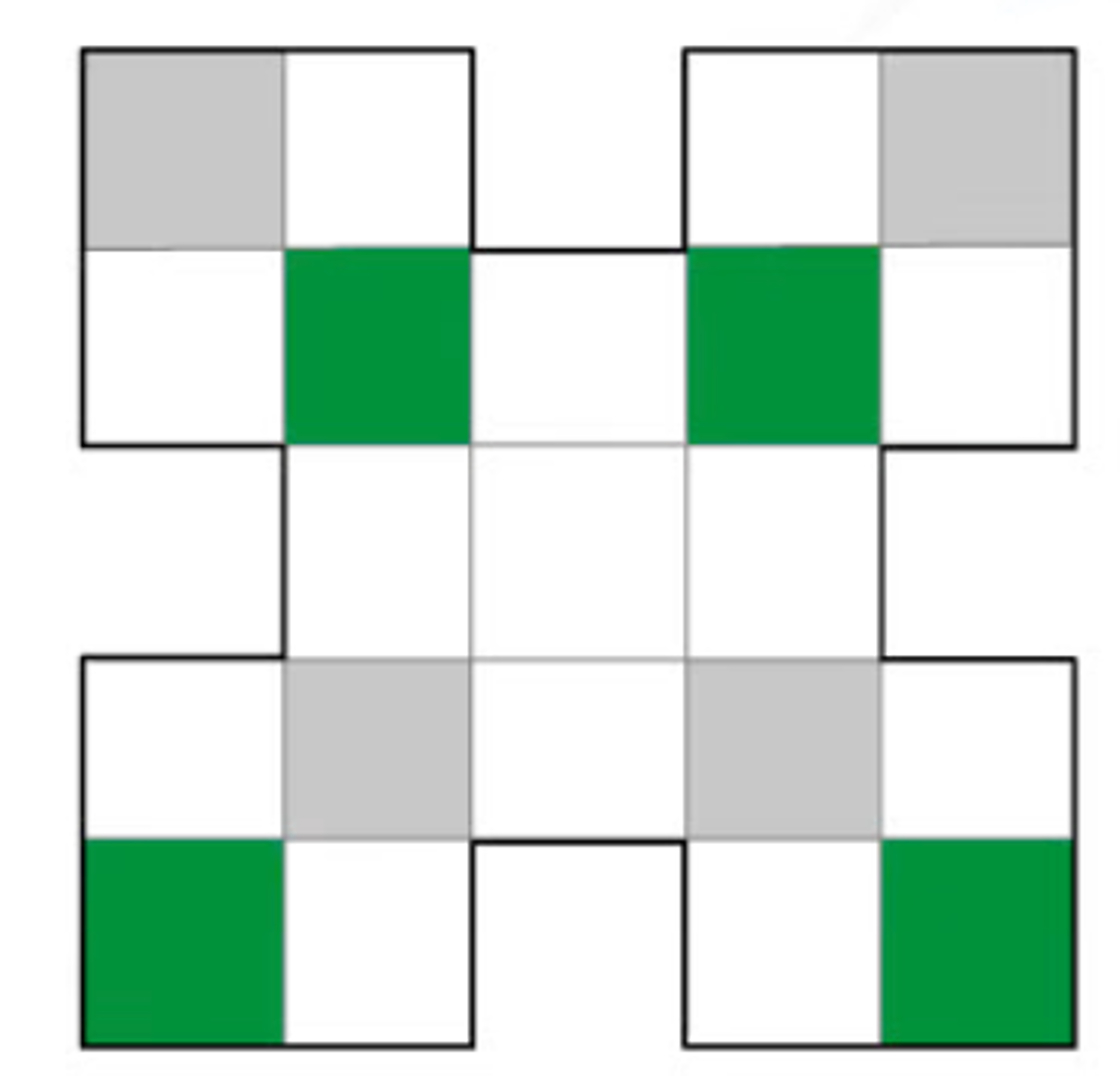
For the shape below, shade exactly 4 more squares so that the shape has rotational symmetry of order 4.

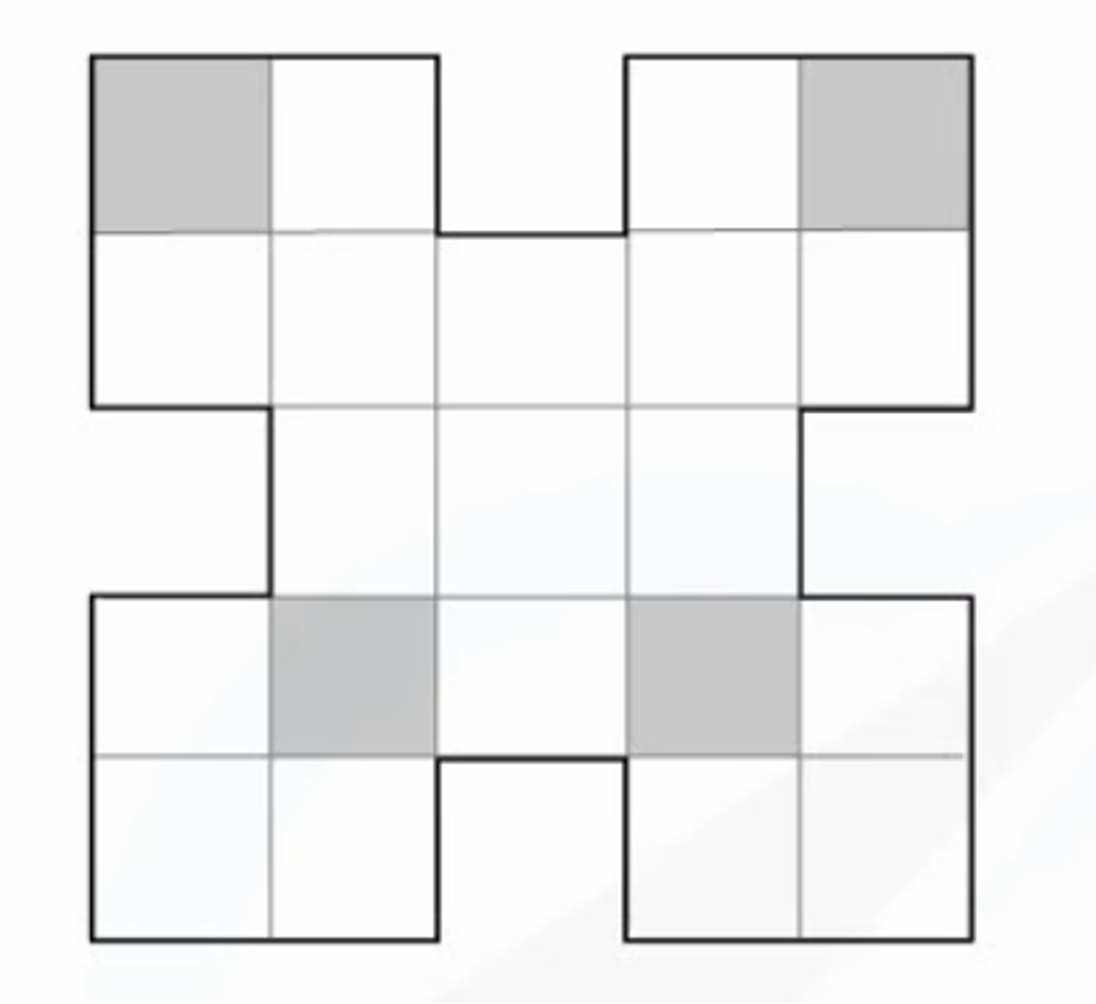
3-1-line-and-rotation-symmetry-we

The shape below appears the same 4 times if rotated through 360 degrees

3-1-1-rotation-symmetry-we-answer

Responses

您的邮箱地址不会被公开。 必填项已用 * 标注