WEILAI Online Academic assistant
WEILAI Online Academic assistant
Back to 课程

Maths Gcse Aqa Higher

0% Complete
0/0 Steps
  1. Scatter-Graphs-And-Correlation Aqa Higher
    2 主题
  2. Cumulative-Frequency-And-Box-Plots Aqa Higher
    4 主题
  3. Histograms Aqa Higher
    3 主题
  4. Statistical-Diagrams Aqa Higher
    5 主题
  5. Averages-Ranges-And-Data Aqa Higher
    7 主题
  6. Combined-And-Conditional-Probability Aqa Higher
    3 主题
  7. Tree-Diagrams Aqa Higher
    1 主题
  8. Simple-Probability-Diagrams Aqa Higher
    3 主题
  9. Transformations Aqa Higher
    5 主题
  10. Vectors Aqa Higher
    6 主题
  11. 3D-Pythagoras-And-Trigonometry Aqa Higher
    1 主题
  12. Sine-Cosine-Rule-And-Area-Of-Triangles Aqa Higher
    4 主题
  13. Pythagoras-And-Trigonometry Aqa Higher
    4 主题
  14. Area-And-Volume-Of-Similar-Shapes Aqa Higher
    1 主题
  15. Congruence-Similarity-And-Geometrical-Proof Aqa Higher
    5 主题
  16. Volume-And-Surface-Area Aqa Higher
    3 主题
  17. Circles-Arcs-And-Sectors Aqa Higher
    2 主题
  18. Area-And-Perimeter Aqa Higher
    4 主题
  19. Circle-Theorems Aqa Higher
    7 主题
  20. Bearings-Scale-Drawing-Constructions-And-Loci Aqa Higher
    5 主题
  21. Angles-In-Polygons-And-Parallel-Lines Aqa Higher
    3 主题
  22. Symmetry-And-Shapes Aqa Higher
    6 主题
  23. Exchange-Rates-And-Best-Buys Aqa Higher
    2 主题
  24. Standard-And-Compound-Units Aqa Higher
    5 主题
  25. Direct-And-Inverse-Proportion Aqa Higher
    2 主题
  26. Problem-Solving-With-Ratios Aqa Higher
    2 主题
  27. Ratios Aqa Higher
    3 主题
  28. Sequences Aqa Higher
    4 主题
  29. Transformations-Of-Graphs Aqa Higher
    2 主题
  30. Graphing-Inequalities Aqa Higher
    2 主题
  31. Solving-Inequalities Aqa Higher
    2 主题
  32. Real-Life-Graphs Aqa Higher
    4 主题
  33. Estimating-Gradients-And-Areas-Under-Graphs Aqa Higher
    2 主题
  34. Equation-Of-A-Circle Aqa Higher
    2 主题
  35. Functions Aqa Higher
    3 主题
  36. Forming-And-Solving-Equations Aqa Higher
    3 主题
  37. Graphs-Of-Functions Aqa Higher
    6 主题
  38. Linear-Graphs Aqa Higher
    4 主题
  39. Coordinate-Geometry Aqa Higher
    4 主题
  40. Iteration Aqa Higher
    1 主题
  41. Simultaneous-Equations Aqa Higher
    2 主题
  42. Quadratic-Equations Aqa Higher
    4 主题
  43. Linear-Equations Aqa Higher
    1 主题
  44. Algebraic-Proof Aqa Higher
    1 主题
  45. Rearranging-Formulas Aqa Higher
    2 主题
  46. Algebraic-Fractions Aqa Higher
    4 主题
  47. Completing-The-Square Aqa Higher
    1 主题
  48. Factorising Aqa Higher
    6 主题
  49. Expanding-Brackets Aqa Higher
    3 主题
  50. Algebraic-Roots-And-Indices Aqa Higher
    1 主题
  51. Using-A-Calculator Aqa Higher
    1 主题
  52. Surds Aqa Higher
    2 主题
  53. Rounding-Estimation-And-Bounds Aqa Higher
    2 主题
  54. Fractions-Decimals-And-Percentages Aqa Higher
    3 主题
  55. Introduction Aqa Higher
    7 主题
  56. Simple-And-Compound-Interest-Growth-And-Decay Aqa Higher
    4 主题
  57. Percentages Aqa Higher
    3 主题
  58. Fractions Aqa Higher
    4 主题
  59. Powers-Roots-And-Standard-Form Aqa Higher
    4 主题
  60. Prime-Factors-Hcf-And-Lcm Aqa Higher
    4 主题
  61. Number-Operations Aqa Higher
    10 主题
课 Progress
0% Complete

Exam code:8300

Sine rule

What is the sine rule?

  • The sine rule is used in non right-angled triangles

    • It allows us to find missing side lengths or angles

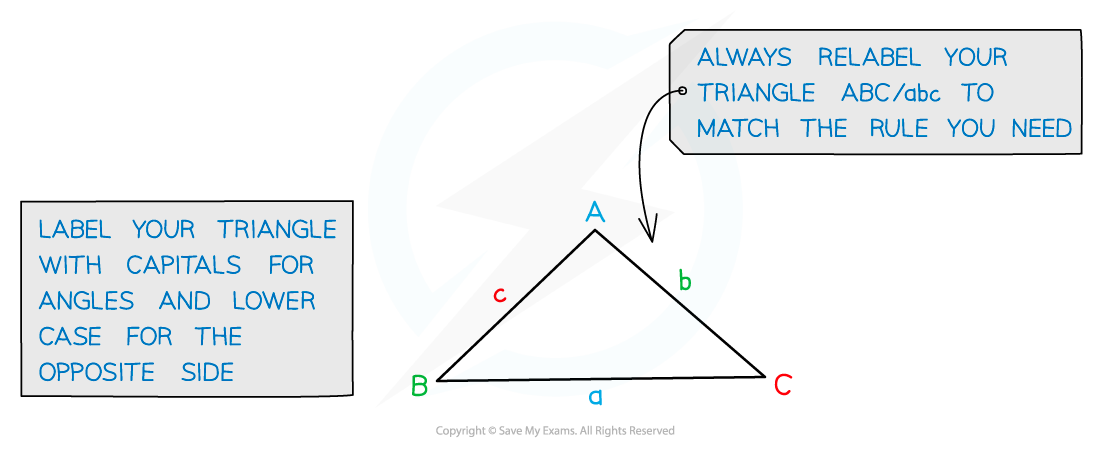
  • It states that for any triangle with angles A, B and C

fraction numerator a over denominator sin space A end fraction equals fraction numerator b over denominator sin space B end fraction equals fraction numerator c over denominator sin space C end fraction

  • Where

    • a is the side opposite angle A

    • b is the side opposite angle B

    • c is the side opposite angle C

Non Right-Angled Triangle labelled with angles A, B and C and opposite corresponding sides a, b and c.

How do I use the sine rule to find missing lengths?

  • Use the sine rule

    • when you have opposite pairs of sides and angles in the question

      • a and A, or b and B, or c and C

  • Start by labelling your triangle with the angles and sides

    • Angles have upper case letters

    • Sides opposite the angles have the equivalent lower case letter

  • To find a missing length, substitute numbers into the formula

    fraction numerator a over denominator sin space A end fraction equals fraction numerator b over denominator sin space B end fraction equals fraction numerator c over denominator sin space C end fraction

    • You only need to have two parts equal to each other (not all three)

      • Then solve to find the side you need

How do I use the sine rule to find missing angles?

  • To find a missing angle, it is easier to rearrange the formula first by flipping each part

    <img alt=”fraction numerator sin space A blank over denominator a end fraction equals blank fraction numerator sin space B blank over denominator b end fraction equals blank fraction numerator sin space C blank over denominator c end fraction” data-mathml='<math ><semantics><mrow><mfrac><mrow><mi>sin</mi><mo> </mo><mi>A</mi><mi> </mi></mrow><mi>a</mi></mfrac><mo>=</mo><mi> </mi><mfrac><mrow><mi>sin</mi><mo> </mo><mi>B</mi><mi> </mi></mrow><mi>b</mi></mfrac><mo>=</mo><mi> </mi><mfrac><mrow><mi>sin</mi><mo> </mo><mi>C</mi><mi> </mi></mrow><mi>c</mi></mfrac></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″}</annotation></semantics></math>’ height=”47″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2247%22%20width%3D%22196%22%20wrs%3Abaseline%3D%2230%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmfrac%3E%3Cmrow%3E%3Cmi%3Esin%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3EA%3C%2Fmi%3E%3Cmi%3E%26%23xA0%3B%3C%2Fmi%3E%3C%2Fmrow%3E%3Cmi%3Ea%3C%2Fmi%3E%3C%2Fmfrac%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmi%3E%26%23xA0%3B%3C%2Fmi%3E%3Cmfrac%3E%3Cmrow%3E%3Cmi%3Esin%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3EB%3C%2Fmi%3E%3Cmi%3E%26%23xA0%3B%3C%2Fmi%3E%3C%2Fmrow%3E%3Cmi%3Eb%3C%2Fmi%3E%3C%2Fmfrac%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmi%3E%26%23xA0%3B%3C%2F

Responses

您的邮箱地址不会被公开。 必填项已用 * 标注