WEILAI Online Academic assistant
WEILAI Online Academic assistant
Back to 课程

Maths Gcse Aqa Higher

0% Complete
0/0 Steps
  1. Scatter-Graphs-And-Correlation Aqa Higher
    2 主题
  2. Cumulative-Frequency-And-Box-Plots Aqa Higher
    4 主题
  3. Histograms Aqa Higher
    3 主题
  4. Statistical-Diagrams Aqa Higher
    5 主题
  5. Averages-Ranges-And-Data Aqa Higher
    7 主题
  6. Combined-And-Conditional-Probability Aqa Higher
    3 主题
  7. Tree-Diagrams Aqa Higher
    1 主题
  8. Simple-Probability-Diagrams Aqa Higher
    3 主题
  9. Transformations Aqa Higher
    5 主题
  10. Vectors Aqa Higher
    6 主题
  11. 3D-Pythagoras-And-Trigonometry Aqa Higher
    1 主题
  12. Sine-Cosine-Rule-And-Area-Of-Triangles Aqa Higher
    4 主题
  13. Pythagoras-And-Trigonometry Aqa Higher
    4 主题
  14. Area-And-Volume-Of-Similar-Shapes Aqa Higher
    1 主题
  15. Congruence-Similarity-And-Geometrical-Proof Aqa Higher
    5 主题
  16. Volume-And-Surface-Area Aqa Higher
    3 主题
  17. Circles-Arcs-And-Sectors Aqa Higher
    2 主题
  18. Area-And-Perimeter Aqa Higher
    4 主题
  19. Circle-Theorems Aqa Higher
    7 主题
  20. Bearings-Scale-Drawing-Constructions-And-Loci Aqa Higher
    5 主题
  21. Angles-In-Polygons-And-Parallel-Lines Aqa Higher
    3 主题
  22. Symmetry-And-Shapes Aqa Higher
    6 主题
  23. Exchange-Rates-And-Best-Buys Aqa Higher
    2 主题
  24. Standard-And-Compound-Units Aqa Higher
    5 主题
  25. Direct-And-Inverse-Proportion Aqa Higher
    2 主题
  26. Problem-Solving-With-Ratios Aqa Higher
    2 主题
  27. Ratios Aqa Higher
    3 主题
  28. Sequences Aqa Higher
    4 主题
  29. Transformations-Of-Graphs Aqa Higher
    2 主题
  30. Graphing-Inequalities Aqa Higher
    2 主题
  31. Solving-Inequalities Aqa Higher
    2 主题
  32. Real-Life-Graphs Aqa Higher
    4 主题
  33. Estimating-Gradients-And-Areas-Under-Graphs Aqa Higher
    2 主题
  34. Equation-Of-A-Circle Aqa Higher
    2 主题
  35. Functions Aqa Higher
    3 主题
  36. Forming-And-Solving-Equations Aqa Higher
    3 主题
  37. Graphs-Of-Functions Aqa Higher
    6 主题
  38. Linear-Graphs Aqa Higher
    4 主题
  39. Coordinate-Geometry Aqa Higher
    4 主题
  40. Iteration Aqa Higher
    1 主题
  41. Simultaneous-Equations Aqa Higher
    2 主题
  42. Quadratic-Equations Aqa Higher
    4 主题
  43. Linear-Equations Aqa Higher
    1 主题
  44. Algebraic-Proof Aqa Higher
    1 主题
  45. Rearranging-Formulas Aqa Higher
    2 主题
  46. Algebraic-Fractions Aqa Higher
    4 主题
  47. Completing-The-Square Aqa Higher
    1 主题
  48. Factorising Aqa Higher
    6 主题
  49. Expanding-Brackets Aqa Higher
    3 主题
  50. Algebraic-Roots-And-Indices Aqa Higher
    1 主题
  51. Using-A-Calculator Aqa Higher
    1 主题
  52. Surds Aqa Higher
    2 主题
  53. Rounding-Estimation-And-Bounds Aqa Higher
    2 主题
  54. Fractions-Decimals-And-Percentages Aqa Higher
    3 主题
  55. Introduction Aqa Higher
    7 主题
  56. Simple-And-Compound-Interest-Growth-And-Decay Aqa Higher
    4 主题
  57. Percentages Aqa Higher
    3 主题
  58. Fractions Aqa Higher
    4 主题
  59. Powers-Roots-And-Standard-Form Aqa Higher
    4 主题
  60. Prime-Factors-Hcf-And-Lcm Aqa Higher
    4 主题
  61. Number-Operations Aqa Higher
    10 主题
课 Progress
0% Complete

Exam code:8300

Speed-time graphs

How do I use a speed-time graph?

  • Kinematics is the study of motion of objects

    • It looks at how an object moves over time

  • Speed-time graphs show the speed of an object at different times

    • Speed is on the vertical axis

    • Time is on the horizontal axis 

  • The gradient of the graph is the acceleration

    • Acceleration space equals space speed over time space equals space rise over run

  • A positive gradient shows positive acceleration (speeding up)

  • A negative gradient shows negative acceleration, (slowing down)

    • This is also called deceleration

Acceleration examples - a car decelerating as it brakes, and a rocket accelerating up towards space

  • Horizontal lines indicate moving at a constant speed

    • The object is neither speeding up or slowing down

    • If the constant speed is zero, then it is at rest

  • A straight line shows constant acceleration

  • A curve shows changing acceleration

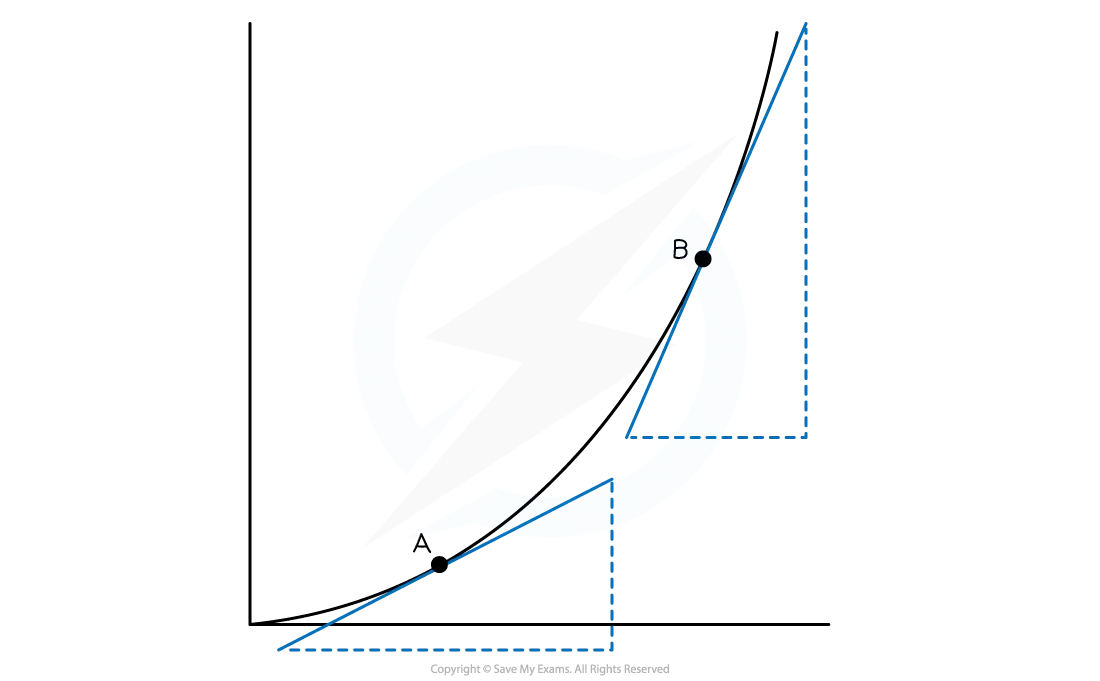
    • To find the acceleration at a particular point on the graph

      • draw a tangent to the graph at this point and find its gradient

A graph showing tangents drawn at two points, A and B, on a curve. The tangent at point A has a shallow gradient and the tangent at point B has a steeper gradient.

  • The distance covered by the object is the area under the graph

    • Split the area into simple shapes, e.g. rectangles and triangles

    • Find the area of each shape and add them together

Examiner Tips and Tricks

  • Always check the vertical axis to see if you are given a speed-time graph or a distance-time graph!

Worked Example

The speed-time graph for a car travelling between two sets of traffic lights is shown below. 

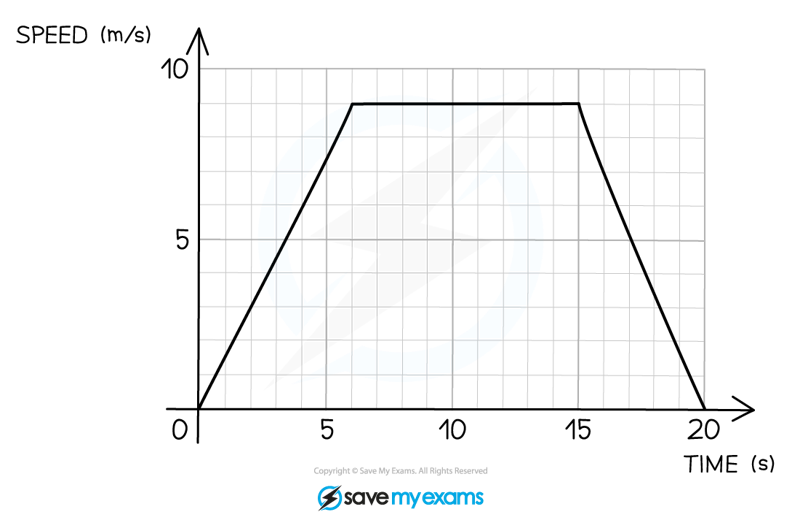
real-life-graphs-s-t-graph-we-image

(a) For how long was the car travelling at a constant speed?

Constant speed is represented by horizontal lines

There is a horizontal line from 6 seconds to 15 seconds

15 – 6 = 9

9 seconds

(b) Calculate the acceleration during the first 6 seconds. 

In a speed-time graph the acceleration is the gradient of the graph

acceleration space equals space fraction numerator space rise over denominator run end fraction equals space speed over time

<img alt=”real-life-graphs-s-t-graph-we-image-2″ class=”ContentBlock_figure__vJw2q” data-nimg=”1″ decoding=”async” height=”1787″ loading=”lazy” sizes=”(max-width: 320px) 320w, (max-width: 640px) 640w, (max-width: 960px) 960w

Responses

您的邮箱地址不会被公开。 必填项已用 * 标注