WEILAI Online Academic assistant
WEILAI Online Academic assistant
Back to 课程

Maths Gcse Aqa Higher

0% Complete
0/0 Steps
  1. Scatter-Graphs-And-Correlation Aqa Higher
    2 主题
  2. Cumulative-Frequency-And-Box-Plots Aqa Higher
    4 主题
  3. Histograms Aqa Higher
    3 主题
  4. Statistical-Diagrams Aqa Higher
    5 主题
  5. Averages-Ranges-And-Data Aqa Higher
    7 主题
  6. Combined-And-Conditional-Probability Aqa Higher
    3 主题
  7. Tree-Diagrams Aqa Higher
    1 主题
  8. Simple-Probability-Diagrams Aqa Higher
    3 主题
  9. Transformations Aqa Higher
    5 主题
  10. Vectors Aqa Higher
    6 主题
  11. 3D-Pythagoras-And-Trigonometry Aqa Higher
    1 主题
  12. Sine-Cosine-Rule-And-Area-Of-Triangles Aqa Higher
    4 主题
  13. Pythagoras-And-Trigonometry Aqa Higher
    4 主题
  14. Area-And-Volume-Of-Similar-Shapes Aqa Higher
    1 主题
  15. Congruence-Similarity-And-Geometrical-Proof Aqa Higher
    5 主题
  16. Volume-And-Surface-Area Aqa Higher
    3 主题
  17. Circles-Arcs-And-Sectors Aqa Higher
    2 主题
  18. Area-And-Perimeter Aqa Higher
    4 主题
  19. Circle-Theorems Aqa Higher
    7 主题
  20. Bearings-Scale-Drawing-Constructions-And-Loci Aqa Higher
    5 主题
  21. Angles-In-Polygons-And-Parallel-Lines Aqa Higher
    3 主题
  22. Symmetry-And-Shapes Aqa Higher
    6 主题
  23. Exchange-Rates-And-Best-Buys Aqa Higher
    2 主题
  24. Standard-And-Compound-Units Aqa Higher
    5 主题
  25. Direct-And-Inverse-Proportion Aqa Higher
    2 主题
  26. Problem-Solving-With-Ratios Aqa Higher
    2 主题
  27. Ratios Aqa Higher
    3 主题
  28. Sequences Aqa Higher
    4 主题
  29. Transformations-Of-Graphs Aqa Higher
    2 主题
  30. Graphing-Inequalities Aqa Higher
    2 主题
  31. Solving-Inequalities Aqa Higher
    2 主题
  32. Real-Life-Graphs Aqa Higher
    4 主题
  33. Estimating-Gradients-And-Areas-Under-Graphs Aqa Higher
    2 主题
  34. Equation-Of-A-Circle Aqa Higher
    2 主题
  35. Functions Aqa Higher
    3 主题
  36. Forming-And-Solving-Equations Aqa Higher
    3 主题
  37. Graphs-Of-Functions Aqa Higher
    6 主题
  38. Linear-Graphs Aqa Higher
    4 主题
  39. Coordinate-Geometry Aqa Higher
    4 主题
  40. Iteration Aqa Higher
    1 主题
  41. Simultaneous-Equations Aqa Higher
    2 主题
  42. Quadratic-Equations Aqa Higher
    4 主题
  43. Linear-Equations Aqa Higher
    1 主题
  44. Algebraic-Proof Aqa Higher
    1 主题
  45. Rearranging-Formulas Aqa Higher
    2 主题
  46. Algebraic-Fractions Aqa Higher
    4 主题
  47. Completing-The-Square Aqa Higher
    1 主题
  48. Factorising Aqa Higher
    6 主题
  49. Expanding-Brackets Aqa Higher
    3 主题
  50. Algebraic-Roots-And-Indices Aqa Higher
    1 主题
  51. Using-A-Calculator Aqa Higher
    1 主题
  52. Surds Aqa Higher
    2 主题
  53. Rounding-Estimation-And-Bounds Aqa Higher
    2 主题
  54. Fractions-Decimals-And-Percentages Aqa Higher
    3 主题
  55. Introduction Aqa Higher
    7 主题
  56. Simple-And-Compound-Interest-Growth-And-Decay Aqa Higher
    4 主题
  57. Percentages Aqa Higher
    3 主题
  58. Fractions Aqa Higher
    4 主题
  59. Powers-Roots-And-Standard-Form Aqa Higher
    4 主题
  60. Prime-Factors-Hcf-And-Lcm Aqa Higher
    4 主题
  61. Number-Operations Aqa Higher
    10 主题
课 Progress
0% Complete

Exam code:8300

Prime factor decomposition

What are prime factors?

  • A factor of a given number is a value that divides the given number exactly, with no remainder

    • e.g. 6 is a factor of 18

  • A prime number is a number which has exactly two factors; itself and 1

    • e.g. 5 is a prime number, as its only factors are 5 and 1

    • You should remember the first few prime numbers:

      • 2, 3, 5, 7, 11, 13, 17, 19, …

  • The prime factors of a number are therefore all the primes which multiply to give that number

    • e.g. The prime factors of 30 are 2, 3, and 5

      • 2 × 3 × 5 = 30

How do I find prime factors?

  • Use a factor tree to find prime factors

    • Split the number up into a pair of factors

    • Then split each of those factors up into another pair

    • Continue splitting up factors along each “branch” until you get to a prime number

      • These can not be split into anything other than 1 and themselves

      • It helps to circle the prime numbers at the end of the branches

Prime factors of 360 in a factor tree

  • A number can be uniquely written as a product of prime factors

    • Write the prime factors as a multiplication, in ascending order

      • 360 = 2 × 2 × 2 × 3 × 3 × 5

    • This can then be written more concisely using powers

      • 360 = 23 × 32 × 5

  • A question asking you to do this will usually be phrased as “Express … as the product of its prime factors”

Worked Example

Write 432 as the product of its prime factors.

Create a factor tree
Start with 432 and choose any two numbers that multiply together to make 432

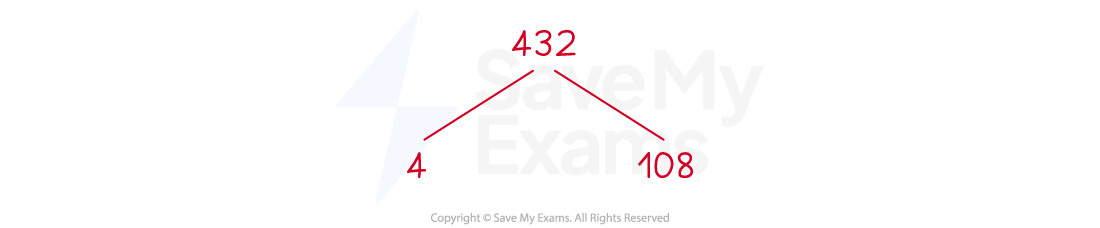
igcse-core-maths-oct-19-paper-3-q4g-1

Repeat this for the two factors, until all of the values are prime numbers and cannot be broken down any further

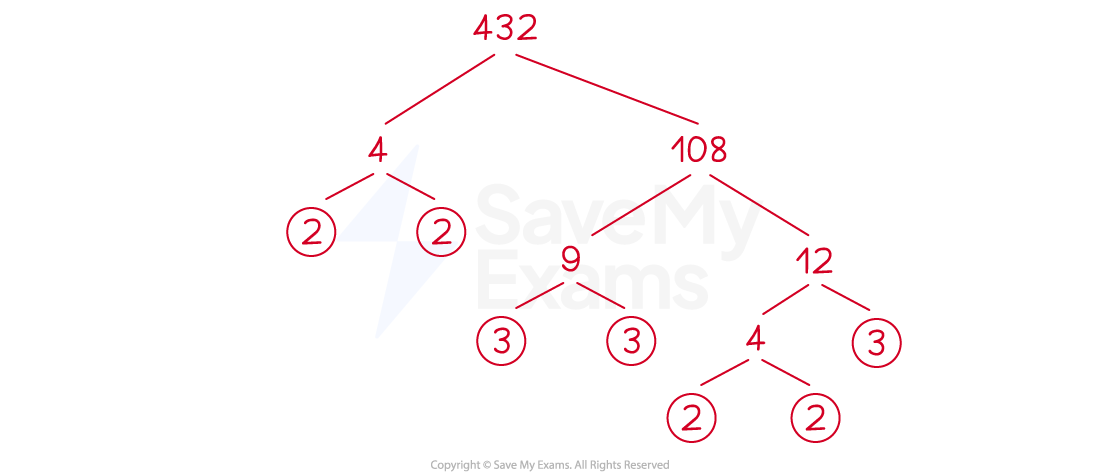
igcse-core-maths-oct-19-paper-3-q4g-2

The answer will be the same regardless of the factors chosen in the first step

Write the prime numbers out as a product

432 equals space 2 space cross times space 2 space cross times space 2 space cross times space 2 space cross times space 3 space cross times space 3 space cross times space 3

Any repeated prime factors can be written as a power

<img alt=”432 space equals space bold 2 to the power of bold 4 bold space bold cross times bold space bold 3 to the power of bold 3 bold space” data-mathml='<math ><semantics><mrow><mn >432</mn><mo >&#160;</mo><mo >=</mo><mo >&#160;</mo><msup><mn mathvariant=”bold” >2</mn><mn mathvariant=”bold” >4</mn></msup><mo mathvariant=”bold” >&#160;</mo><mo mathvariant=”bold” >&#215;</mo><mo mathvariant=”bold” >&#160;</mo><msup><mn mathvariant=”bold” >3</mn><mn mathvariant=”bold” >3</mn></msup><mo mathvariant=”bold” >&#160;</mo></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true}</annotation></semantics></math>’ data-type=”finalAnswer” height=”23″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2223%22%20width%3D%22120%22%20wrs%3Abaseline%3D%2217%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmn%20mathcolor%3D%22%23000000%22%3E432%3C%2Fmn%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%3D%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmsup%3E%3Cmn%20mathcolor%3D%22%23000000%22%20mathvariant%3D%22bold%22%3E2%3C%2Fmn%3E%3Cmn%20mathcolor%3D%22%23000000%22%20mathvariant%3D%22bold%22%3E4%3C%2Fmn%3E%3C%2Fmsup%3E%3Cmo%20mathcolor%3D%22%23000000%22%20mathvariant%3D%22bold%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000000%22%20mathvariant%3D%22bold%22%3E%26%23xD7%3B%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000000%22%20mathvariant%3D%22bold%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmsup%3E%3Cmn%20mathcolor%3D%22%23000000%22%20mathvariant%3D%22bold%22%3E3%3C%2Fmn%3E%3Cmn%20mathcolor%3D%22%23000000%22%20mathvariant%3D%22bold%22%3E3%3C%2Fmn%3E%3C%2Fmsup%3E%3Cmo%20mathcolor%3D%22%23000000%22%20mathvariant%3D%22bold%22%3E%26%23xA0%3B%3C%2Fmo%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math102a87acd26f5771b4d57a7dfb3’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAABIWhlYWQQC2qxAAACuAAAADZoaGVhCGsXSAAAAvAAAAAkaG10eE2rRkcAAAMUAAAADGxvY2EAHTwYAAADIAAAABBtYXhwBT0FPgAAAzAAAAAgbmFtZaBxlY4AAANQAAABn3Bvc3QB9wD6AAAE8AAAACBwcmVwa1uragAABRAAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0A1%2F%2F%2FAAAAPQDX%2F%2F%2F%2FxP8rAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMAB

Responses

您的邮箱地址不会被公开。 必填项已用 * 标注