Basic-Probability Aqa Foundation

Basic probability

What is probability?

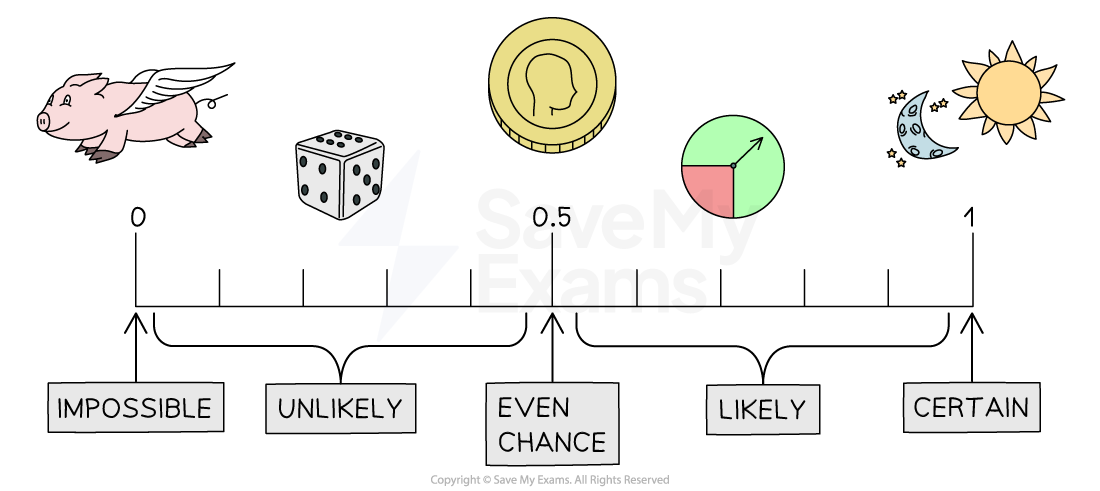
• Probability describes the likelihood of something happening

  • In real-life you might use words such as impossible, unlikely and certain

• In maths we use the probability scale to describe probability

  • This means giving it a number between 0 and 1

    • 0 means impossible

    • Between 0 and 0.5 means unlikely

    • 0.5 means even chance

    • Between 0.5 and 1 means likely

    • 1 means certain

• Probabilities can be given as fractions, decimals or percentages

What key words and terminology are used in probability?

• An experiment is an activity that is repeated to produce a set of results

  • Results can be observed (seen) or recorded

  • Each repeat is called a trial

• An outcome is a possible result of a trial

• An event is an outcome (or a collection of outcomes)

  • For example:

    • a dice lands on a six

    • a dice lands on an even number

  • Events are usually given capital letters

  • n(A) is the number of possible outcomes from event A

    • A = a dice lands on an even number (2, 4 or 6)

    • n(A) = 3 

• A sample space is the set of all possible outcomes of an experiment

  • It can be represented as a list or a table

• The probability of event A is written P(A)

• An event is said to be fair if there is an equal chance of achieving each outcome

  • If there is not an equal chance, the event is biased

  • For example, a fair coin has an equal chance of landing on heads or tails

How do I calculate basic probabilities?

• If all outcomes are equally likely then the probability for each outcome is the same

  • The probability for each outcome is

    • If there are 50 marbles in a bag then the probability of selecting a specific one is

• The theoretical probability of an event can be calculated by dividing the number of outcomes of that event by the total number of outcomes

  •  

  • This can be calculated without actually doing the experiment 

• If there are 50 marbles in a bag and 20 are blue, then the probability of selecting a blue marble is

How do I find missing probabilities?

• The probabilities of all the outcomes add up to 1

  • If you have a table of probabilities with one missing, find it by making them all add up to 1 

• The complement of event A is the event where A does not happen

  • This can be thought of as not A

  • P(event does not happen) = 1 – P(event does happen)

    • For example, if the probability of rain is 0.3, then the probability of not rain is 1 – 0.3 = 0.7

What are mutually exclusive events?

• Two events are mutually exclusive if they cannot both happen at once

  • When rolling a dice, the events “getting a prime number” and “getting a 6” are mutually exclusive

• If A and B are mutually exclusive events, then the probability of either A or B happening is P(A) + P(B)

• Complementary events are mutually exclusive