Finding an upper bound using a minimum connector
Why do I need to find an upper bound?
-
There is no efficient algorithm to find the optimal solution for the travelling salesman problem
-
An upper and lower bound for the solution to the problem can be found
-
The optimal solution (the shortest route) will lie within these bounds
-
-
The aim is to find the minimum value for the upper bound to reduce the size of interval between the upper and lower bounds
How do I find the upper bound?
-
You can find an upper bound for the practical travelling salesman problem using the minimum spanning tree of a network
-
STEP 1 Find the minimum spanning tree for the network using either Prim’s or Kruskal’s algorithm
-
If you have the table of least distances – use Prim’s algorithm
-
If you have the graph only – use Kruskal’s algorithm
-
-
STEP 2 Double the weight of the minimum spanning tree
-
Each vertex can therefore definitely be visited and the starting vertex returned to
-
-
STEP 3 Reduce the weight of the upper bound by finding shortcuts
-
Use some of the edges that are not included in the minimum spanning tree to reduce the weight of the upper bound
-
Worked Example
The network below contains six vertices representing villages and the edges (roads) that connect them. The weighting of the edges represents the time, in minutes, that it takes to walk along a particular road between two villages.

a) Find an initial upper bound for the travelling salesman problem.
-
STEP 1
The question contains the graph but you have not been asked to find the table of least distances, so apply Kruskal’s algorithm to find the minimum spanning tree of the network
List the edges in order of increasing weight
CD (5)
CE (6)
AC (7)
EF (8)
BF (9)
DE (10)
AD (11)
BC (13)
BE (13)
AB (14)
DF (20)
Add the edge of least weight (CD), then the next edge of least weight (CE) Repeat adding the next edge of least weight each time provided it does not create a cycle until all vertices are connected
Edges added in the order: CD (5), CE (6), AC (7), EF (8), BF (9)

-
STEP 2
Find the weight of the minimum spanning tree
5 + 6 + 7 + 8 + 9 = 35
Double the weight of the minimum spanning tree to find the initial upper bound of the solution
35 x 2 = 70
Initial upper bound = 70 minutes
b) Show that the initial upper bound can be reduced to 54 by finding one shortcut.
-
STEP 3
Identify which edges could be used to replace repeated edges in the minimum spanning tree
Single edge: AB (14)
Repeated pathway: AC + CE + EF + FB (30)
Subtract the weight of the single edge from the repeated pathway to calculate the weight saved by using the short cut
30 – 14 = 16
Subtract the weight saving from the initial upper bound
70 – 16 = 54
Improved upper bound = 54 minutes
This can also be seen as 70 – 30 + 14 = 54 (subtract the ‘repeated pathway’, then add the ‘shortcut’)
Finding a lower bound using a minimum connector
Why do I need to find the lower bound?
-
There is no efficient algorithm to find the optimal solution for the travelling salesman problem
-
An upper and lower bound for the solution to the problem can be found
-
The optimal solution (the shortest route) will lie within these bounds
-
-
The aim is to find the maximum value for the lower bound to reduce the size of interval between the upper and lower bounds
-
An optimal solution is found if
-
the lower bound gives a Hamiltonian cycle
-
the lower bound has the same value as the upper bound
-
How do I find the lower bound?
-
You can find a lower bound for the classical travelling salesman problem using the minimum spanning tree of a network
-
To find a solution for the practical travelling salesman problem you need to apply the steps of the algorithm below to a table of least distances
-
-
STEP 1
Remove a vertex and all of its associated edges from the network -
STEP 2
Find the minimum spanning tree for the remaining network and write down its total weight-
This spanning tree is known as the residual minimum spanning tree (RMST)
-
-
STEP 3
Identify the two shortest individual edges that can connect the missing vertex to the residual minimum spanning tree Calculate the sum of the total weight of the residual minimal spanning tree and the two connecting edges -
STEP 4
Repeat Steps 1 to 3 for each vertex in the network -
STEP 5
When the network has been tested for each missing vertex, identify the maximum value-
This maximum value is the greatest possible lower bound
-
-
In many problems Steps 4 and 5 will not be required as a question will dictate which vertex to delete and there will be no need to do them all
-
This method may be referred to as the deleted vertex method
Worked Example
The table below contains six vertices representing villages and the roads that connect them. The weighting of the edges represents the time in minutes that it takes to walk along a particular road between two villages.
|
|
A |
B |
C |
D |
E |
F |
|
A |
– |
14 |
7 |
11 |
13 |
21 |
|
B |
14 |
– |
13 |
18 |
13 |
9 |
|
C |
7 |
13 |
– |
5 |
6 |
14 |
|
D |
11 |
18 |
5 |
– |
10 |
18 |
|
E |
13 |
13 |
6 |
10 |
– |
8 |
|
F |
21 |
9 |
14 |
18 |
8 |
– |
a) By deleting vertex A and using Prim’s algorithm, find a lower bound for the time taken to start at village A, visit each of the other villages and return to village A
-
STEP 1
Delete vertex A in the table -
STEP 2
Perform Prim’s algorithm on the remaining vertices in the table
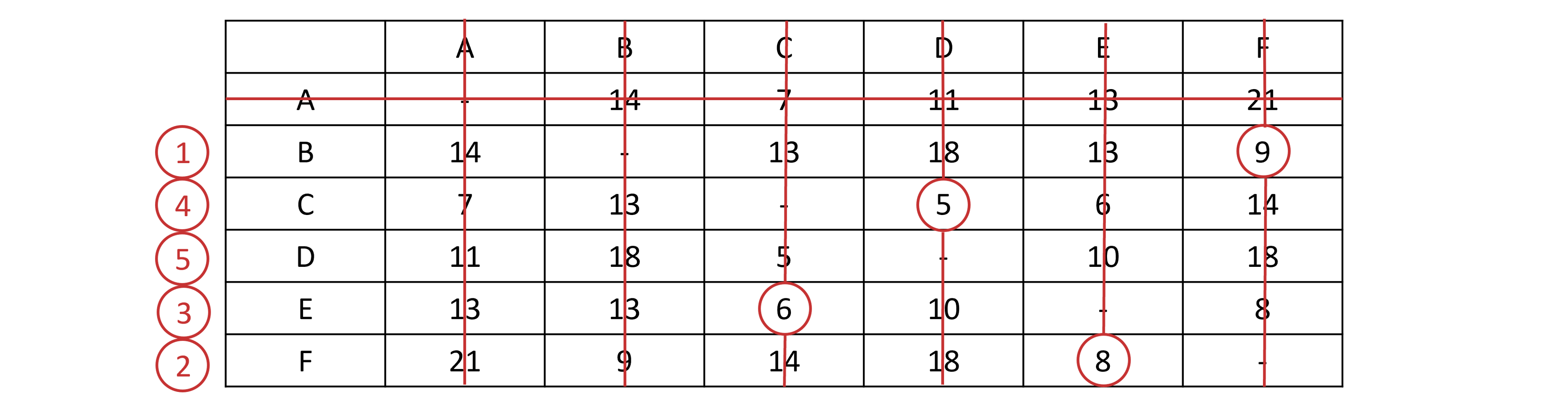
Edges added in the order: BF (9), EF (8), CE (6), CD (5)
Total weight of the residual minimum spanning tree = 9 + 8 + 6 + 5 = 28
-
STEP 3
Identify the two shortest edges that connect A to the minimum spanning tree
AC (7), AD (11)
Add together the total weight of the minimum spanning tree and the weights of the two shortest lengths connecting it to A
28 + 7 + 11 = 46
Lower bound = 46 minutes
b) Show that by deleting vertex E instead, a higher lower bound can be found.
-
STEP 1
Delete vertex E in the table -
STEP 2
Perform Prim’s algorithm on the remaining vertices in the table

Responses