Dummies
What is a dummy activity?
-
A dummy activity is an activity that has a weight of zero
-
dummies are not assigned names (letters)
-
dummies are represented by dotted lines
-
-
Dummies are used to show precedences in more complicated activity networks
When and where are dummies used in an activity network?
-
Two situations can lead to the need for a dummy activity
-
The first situation is to ensure each activity (arc) has a unique pair of start and end nodes
-
e.g. in the activity network below, activity D has immediate predecessors B and C
-
but B and C cannot both start at event/node 1 and end at event/node 2 (this would not be a unique pair)
-
a dummy activity is used so that B has start/end pair (1, 3) and C has start/end pair (1, 2)
-
-

-
Note that the dummy could also go from event 2 to event 3 with activity D commencing from event 3
-
The second situation that requires a dummy is when there is a split of immediate predecessors
-
e.g. in the activity network below, activity D has immediate predecessors B and C
-
but activity E only has B as an immediate predecessor
-
a dummy activity is used to show that D depends on both B and C
-
-

Examiner Tips and Tricks
-
Exam questions will not always require you to draw the whole activity network
-
a diagram of part of the network may be given
-
-
Exam questions are often specific about the number of dummies you should use
-
if you think you need more, go back to see if you can make improvements
-
it is generally expected that an activity network is as concise/efficient as possible with the minimum use of dummies
-
Worked Example
The activities involved in a project are listed in the precedence table below.
|
Activity |
Immediately preceding activities |
Duration (days) |
|
A |
– |
5 |
|
B |
– |
4 |
|
C |
A |
7 |
|
D |
B |
3 |
|
E |
A, D |
7 |
|
F |
B |
6 |
|
G |
C |
6 |
|
H |
C |
4 |
|
I |
G, H |
5 |
|
J |
E, F |
4 |
The project is also represented on the partially completed activity network below.
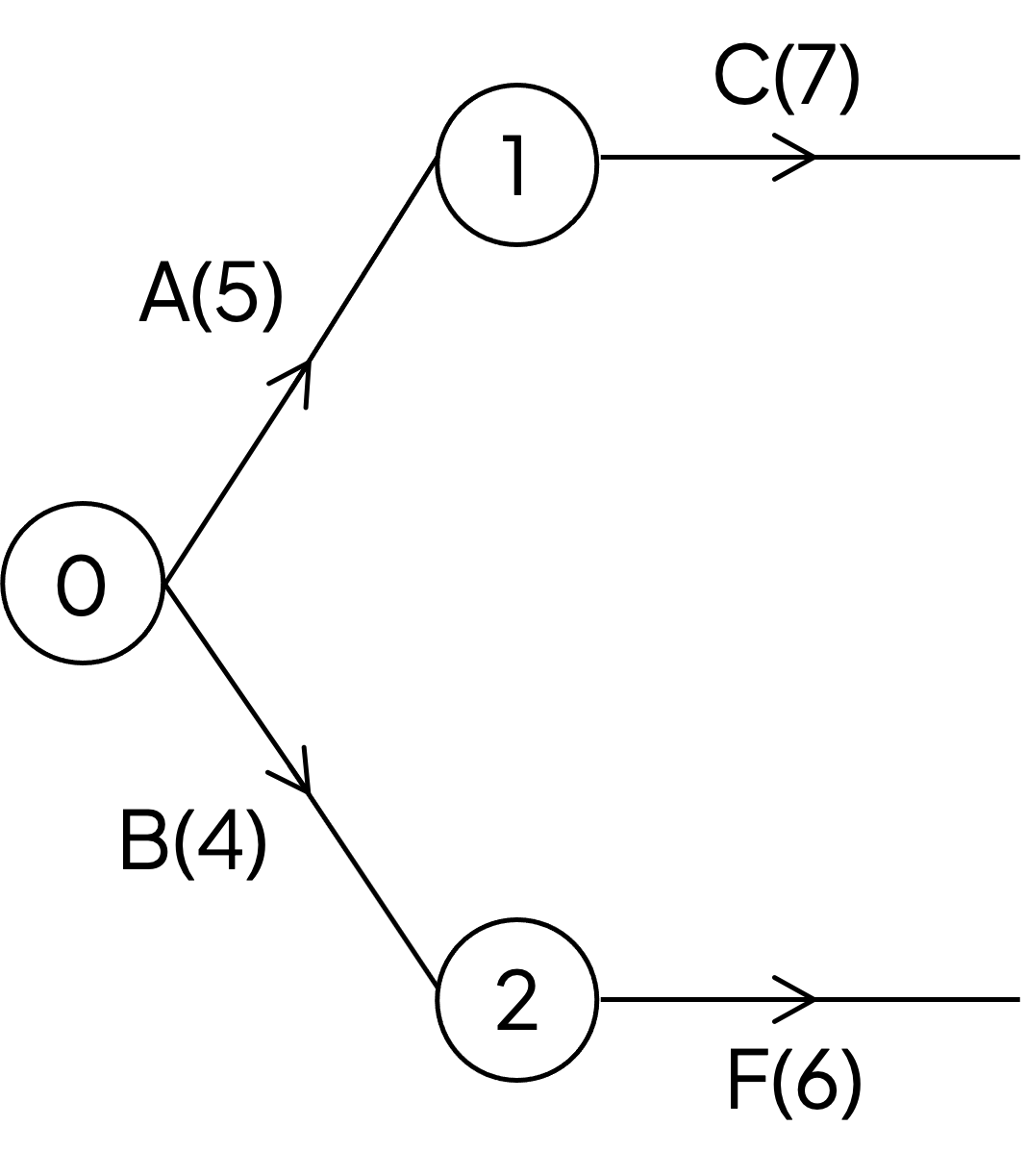
Using exactly two dummy activities, complete the activity network by adding activities D, E, G, H, I and J.
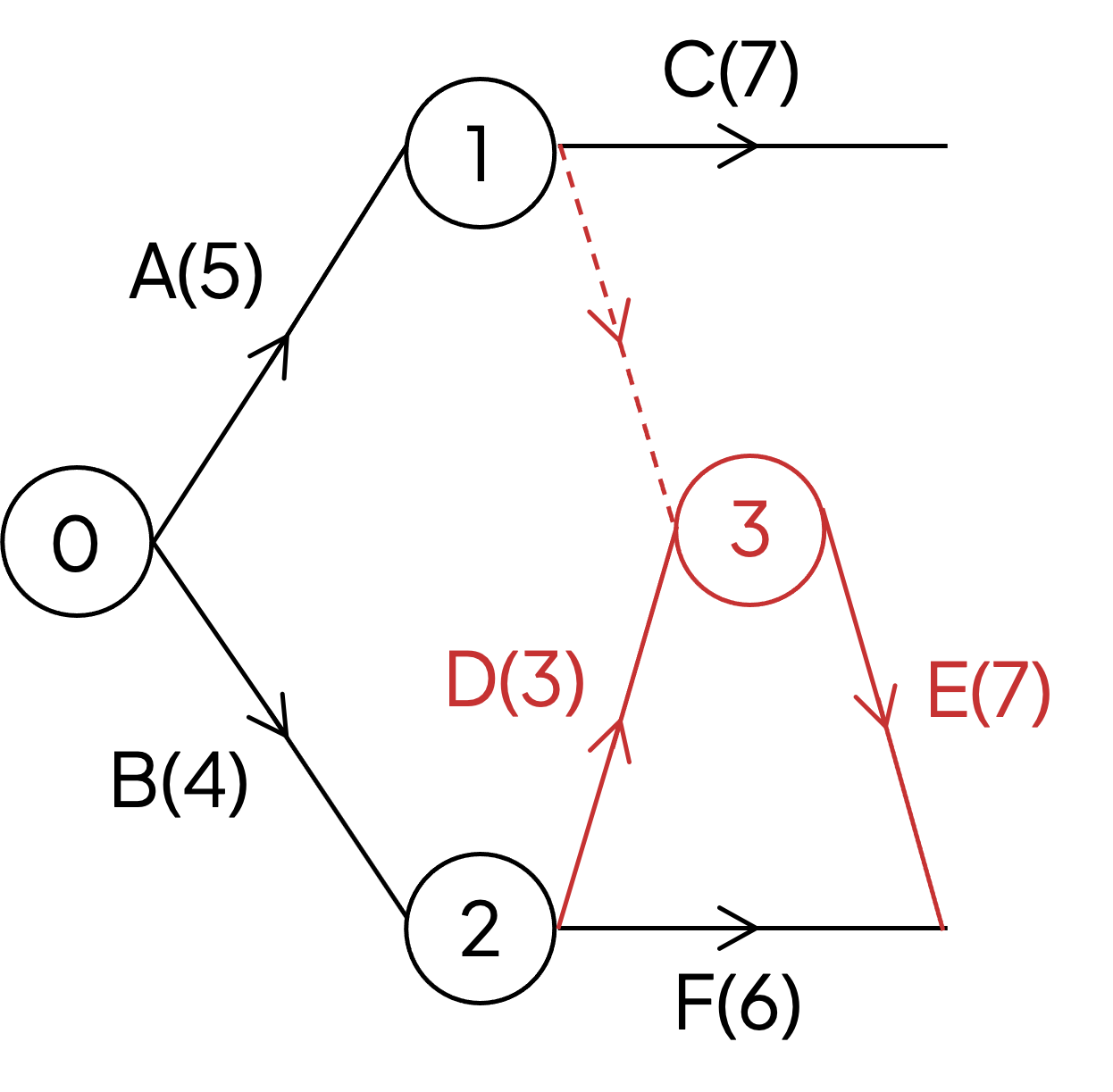
Activity D is dependent on activity B so draw an arc from event/node 2 for D
Looking ahead, activity E is dependent on both A and D, whereas activity C is dependent on just A
This is the second situation (‘split predecessors’) for the use of a dummy activity
Also from looking ahead activity J depends on both E and F – so the arcs for E and F will need to meet
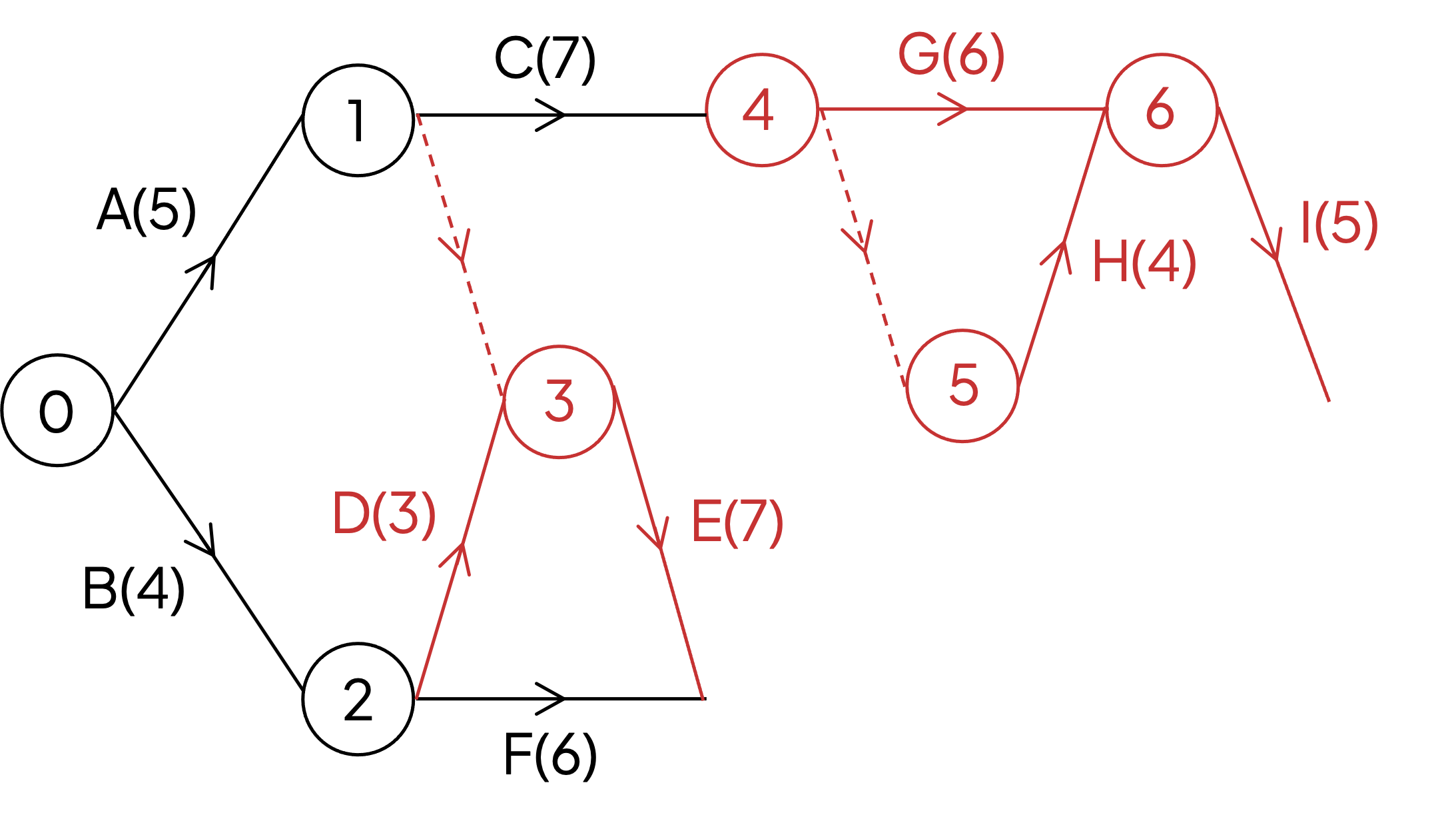
Activities G and H are both dependent on C, and activity I is dependent on both G and H
This could lead to G and H having the same start/end node pair
This is the first situation (‘unique start/end node pair’) for the use of a dummy activity
No activities depend on I so its arc can be drawn to the end of the project (sink node)
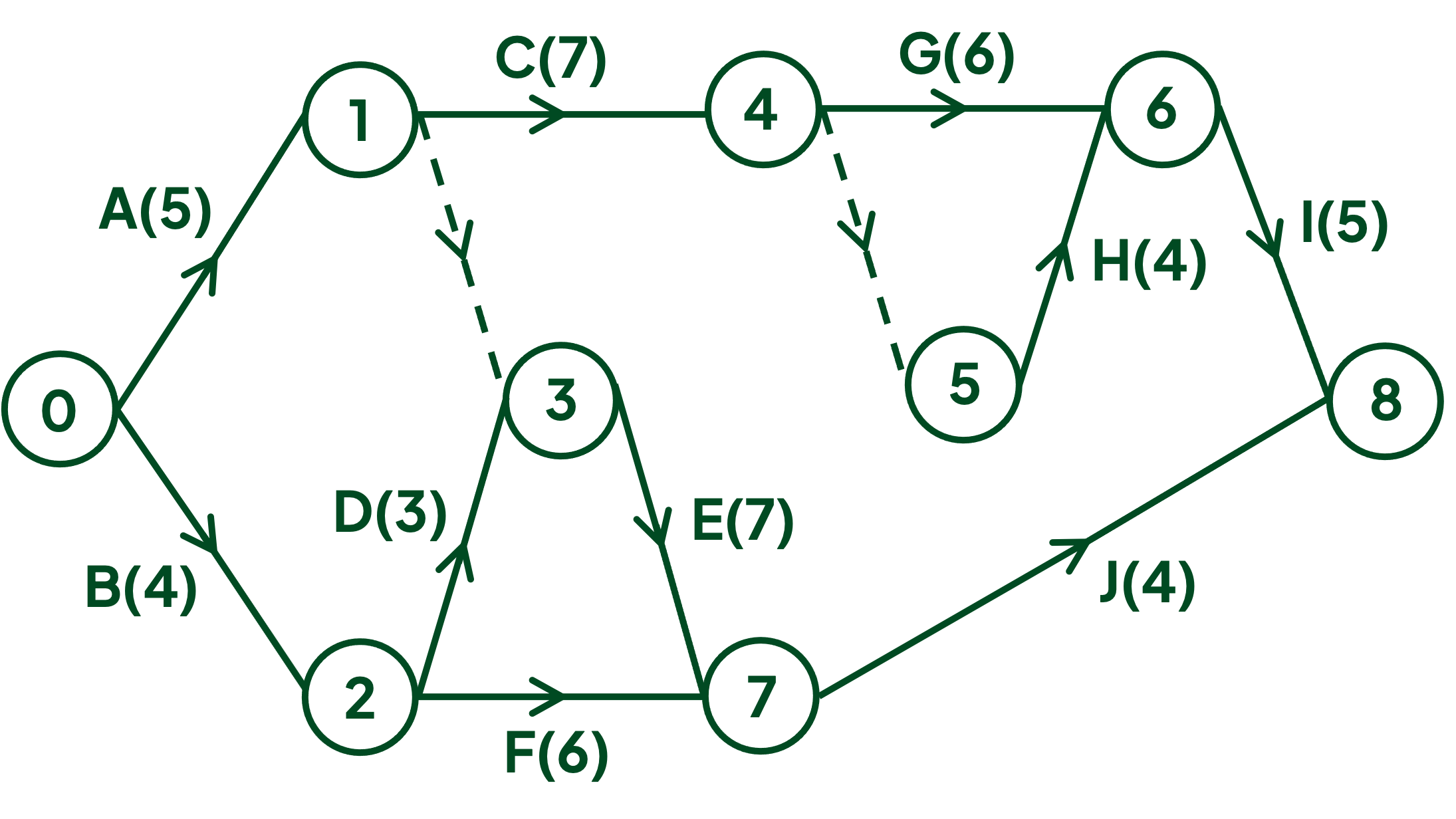
The activity network can now be completed with activity J and the sink node

Responses