problem-solving-with-drvs

课 Progress

0% Complete

Problem solving with DRVs

How do I find DRVs from worded contexts?

Introduce a capital letter, $X$ , to represent numerical values
- Make sure you know exactly what $X$ represents
List all the values $X$ can take
Calculate the probability for each value of $X$
Put this information into a table
$x$
…
$P (X = x)$
…
If asked to comment on results
- Find $E (X)$ to talk about the average result
- Find $Var (X)$ to talk about the spread of results

What if they introduce a new independent variable?

Sometimes questions have two independent DRVs, $X$ and $Y$
- e.g. $X$ may be a coin and $Y$ may be a 3-sided spinner
Construct their tables
$x$
2
4
$P (X = x)$
0.25
0.75
$y$
0
2
4
$P (Y = y)$
0.1
0.2
0.7
To find $P (X + Y = 4)$
- List possibilities
  - $X = 2, Y = 2$ or $X = 4, Y = 0$
- Multiply probabilities then add
  - 0.25 × 0.2 + 0.75 × 0.1
To find $E (X + Y)$
- Either construct a full table for all possible values that $X + Y$ can take
  - There may be a lot!
  - Then work out expectation from the table
- Or use the formula $E (X + Y) = E (X) + E (Y)$
  - Find $E (X)$ and $E (Y)$ from their tables above
Note that, if $X$ and $Y$ are independent
- Then $E (X Y) = E (X) E (Y)$
- The expectation of a product is the product of the expectation
These ideas can be applied when repeatedly using the same distribution, $X$
- For example, flipping a coin, then flipping it again
- Create independent random variables $X_{1}, X_{2}, . . .$

What if they introduce a new dependent variable?

Sometimes questions introduce a new variable, $Y$ , which depends on an old variable, $X$
$x$
-3
1
2
3
$P (X = x)$
0.25
0.25
0.25
0.25
- Let $Y = 9 - X^{2}$
  - List values of $y$
  - They have the same probabilities as $X$ (as $Y$ depends on $X$ )
  - $y$
    0
    8
    5
    0
    $P (Y = y)$
    0.25
    0.25
    0.25
    0.25
    Simplify (reorder and group values together)
  $y$
  0
  5
  8
  $P (Y = y)$
  0.5
  0.25
  0.25
You can use $E (X + Y) = E (X) + E (Y)$
- calculate $E (X)$ and $E (Y)$ from their tables
You cannot use $E (X Y) = E (X) E (Y)$ if $Y$ depends on $X$
- To find $E (X Y)$ draw the table for all possible values of $X Y$
  $x y$
  -3 × 0
  1 × 8
  2 × 5
  3 × 0
  $P (X = x)$
  0.25
  0.25
  0.25
  0.25
  - Probabilities are the same as $X$ (as $Y$ depends on $X$ )
  - Then calculate expectation from this table
- Alternatively, substitute in $Y$
  - $X Y = X (9 - X^{2}) = 9 X - X^{3}$
  - So $E (9 X - X^{3}) = 9 E (X) - E (X^{3})$
  - Find $E (X)$ from the table of $X$
  - Find $E (X^{3})$ from the table of $X$ (by cubing the $x$ values)

What if there is conditional probability?

Learn the conditional probability formula
- $P (A | B) = \frac{P (A \cap B)}{P (B)}$
- For example, for integer values, the probability that $X > 5$ given that $X \leq 10$
  - $P (X > 5 | X \leq 10) = \frac{P (6 \leq X \leq 10)}{P (X \leq 10)}$

Examiner Tips and Tricks

Always draw out tables of values for each DRV – they really help in the exam!

Worked Example

In a game, you can earn 2, 5 or 6 points. There is a 50% chance of earning 6 points and an equal chance of earning either 2 or 5 points.

a) Find the probability of earning more than 9 points when playing the game twice.

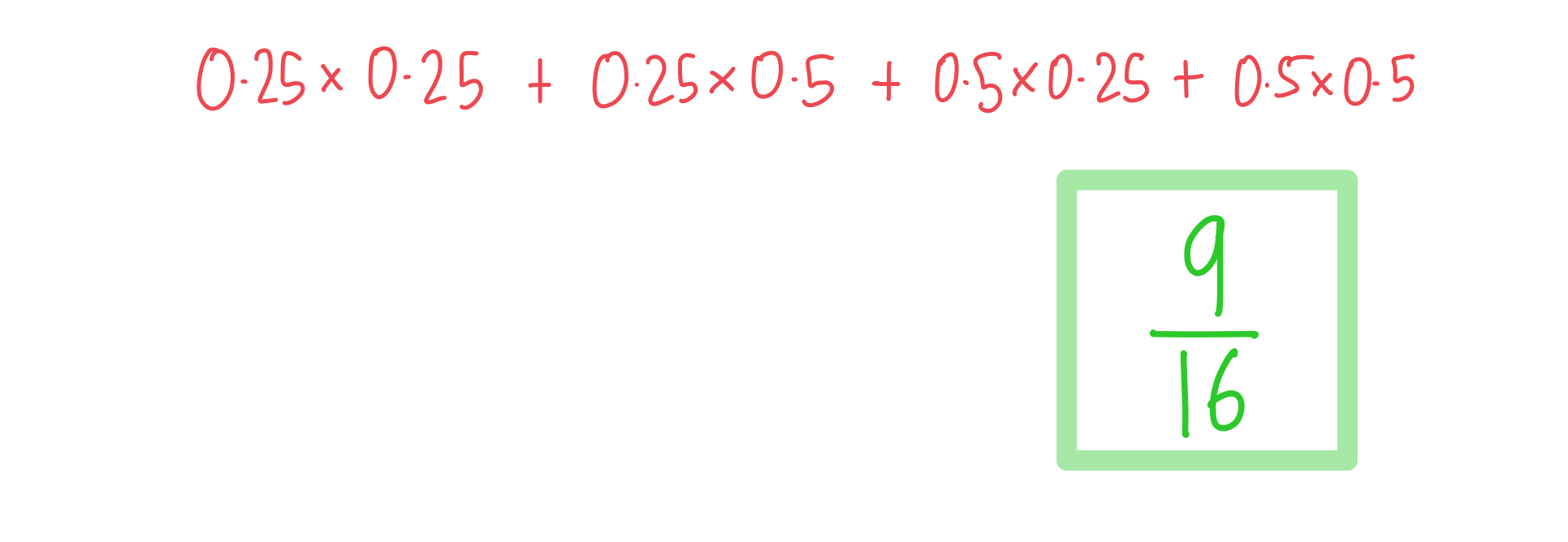
The amount of money (£) won in a game is found by multiplying the number of points, $X$ , by the variable $Y$ , where $Y = 3$ if $X < 5$ or $Y = X - 3$ if $X \geq 5$ .

b) Find the expected amount of money won per game.

Further Maths: Further Statistics 1