oblique-collisions-of-two-spheres

Oblique collisions of two spheres

What is an oblique collision between two spheres?

• An oblique collision between two spheres is when two spheres which are not travelling along the same straight line collide

  • For the purposes of this course, the spheres are modelled as smooth, and as having equal radii

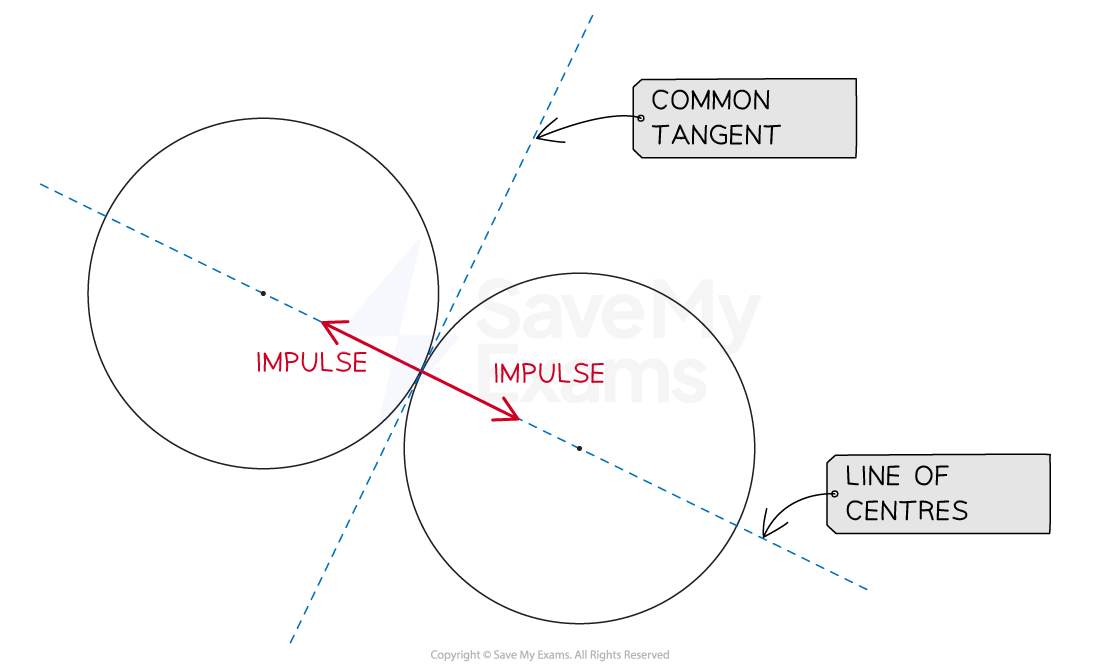
• When they collide, they touch at a single point, and so share a common tangent

• Perpendicular to the common tangent, is the line of centres, which passes through the centre of both spheres

• Similar to when colliding with a surface, the objects only meet at a single point,

  • so the impulse only acts perpendicular to the ‘surface’,

    • in this case the ‘surface’ is another sphere

• Therefore the impulse acts along the line of centres

How do I solve problems involving oblique collisions between two spheres?

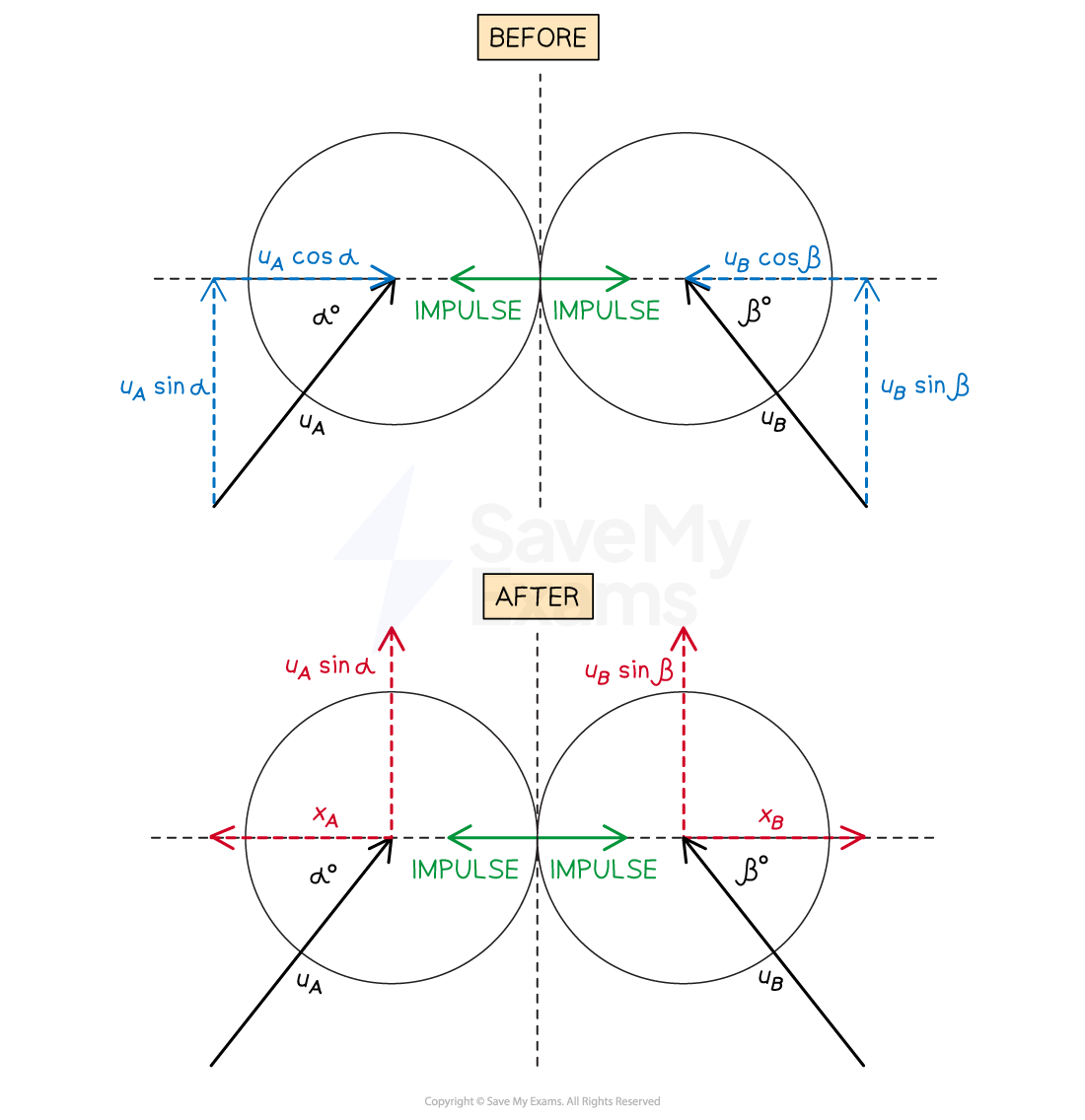
The diagram below shows how to model the collision of spheres A and B, moving with speeds and  at angles  and  respectively to the line of centres. (Note that the line of centres has been drawn horizontally in this diagram, but all the expressions shown will be exactly the same whatever the direction of the line of centres is.) 

• As the impulse only acts along the line of centres, it is only this component of the velocity which will be affected

  • In the diagram it can be seen that for the components parallel to the line of centres:

    • becomes ; the ‘line of centres’ component of A after the collision

    • becomes ; the ‘line of centres’ component of B after the collision

    • and  can be calculated later

• The component of the velocity perpendicular to this, which is in the direction of the common tangent, is unaffected by the collision

  • In the diagram it