newtons-law-of-restitution

Newton’s law of restitution

What is Newton’s law of restitution?

• Newton’s law of restitution (also known as Newton’s experimental law) concerns the ratio of the relative speed of separation and the relative speed of approach when two objects collide

  • Essentially this just means the speed of separation divided by the speed of approach

• This ratio can be written as a coefficient; the “coefficient of restitution”

  • It is denoted by e

  • e is dimensionless as it is a ratio

  • The value of e in a particular situation will depend on the materials that the two particles are made from

• e can take the values in the range 0 ≤ e ≤ 1

  • e =1: These are called perfectly elastic collisions and in these collisions there is no loss in kinetic energy

  • e =0: These are called perfectly inelastic collisions and in these collisions the objects coalesce (merge to form one object)

How do I calculate the coefficient of restitution between two objects?

• 

• The speed of approach depends on whether the objects are travelling towards each other or in the same direction. For example, if the speeds of the two objects before the collision are 5 m s^-1 and 2 m s^-1 then the speed of approach is:

  • 3 m s^-1 if they are moving in the same direction (each second the objects approach each other by a further 3 metres)

  • 7 m s^-1 if they are moving in opposite directions (each second the objects approach each other by a further 7 metres)

• The speed of separation depends on whether the objects are travelling away from each other or in the same direction. For example, if the speeds of the two objects after the collision are 5 m s^-1 and 2 m s^-1 then the speed of separation is:

  • 3 m s^-1 if they are moving in the same direction (each second the objects separate by a further 3 metres)

  • 7 m s^-1 if they are moving in opposite directions (each second the objects separate by a further 7 metres)

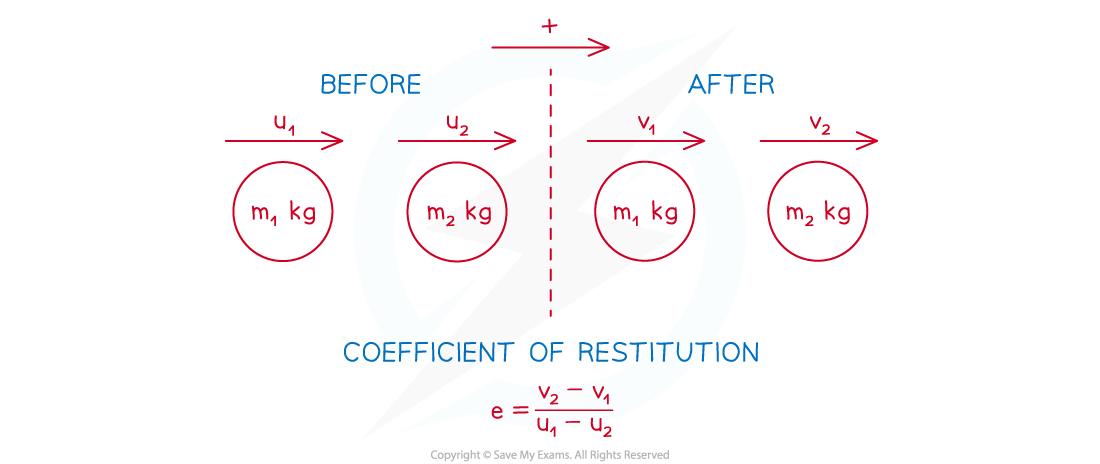
• If the velocities of the two objects before the collision are u₁ m s^-1 and u₂ m s^-1 and the velocities after the collision are v₁m s^-1 and v₂ m s^-1 then:

  •  

  • Note that velocities can be negative so be careful with signs

How do I solve collision problems involving the coefficient of restitution?

• STEP 1: Draw a before/after diagram and label the positive direction

  • There may be multiple diagrams if there are multiple collisions

• STEP 2: Form an equation using the coefficient of restitution

  • The unknown(s) could be the coefficient of restitution or any of the speeds or directions

• STEP 3: Form an equation using the principle of conservation of momentum

  • In the case of a collision with a wall you may be given the impulse or some other information instead

• STEP 4: Solve and give your answer in context

  • You may have to solve simultaneous equations

  • You may have to solve an inequality

  • You may have to form an inequality using 0 ≤ e ≤ 1 or using the fact that velocity is positive (or negative) if the object is going forwards (or backwards)