shortest-distances—planes

课 Progress

0% Complete

Shortest distance between a point & a plane

How do I find the shortest distance between a given point on a line and a plane?

The shortest distance from any point on a line to a plane will always be the perpendicular distance from the point to the plane
Given a point, P, on the line $l$ with equation $bold r equals bold a plus lambda bold b$ and a plane $capital pi$ with equation $begin mathsize 16px style bold r times bold n equals d end style$
- STEP 1: Find the vector equation of the line perpendicular to the plane that goes through the point, P, on $size 16px l$
  - This will have the position vector of the point, P, and the direction vector n
- STEP 2: Find the coordinates of the point of intersection of this new line with $capital pi$ by substituting the equation of the line into the equation of the plane
- STEP 3: Find the distance between the given point on the line and the point of intersection
  - This will be the shortest distance from the plane to the point
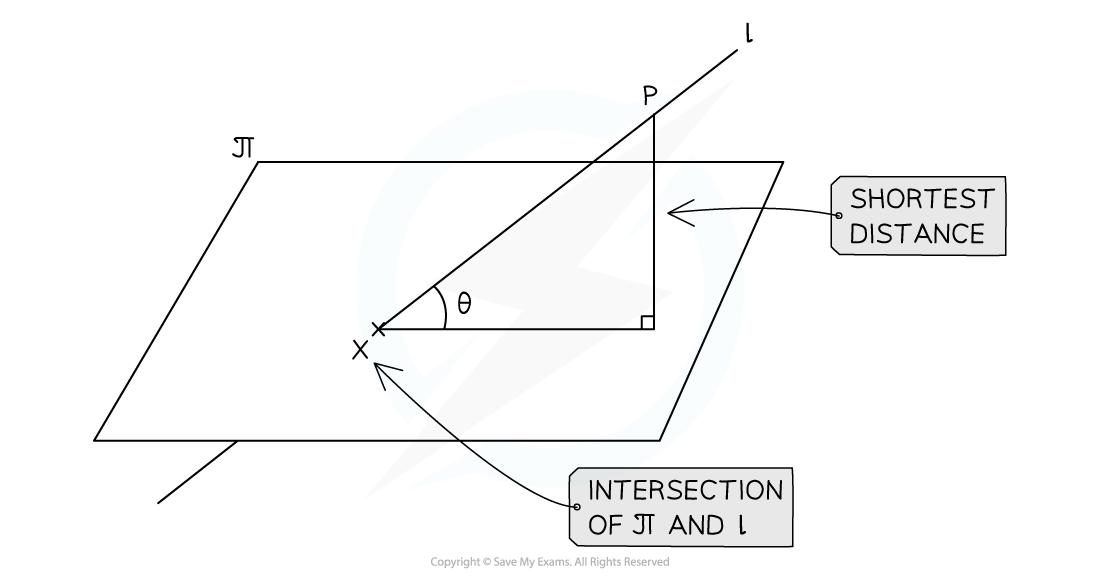
A question may provide the acute angle between the line and the plane
- Use right-angled trigonometry to find the perpendicular distance between the point on the line and the plane
  - Drawing a clear diagram will help

ZAFnkWOW_3-11-4-ib-hl-aa-shortest-dist-two-planes-diagram-1

Worked Example

The plane $capital pi$ has equation <img alt=”bold r times open parentheses table row 2 row cell negative 1 end cell row 1 end table close parentheses equals 6″ data-mathml='<math ><semantics><mstyle mathsize=”16px”><mi mathvariant=”bold”>r</mi><mo>⋅</mo><mfenced separators=”|”><mtable><mtr><mtd><mn>2</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>1</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable></mfenced><mo>=</mo><mn>6</mn></mstyle><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″}</annotation></semantics></math>’ height=”69″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2269%22%20width%3D%2283%22%20wrs%3Abaseline%3D%2240%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmstyle%20mathsize%3D%2216px%22%3E%3Cmi%20mathvariant%3D%22bold%22%3Er%3C%2Fmi%3E%3Cmo%3E%26%23x22C5%3B%3C%2Fmo%3E%3Cmfenced%20separators%3D%22%7C%22%3E%3Cmtable%3E%3Cmtr%3E%3Cmtd%3E%3Cmn%3E2%3C%2Fmn%3E%3C%2Fmtd%3E%3C%2Fmtr%3E%3Cmtr%3E%3Cmtd%3E%3Cmo%3E-%3C%2Fmo%3E%3Cmn%3E1%3C%2Fmn%3E%3C%2Fmtd%3E%3C%2Fmtr%3E%3Cmtr%3E%3Cmtd%3E%3Cmn%3E1%3C%2Fmn%3E%3C%2Fmtd%3E%3C%2Fmtr%3E%3C%2Fmtable%3E%3C%2Fmfenced%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmn%3E6%3C%2Fmn%3E%3C%2Fmstyle%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math135b31cfba37a56451b4768509d’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAAA%2FGhlYWQQC2qxAAACkAAAADZoaGVhCGsXSAAAAsgAAAAkaG10eE2rRkcAAALsAAAADGxvY2EAHTwYAAAC%2BAAAABBtYXhwBT0FPgAAAwgAAAAgbmFtZaBxlY4AAAMoAAABn3Bvc3QB9wD6AAAEyAAAACBwcmVwa1uragAABOgAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0iEv%2F%2FAAAAPSIS%2F%2F%2F%2FxN3wAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAEAgAFVAtUBqwADADAYAbAEELEAA%2FawAzyxAgf1sAE8sQUD5gCxAAATELEABuWxAAETELABPLEDBfWwAjwTIRUhgAJV%2FasBq1YAAQAAAAEAANV4zkFfDzz1AAMEAP%2F%2F%2F%2F%2FWOhNz%2F%2F%2F%2F%2F9Y6E3MAAP8gBIADqwAAAAoAAgABAAAAAAABAAAD6P9qAAAXcAAA%2F7YEgAABAAAAAAAAAAAAAAAAAAAAAwNSAFUDVgCAA1YAgAAAAAAAAAAoAAAAsgAAAPwAAQAAAAMAXgAFAAAAAAACAIAEAAAAAAAEAADeAAAAAAAAABUBAgAAAAAAAAABABIAAAAAAAAAAAACAA4AEgAAAAAAAAADADAAIAAAAAAAAAAEABIAUAAAAAAAAAAFABYAYgAAAAAAAAAGAAkAeAAAAAAAAAAIABwAgQABAAAAAAABABIAAAABAAAAAAACAA4AEgABAAAAAAADADAAIAABAAAAAAAEABIAUAABAAAAAAAFABYAYgABAAAAAAAGAAkAeAABAAAAAAAIABwAgQADAAEECQABABIAAAADAAEECQACAA4AEgADAAEECQADADAAIAADAAEECQAEABIAUAADAAEECQAFABYAYgADAAEECQAGAAkAeAADAAEECQAIABwAgQBNAGEAdABoACAARgBvAG4AdABSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAE0AYQB0AGgAIABGAG8AbgB0AE0AYQB0AGgAIABGAG8AbgB0AFYAZQByAHMAaQBvAG4AIAAxAC4AME1hdGhfRm9udABNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAMAAAAAAAAB9AD6AAAAAAAAAAAAAAAAAAAAAAAAAAC5BxEAAI2FGACyAAAAFRQTsQABPw%3D%3D)format(‘truetype’)%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A’brack_sm2882ad605b1e27be87c7468’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7PH4UAAADMAAAATmNtYXA3kjw6AAABHAAAADxjdnQgAQYDiAAAAVgAAAASZ2x5ZkyYQ7YAAAFsAAAAkWhlYWQLyR8fAAACAAAAADZoaGVhAq0XCAAAAjgAAAAkaG10eDEjA%2FUAAAJcAAAADGxvY2EAAEKZAAACaAAAABBtYXhwBJsEcQAAAngAAAAgbmFtZW7QvZAAAAKYAAAB5XBvc3QArQBVAAAEgAAAACBwcmVwu5WEAAAABKAAAAAHAAACDAGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg9AMD%2FP%2F8AAABVAABAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACI5wjn%2F%2F%2FAAAjnCOf%2F%2F%2FcZdxjAAEAAAAAAAAAAAFUAFQBAAArAIwAgACoAAcAAAACAAAAAADVAQEAAwAHAAAxMxEjFyM1M9XVq4CAAQHWqwABAAAAAABVAVgAAwAfGAGwAy%2BwADyxAgL1sAE8ALEDAD%2BwAjx8sQAG9bABPBEzESNVVQFY%2FqgAAQDXAAABLAFUAAMAIBgBsAUvsAE8sAI8sQAC9bADPACwAy%2BwAjyxAAH1sAE8EzMRI9dVVQFU%2FqwAAAAAAQAAAAEAAIsesexfDzz1AAMEAP%2F%2F%2F%2F%2FVre5k%2F%2F%2F%2F%2F9Wt7mT%2FgP%2F%2FAdYBWAAAAAoAAgABAAAAAAABAAABVP%2F%2FAAAXcP%2BA%2F4AB1gABAAAAAAAAAAAAAAAAAAAAAwDVAAABLAAAASwA1wAAAAAAAAAhAAAAWAAAAJEAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABlAAAAAAAAABUBAgAAAAAAAAABACYAAAAAAAAAAAACAA4AJgAAAAAAAAADAEQANAAAAAAAAAAEACYAeAAAAAAAAAAFABYAngAAAAAAAAAGABMAtAAAAAAAAAAIABwAxwABAAAAAAABACYAAAABAAAAAAACAA4AJgABAAAAAAADAEQANAABAAAAAAAEACYAeAABAAAAAAAFABYAngABAAAAAAAGABMAtAABAAAAAAAIABwAxwADAAEECQABACYAAAADAAEECQACAA4AJgADAAEECQADAEQANAADAAEECQAEACYAeAADAAEECQAFABYAngADAAEECQAGABMAtAADAAEECQAIABwAxwBCAHIAYQBjAGsAZQB0AHMAIABzAG0AYQBsAGwAIABzAGkAegBlAFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAQgByAGEAYwBrAGUAdABzACAAcwBtAGEAbABsACAAcwBpAHoAZQBCAHIAYQBjAGsAZQB0AHMAIABzAG0AYQBsAGwAIABzAGkAegBlAFYAZQByAHMAaQBvAG4AIAAyAC4AMEJyYWNrZXRzX3NtYWxsX3NpemUATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAAAqgBVAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAo2FAA%3D%3D)format(‘truetype’)%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A’stixf4d87ed3b0dbf9c79746d00cedb’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAANAIAAAwBQT1MvMi8nBU0AAADcAAAATmNtYXDCjdaBAAABLAAAADRjdnQgSG4BcAAAAWAAAADYZnBnbUUgjnwAAAI4AAANbWdseWYcKO%2BSAAAPqAAAADtoZWFkDLPdGwAAD%2BQAAAA2aGhlYQjYEyQAABAcAAAAJGhtdHg0LeORAAAQQAAAAAhsb2NhTQ9wLwAAEEgAAAAMbWF4cBlhFX0AABBUAAAAIG5hbWV4T00CAAAQdAAAAZ5wb3N0AgIA%2FwAAEhQAAAAgcHJlcFWzoI8AABI0AAAAvAAAApwBkAAFAAAD6APoAAAAAAPoA%2BgAAAAAAAEA%2BgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAgICAgAAAAINf%2FAqX%2BvQAAA%2F8B5gAAAAAAAgABAAEAAAAUAAMAAQAAABQABAAgAAAABAAEAAEAACLF%2F%2F8AACLF%2F%2F%2FdPAABAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFoAWgAcABwClgAAAcIAAP8nA%2F%2F%2BGgKk%2F%2FIBzP%2F2%2FyYD%2F%2F4aAFkAWQAgACAClgAAAqsBwv%2F2%2FycD%2F%2F4aAqT%2F8gKrAcz%2F9v8mA%2F%2F%2BGgBaAFoAHAAcApYAAAKrAcIAAP8nA%2F%2F%2BGgKk%2F%2FICqw

Further Maths: Core Pure -Edexcel-A Level

shortest-distances—planes

Shortest distance between a point & a plane

How do I find the shortest distance between a given point on a line and a plane?

Worked Example

Responses