intro-to-differential-equations

General solutions

What is a differential equation?

• Any equation, involving a derivative term, is a differential equation

• Equations involving only first derivative terms are called first order differential equations

• Equations involving second derivative terms are called second order differential equations

What is a general solution?

• Integration will be involved in solving the differential equation

  • ie working back to “y = f(x)”

• A constant of integration, c is produced

• This gives an infinite number of solutions to the differential equation, each of the form y = g(x) + c (ie y = f(x) where f(x) = g(x) + c)

• … and the solution y= g(x) + c is called the general solutionThese are often called a family of solutions …

Particular solutions

What is a particular solution?

• Ensure you are familiar with General Solutions first

• With extra information, the constant of integration, c, can be found

• This means the particular solution (from the family of solutions) can be found

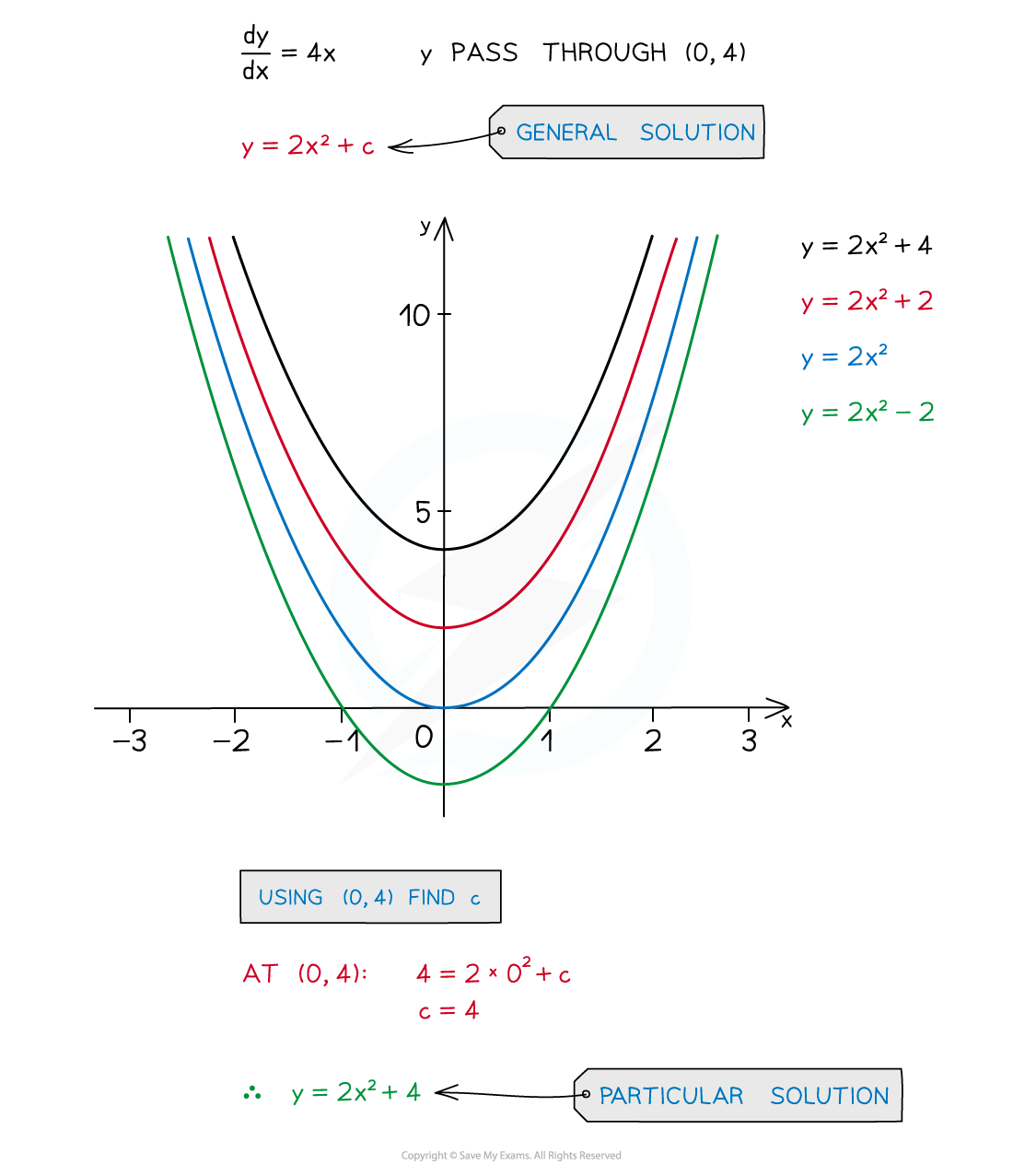
What is a boundary condition/initial condition?

A boundary condition is a piece of extra information that lets you find the particular solution

• For example knowing y = 4 when x = 0 in the preceding example

• In a model this could be a particle coming to rest after a certain time, ie v = 0 at time t

• Differential equations are used in modelling, experiments and real-life situations

• A boundary condition is often called an initial condition when it gives the situation at the start of the model or experiment

• This is often linked to time, so t = 0

• It is possible to have two boundary conditions

  • eg a particle initially at rest has velocity, v = 0 and acceleration, a = 0 at time, t = 0

  • for a second order differential equation you need two boundary conditions to find the particular solution