linear-search

Linear search

What is a linear search?

• The linear search is a standard algorithm used to find elements in an unordered list

• The list is searched sequentially and systematically from the start to the end one element at a time

• Comparing each element to the value being searched for

  • If the value is found the algorithm outputs where it was found in the list

  • If the value is not found it outputs a message stating it is not in the list

• An example of using a linear search would be looking for a specific student name in a list or searching for a supermarket item in a shopping list

Performing the linear search

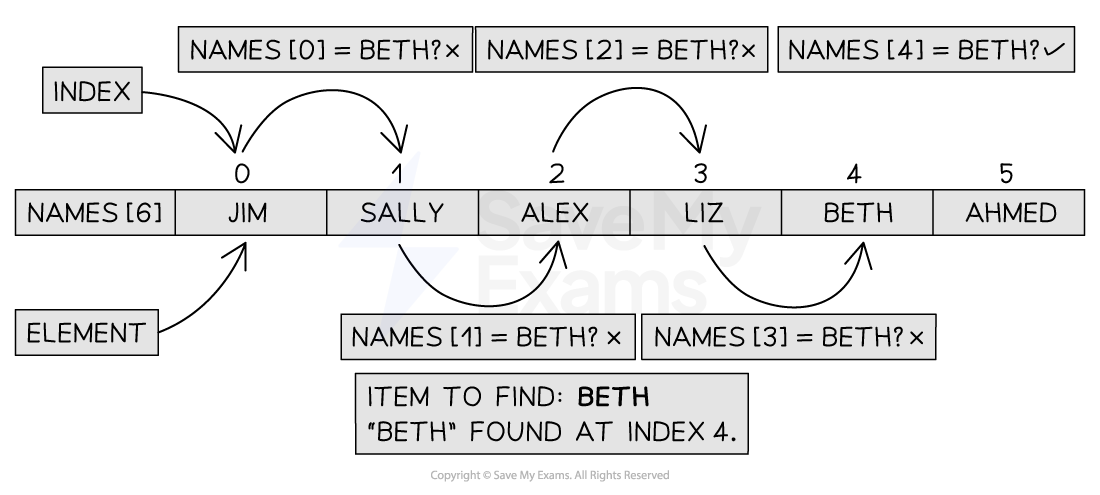
Figure 1: Performing the Linear Search

Time complexity of a linear search

• To determine the algorithm’s execution time as measured by the number of instructions or steps carried out, Big-O notation must be used

• The loop is executed n times, once for each item. There are two instructions within the loop, the if statement and an assignment, hence the Big-O for the loop is O(2n)

• There are three initial statements which are O(1)

• The overall Big-O notation is therefore 2n + 3, which when coefficients are factored out, becomes O(n) as linear time dominates constant time. The constant term and coefficients contribute significantly less as the input size n grows larger

• It is important to remember here that O(n) is the worst case scenario. The best case scenario O(1) would find the item the first time, while the average case would be O(n/2) which when we remove coefficients still becomes O(n)

Space complexity of a linear search

• As the linear search requires no additional space, it is space complexity O(n) where n is the number of items in the list

Tracing a linear search

• Given the following list [5, 4, 7, 1, 3, 8, 9, 2], a trace table for the linear search is shown below

Trace Table of the Linear Search

Implementing a linear search

Pseudocode

FUNCTION linearSearch(list : ARRAY OF STRING, item : STRING) RETURNS INTEGER DECLARE index : INTEGER DECLARE i : INTEGER DECLARE found : BOOLEAN index ← -1 i ← 0 found ← FALSE WHILE i < LENGTH(list) AND found = FALSE IF list[i] = item THEN index ← i found ← TRUE ENDIF i ← i + 1 ENDWHILE RETURN index
ENDFUNCTION

• Function definition:
  FUNCTION linearSearch(list : ARRAY OF STRING, item : STRING) RETURNS INTEGER

  • The function takes a list and a target item.

  • It returns the index of the item if found, or -1 if not.

• Variable declarations:
  index, i, and found are declared:

  • index stores the result (default is -1 if not found).

  • i is the loop counter.

  • found is a boolean used to stop the search once the item is found.

• Initialisation:

  • index ← -1 → start with “not found”

  • i ← 0 → start from the first index of the list

  • found ← FALSE → the item hasn’t been found yet

• Loop condition:
  WHILE i < LENGTH(list) AND found = FALSE

  • Continue looping while there are items left to check and the item hasn’t been found.

• Comparison inside loop:
  IF list[i] = item THEN

  • Check if the current element equals the search item.

• If a match is found:

  • index ← i → save the current index

  • found ← TRUE → stop searching

• Increment:

  • i ← i + 1 → move to the next item

• End of loop:

  • Once the loop finishes (either item is found or end of list is reached), return the result.

• Return value:
  RETURN index

  • Returns the index where the item was found.

  • If it wasn’t found, it returns -1.

Python

def linear_search(list, item): index = -1 for i in range(len(list)): if list[i] == item: index = i break # Stop the loop once the item is found return index

Java

public class LinearSearch { public static int linearSearch(int[] list, int item) { int index = -1; for (int i = 0; i < list.length; i++) { if (list[i] == item) { index = i; break; // Stop the loop once the item is found } } return index; }