Computer-science_A-level_Cie
-
computers-and-components6 主题
-
logic-gates-and-logic-circuits2 主题
-
central-processing-unit-cpu-architecture6 主题
-
assembly-language-4 主题
-
bit-manipulation1 主题
-
operating-systems3 主题
-
language-translators2 主题
-
data-security3 主题
-
data-integrity1 主题
-
ethics-and-ownership3 主题
-
database-concepts3 主题
-
database-management-systems-dbms-1 主题
-
data-definition-language-ddl-and-data-manipulation-language-dml1 主题
-
computational-thinking-skills1 主题
-
algorithms14 主题
-
data-types-and-records2 主题
-
arrays2 主题
-
files1 主题
-
introduction-to-abstract-data-types-adt1 主题
-
programming-basics1 主题
-
constructs2 主题
-
structured-programming1 主题
-
program-development-life-cycle2 主题
-
program-design-2 主题
-
program-testing-and-maintenance3 主题
-
user-defined-data-types1 主题
-
file-organisation-and-access-3 主题
-
floating-point-numbers-representation-and-manipulation3 主题
-
protocols2 主题
-
circuit-switching-packet-switching1 主题
-
processors-parallel-processing-and-virtual-machines5 主题
-
boolean-algebra-and-logic-circuits4 主题
-
purposes-of-an-operating-system-os3 主题
-
translation-software3 主题
-
encryption-encryption-protocols-and-digital-certificates3 主题
-
artificial-intelligence-ai4 主题
-
recursion1 主题
-
programming-paradigms4 主题
-
object-oriented-programming7 主题
-
file-processing-and-exception-handling2 主题
-
data-representation5 主题
-
multimedia3 主题
-
compression2 主题
-
networks-and-the-internet11 主题
binary-search
Binary search
What is a binary search?
-
The binary search is a more efficient search method than linear search
-
The binary search compares the middle item to the searched for target item. If the values match then the index is returned. If not then the list is adjusted such that:
-
the top half is ignored if the target item is less than the middle value
-
or the bottom half is ignored if the target item is larger than the middle value
-
-
Once the list has been adjusted, the search continues until the item is found or the item is not in the list
-
It is important to note that the list must be sorted for the binary search to work correctly
-
The implementation of the binary search is shown below
Performing the binary search
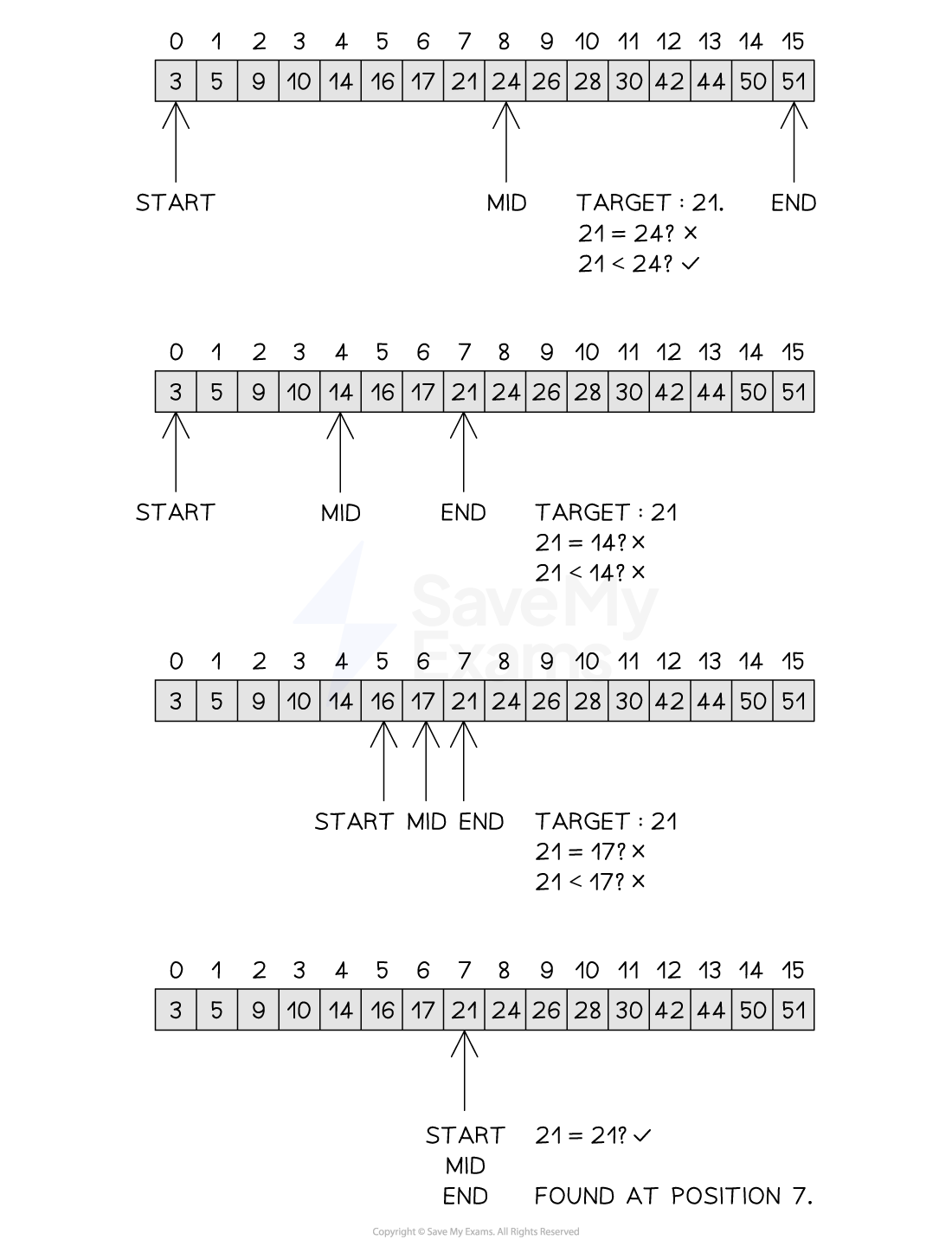
Figure 2: Performing the Binary Search
Examiner Tips and Tricks
-
When determining the rounding of the midpoint, rounding up or down are both valid provided consistent use of the same rounding is used throughout the algorithm
-
It is important to note that the binary search does not discard, delete or remove parts of the list, it only adjusts the start, end and mid pointers. This only gives the appearance that items have been discarded or deleted
Time complexity of a binary search
-
The binary search is an example of a logarithmic time complexity O(logn) as it halves the search space with each iteration of the while loop. This approach is known as divide and conquer, where a problem is progressively reduced in size such that when each problem is at its smallest it is easiest to solve
-
The algorithm starts with n items before the first iteration. After the first there are n/2 items, after the second there are n/4 items, after the third there are n/8 items and so on, leading to n/2i after i iterations
-
The worst case scenario or maximum number of iterations to find one item is where n/2i = 1
-
Multiply both sides by 2i to get: n = 2i
-
Take the logarithm of both sides: logn = log2i
-
Rewrite with i at the front (using laws of logarithms): logn = ilog2
-
Log2 (assuming a base of 2 is used) becomes 1, giving: logn = i
-
The binary search is therefore O(logn)
-
-
The best case scenario would be O(1) where the item is found on the first comparison, while the average case would be O(logn/2) which would find the item somewhere in the middle of the search. Removing coefficients means the average case would therefore still be O(logn)
Space complexity of a binary search
-
As the binary search requires no additional space, it is space complexity O(n), where n is the number of items in the list
Tracing a binary search
-
Given the following list [3, 5, 9, 10, 14, 16, 17, 21, 24, 26, 28, 30, 42, 44, 50, 51], a trace table for the binary search is shown below
Trace Table for the Binary Search
|
item |
index |
found |
start |
end |
mid |
list[mid] |
|---|---|---|---|---|---|---|
|
21 |
-1 |
False |
0 |
15 |
8 |
24 |
|
|
|
|
0 |
7 |
4 |
14 |
|
|
|
|
5 |
7 |
6 |
17 |
|
21 |
7 |
True |
7 |
7 |
7 |
21 |
Implementing a binary search
Pseudocode
FUNCTION binarySearch(list : ARRAY OF INTEGER, item : INTEGER) RETURNS INTEGER DECLARE found : BOOLEAN DECLARE index : INTEGER DECLARE start : INTEGER DECLARE end : INTEGER DECLARE mid : INTEGER found ← FALSE index ← -1 start ← 0 end ← LENGTH(list) - 1 WHILE start <= end AND found = FALSE mid ← (start + end) DIV 2 IF list[mid] = item THEN found ← TRUE index ← mid ELSE IF list[mid] < item THEN start ← mid + 1 ELSE end ← mid - 1 ENDIF ENDIF ENDWHILE RETURN index
ENDFUNCTION-
Function definition:
FUNCTION binarySearch(list : ARRAY OF INTEGER, item : INTEGER) RETURNS INTEGER-
The function searches a sorted array for a given item.
-
It returns the index of the item if found, or -1 if not found.
-
-
Variable declarations:
-
found→ a flag to indicate if the item is found (initiallyFALSE) -
index→ the result to be returned (initially-1) -
start→ index of the start of the current search range (initially0) -
end→ index of the end of the current search range (initiallyLENGTH(list) - 1) -
mid→ index of the middle element in the current range
-
-
Loop condition:
WHILE start <= end AND found = FALSE-
Keep searching while the search range is valid and the item hasn’t been found.
-
-
Middle element calculation:
mid ← (start + end) DIV 2-
Calculates the index of the middle element of the current search range.
-
-
Check for match:
IF list[mid] = item THEN-
If the middle element is equal to the target item:
-
Set
found ← TRUE -
Store the
index ← mid
-
-
-
Adjust search range:
-
If the middle value is less than the item:
-
Search the right half →
start ← mid + 1
-
-
Otherwise:
-
Search the left half →
end ← mid - 1
-
-
-
Loop ends:
-
The loop stops when the item is found or the search range becomes invalid.
-
-
Return value:
RETURN index-
Returns the index if found, or
-1if not found
-
Python
def binary_search(list, item): found = False index = -1 start = 0 end = len(list) - 1 while start <= end and not found: mid = (start + end) // 2 if list[mid] == item: found = True index = mid elif list[mid] < item: start = mid + 1 else: end = mid - 1 return indexJava
public class BinarySearch { public static int binarySearch(int[] list, int item) { boolean found = false; int index = -1; int start = 0; int end = list.length - 1; while (start <= end && !found) { // Corrected found condition int mid = (start + end) / 2; if (list[mid] == item) { found = true; index = mid; } else if (list[mid] < item) { start = mid + 1; } else { end = mid - 1; } } return index; }
Responses