hash-tables

Hash Tables

What is a hash table?

• In A Level Computer Science, a hash table is an associative array which is coupled with a hash function

• The function takes in data and releases an output

• The role of the hash function is to map the key to an index in the hash table. 

• Each piece of data is mapped to a unique value using the hash function

• It is sometimes possible for two inputs to result in the same hashed value. This is known as a collision

• A good hashing algorithm should have a low probability of collisions occurring but if it does occur, the item is typically placed in the next available location. This is called collision resolution

• Hash tables are normally used for indexing as they provide fast access to data due to keys having a unique 1-1 relationship with the address at which they are stored. 

• Hash tables enable very efficient searching. In the best case, data can be retrieved from a hash table in constant time 

Character hash table

• Not all key values are simple integers so if it’s a character then the hash function will need to do more processing. 

• An alphanumeric key that is made up of any four letters or numbers. An example would be C6IA

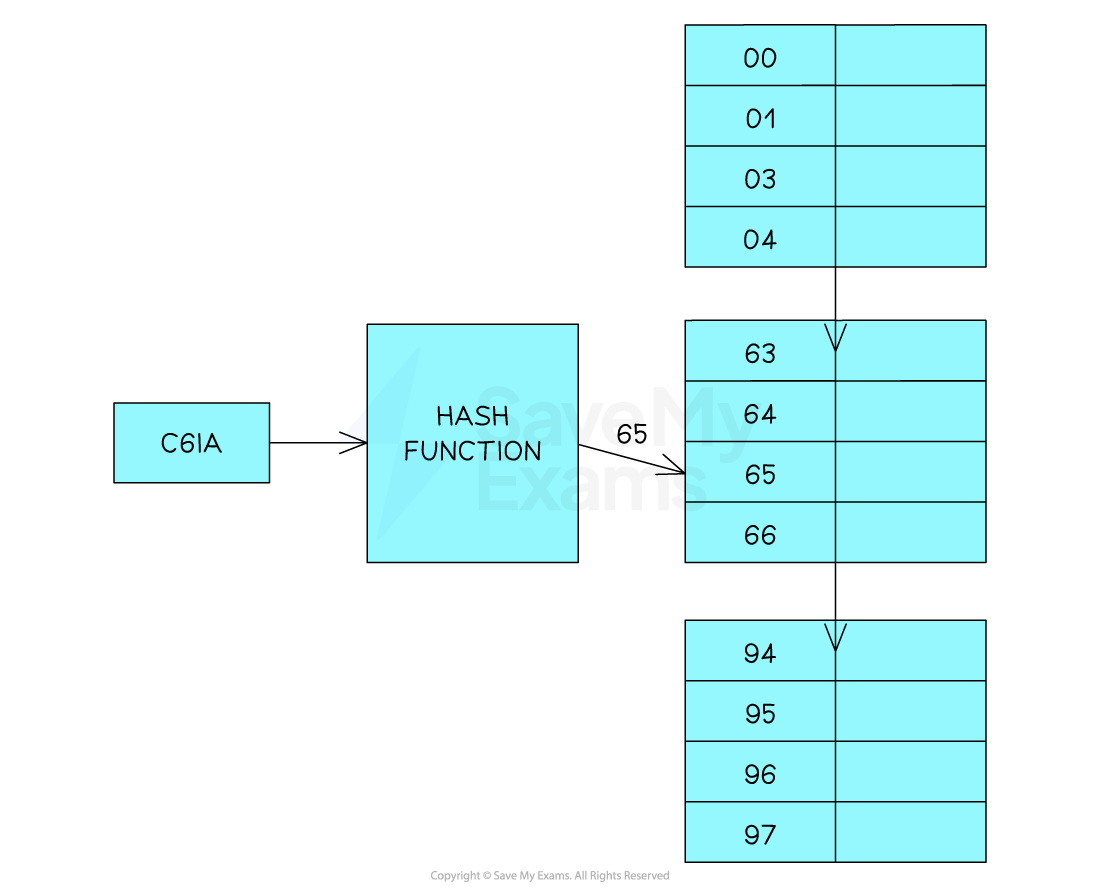
• To hash the code, the characters can be converted to their ASCII value codes:

• Then add the values to get a total: 67 + 54 + 73 + 65 = 259

• Then we apply the MOD function: 259 MOD 97 = 65

• This then means the data associated with C6IA will be stored in position 65 in the hash table

Collisions in a hash table

• A collision occurs when the hash function produces the same hash value for two or more keys

• B7MF produces the same hash value (74) as A5RD

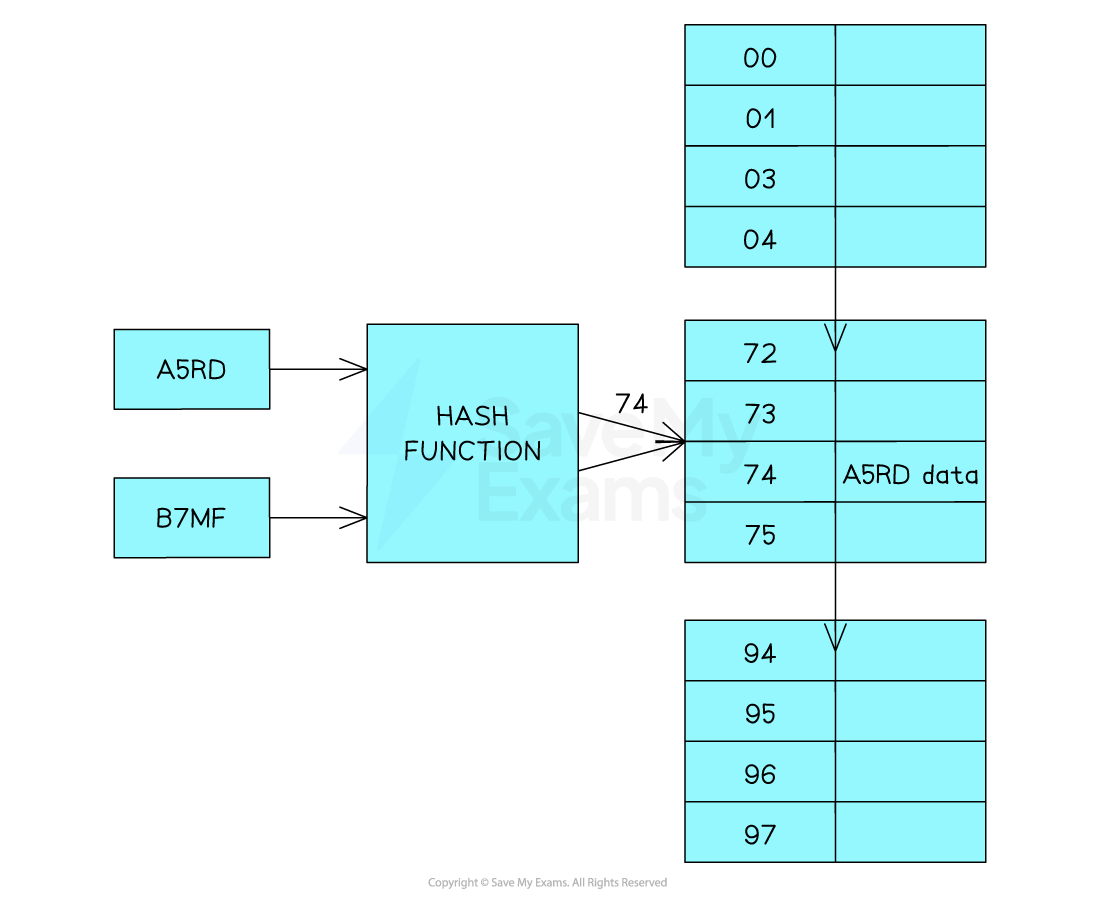
• Collisions are a problem when using hash tables because you can’t store two sets of data at the same location.

• There are two ways to handle collisions Linear probing or chaining

Linear probing

• When there is a collision the data is placed in the next free position in the hash table

• Either it can probe sequentially or use an interval (e.g check every 3rd slot) until an empty bucket is found

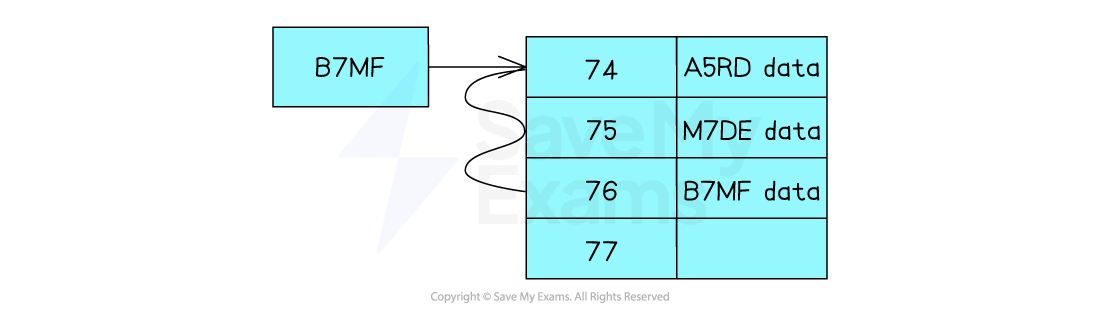
• In the diagram the data with the key A5RD has already been inserted into the location 74 of the table. When you want to insert B7MF the same hash value is produced

• So because the space is already occupied by A5RD it checks the next location which is 75, as this is occupied it checks the next location which is 76 which is empty so the data will be placed in this location

• If there are lots of collisions the hash table can end up very messy

Retrieving Data:

• When there has been a collision the data will not be in the correct location. The process of retrieving data from the table where collisions have been dealt with by linear probing is as follows:

  • Hash the key to generate the index value

  • Examine the indexed position to see if the key (which is stored together with the data) matches the key of the data you are looking for

  • If there is no match then each location that follows is checked (at the appropriate interval) until the matching record is found

  • If you reach an empty bucket without finding a matching key then the data is not in the hash table

• This significantly reduces the efficiency of using a hash table for searching. 

• Hash tables should always be designed to have extra capacity

Chaining

• Another way of dealing with collisions is to use linked lists. Instead of storing the actual data in the hash table, you store a pointer to a location where the data is stored. Each data item is stored as a node with 3 attributes:

  • The key value

  • The data

  • A pointer to the next node

• The first value to be stored will have a Null pointer as it is the only item in the list

• When there is a collision the pointer for the first node location will be updated to point to the new node

• This will create a chain of nodes whose keys resolve to the same hash value

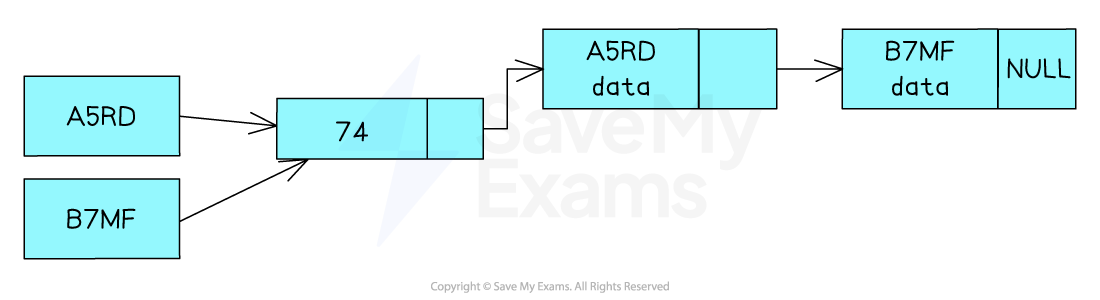
Retrieving data

• When collisions have been dealt with using chaining the data will always be accessed through a single location in the hash table. The process for retrieving it is as follows:

  • Hash the key to generate the index value

  • Examine the key of the node to see if it matches the key that you are looking for

  • If it is not the node you are looking for follow the linked list until you find the node

  • If you reach the end of the list without finding a matching key (or the head pointer was null), the data is not in the hash table

• In the worse case (where every key hashes to the same value), you could still end up carrying out a linear search 

• It is important that the hash function is designed and tested to minimise the number of possible collisions

Rehashing

• Items will be added and deleted from the hash table. If the table starts to fill up, or a large number of items are in the wrong place, the performance of the hash table will degrade. Rehashing is used to address this problem

• Rehashing created a new table (larger if needed). The key for each item in the existing table will be rehashed and the item will be inserted into the new table

• If the new table is larger the hashing algorithm will need to be modified as it will need to generate a larger range of hash values

• Rehashing is also an opportunity to review the overall effectiveness of the hash function and to review how the collisions are handled

Hash Tables: Adding, Removing & Traversing Data

How do you add data to a hash table?

• To insert data into a hash table you use the hash function to generate the index of the position in the array that will be used to store the data

• The key must be stored as part of or alongside the data

• C6IA will be stored at position 65 

• To be sure this is possible, position 65 will be checked to see if it is empty. If it is, the new data item is inserted into this position

• If position 65 already contains data the overflow table will be used

  • This would take place by checking the first position in the overflow table to see if it is empty. 

  • If it is not empty, it will iterate through the table until an empty position is found. 

Algorithm for adding to a hash table

• Below is the pseudocode for the algorithm

FUNCTION hash_function(key, table_size): // Compute the hash value for the given key hash_value = key MOD table_size RETURN hash_value FUNCTION add_to_hash_table(hash_table, key, value, table_size): // Compute the hash value for the key using the hash function hash_value = hash_function(key, table_size) // Create a new entry with the key and value entry = (key, value) // Check if the hash value already exists in the hash table if hash_table[hash_value] is empty: // If the slot is empty, add the entry directly hash_table[hash_value] = [entry] else: // If the slot is not empty, handle collisions using a separate chaining approach // Append the entry to the existing list in the slot hash_table[hash_value].append(entry) ENDFUNCTION

How do you remove data from a hash table?

• To retrieve data from a hash table, the hash function is applied to the key to generate the index for the position within the array

• The key to B4YJ gives the hash value of 87

• The data can be retrieved in a single operation. You don’t need to use a binary or linear search, you can go to the correct position because an array allows direct access by index

• If the data item is found it is removed (the memory address is marked as available)

• If the data item is not found, then the overflow table is to be searched using the same linear approach mentioned above