graphs-traversing-adding-and-removing-data-

Graphs: Traversing, Adding & Removing Data

How do you traverse a graph?

• There are two approaches to traversing a graph:

  • A breadth-first search 

  • A depth-first search

Breadth-first search

• A breadth-first search is a graph traversal algorithm which systematically visits all neighbours of a given vertex before moving on to their neighbours. It then repeats this layer by layer.

• This method makes use of a queue data structure to enqueue each node as long as it is not already in a list of visited nodes. 

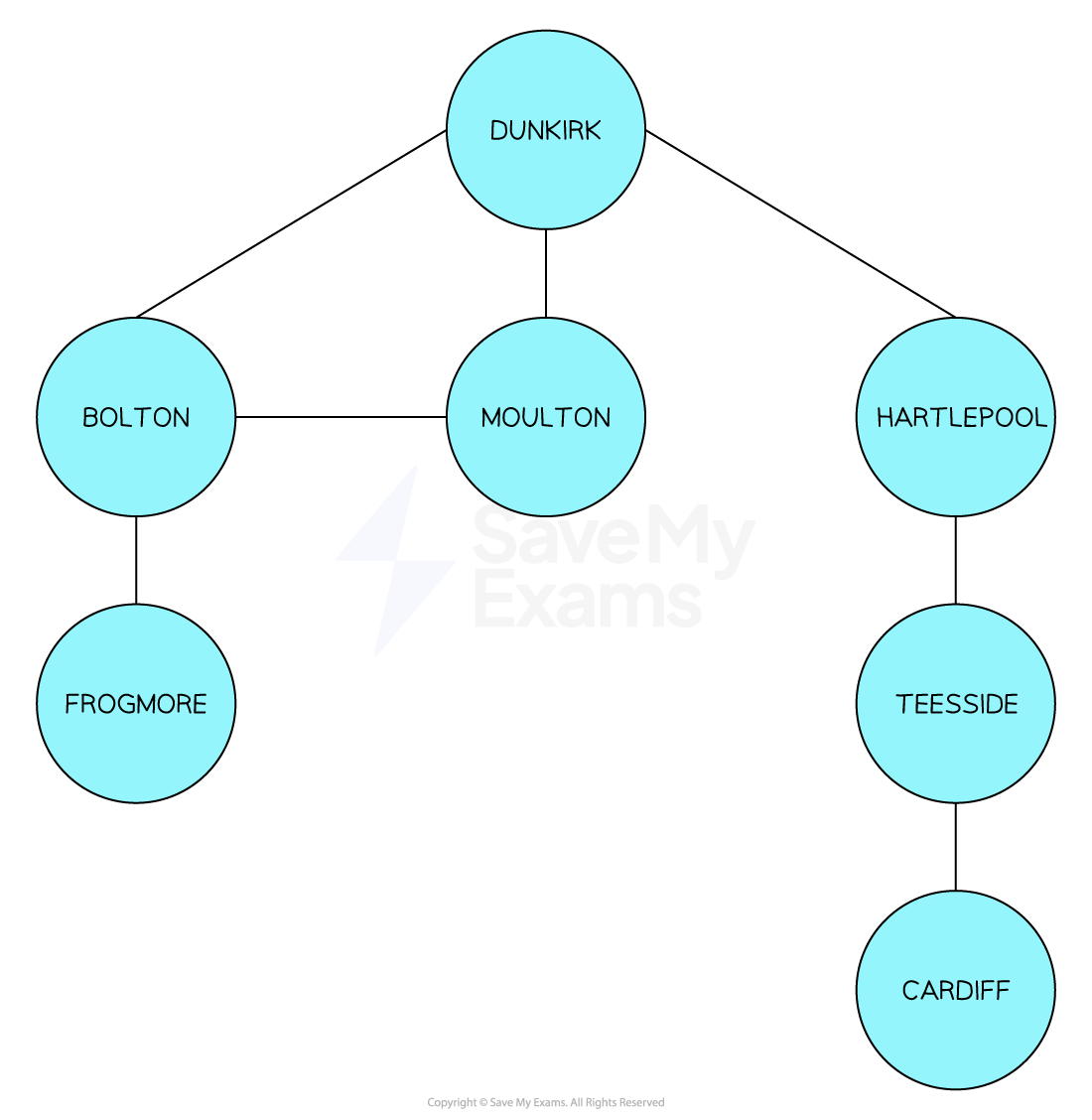
1. Take the example above, the root node, Dunkirk, would be set as the current node and then added to the visited list

1. Moving from left to right, we must check if the connected node isn’t already in the visited list, if it is not, it is enqueued to the queue. 

The first version of the queue would have appeared as

1. That linked vertex is then added to the visited list. Finally, it is removed from the queue as this process repeats. This means that all nodes, from left to right are enqueued to the queue in turn, before being added to the visited list, and then dequeued from the queue

2. Output all of the visited vertices

Our final visited list would appear as

The final version of the queue would have appeared as

Depth-first search

• In A Level Computer Science, a depth-first search is a graph traversal algorithm which uses an edge-based system

• This method makes use of a stack data structure to push each visited node onto the stack and then pop them from the stack when there are no nodes left to visit

Using the example from above, Dunkirk, would be set as the current node and then added to the visited list

1. Then check if the connected node isn’t already in the visited list, if it is not, it pushed to the stack. 

The first version of the stack would appear as

1. Next, any connected node that is not on the visited list is then pushed to the stack.

2. Then pop the stack to remove the item and set it as the current node.

3. Output all of the visited nodes

Our final visited list would appear as

You could visualise how the graph has been traversed below, with the left-most column first, then the middle, then the right-most column.

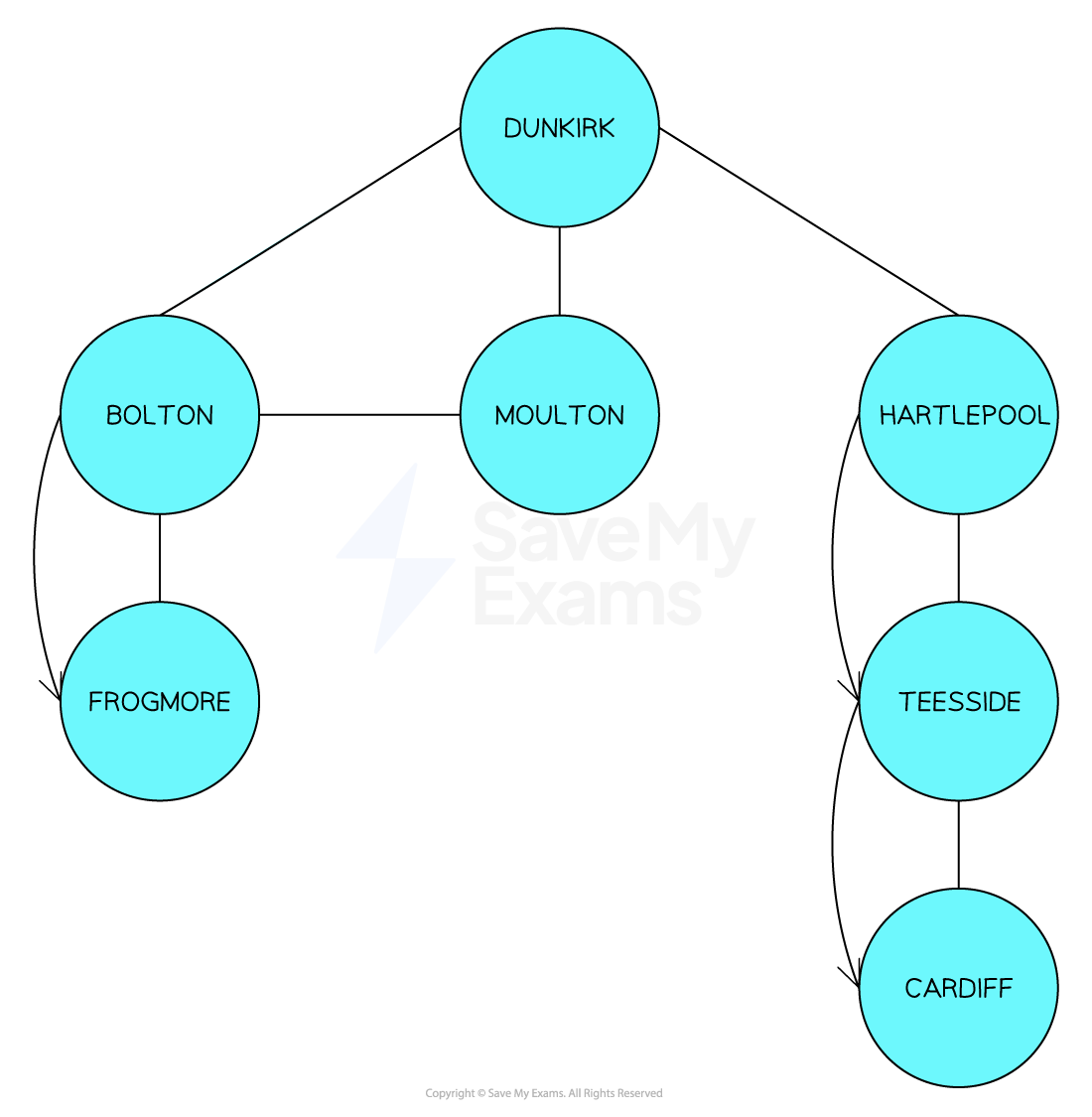
Adding & removing data in graphs

• There is no single algorithm for adding or deleting a node in a graph. This is because a graph can have a number of nodes connected to any number of other nodes.

• As a result, it is more important that there are a clear set of instructions to easily traverse the graph to find the specific node.

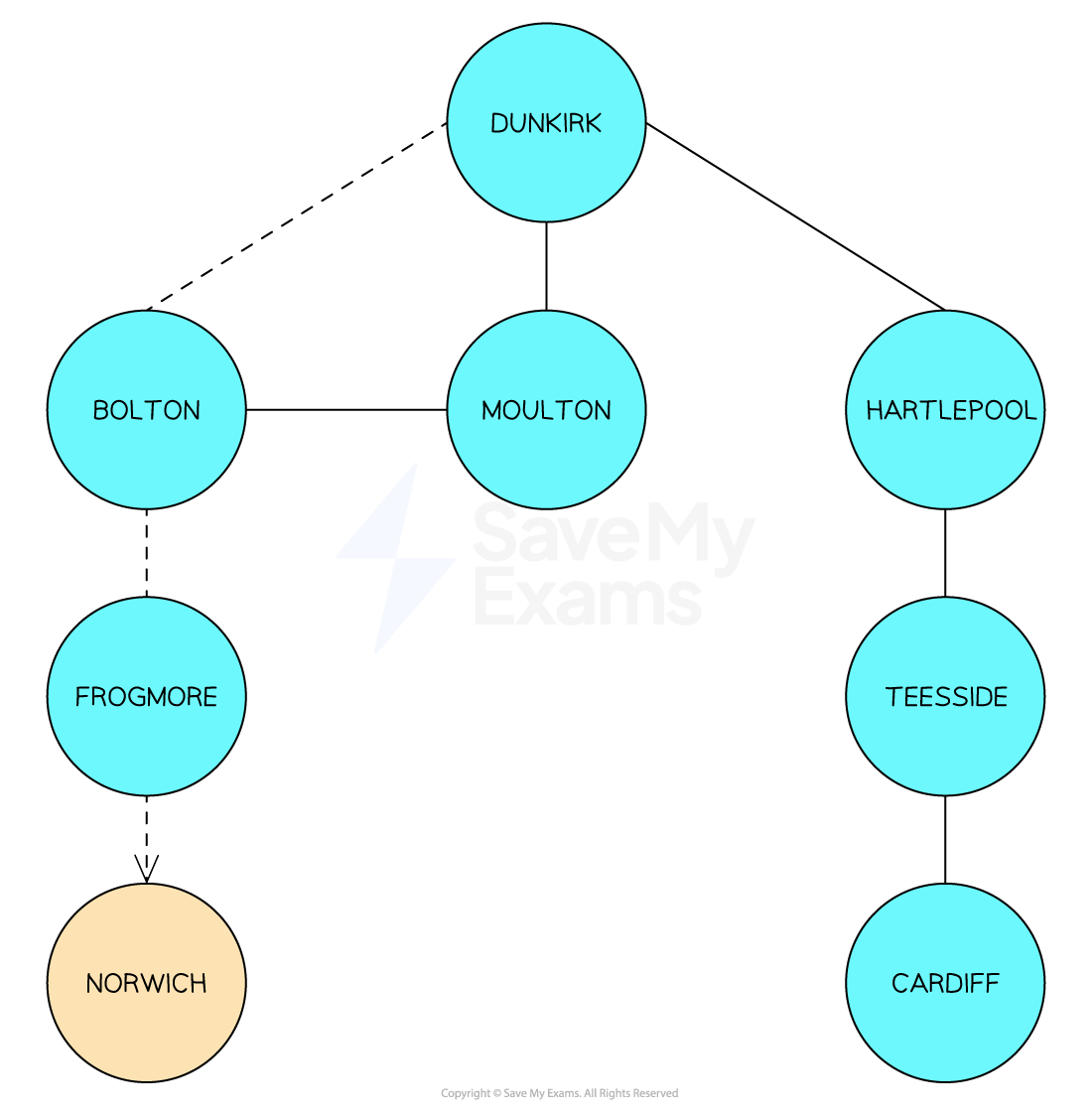
•  A Binary Tree is a special type of graph and it does have an algorithm for adding and deleting items. This is covered in the content titles’ Binary Search Trees’.