simplifying-boolean-algebra

What is Boolean algebra?

• In A Level Computer Science, Boolean algebra is a mathematical system used to manipulate Boolean values

• Complex expressions can be made simpler using the rules of Boolean algebra

• This is a more powerful simplification method than Karnaugh maps and can simplify expressions that Karnaugh maps cannot

• There are various different rules that you need to learn and that can then be applied to certain expressions to simplify them

• Combining these rules can mean that complex expressions can be reduced to much simpler ones

General rules

• General AND rules

  • X AND 0 = 0

  • X AND 1 = X

  • X AND A = X

  • NOT X AND X = 0

• Note, the value ox X is unknown and it is used as a placeholder. Therefore X AND 1 = X means that the output will be whatever the value of X is

• General OR rules

  • X OR 0 = X
    X OR 1 = 1
    X OR A = X
    NOT X OR X = 1

De Morgan’s Law

What is De Morgan’s Law?

• In A Level Computer Science, De Morgan’s Law is a strategy for simplifying expressions that include a negation of a conjunction or disjunction (simplifying by inverting all variable)

• NOT(A AND B) is the same as (NOT A) OR (NOT B)

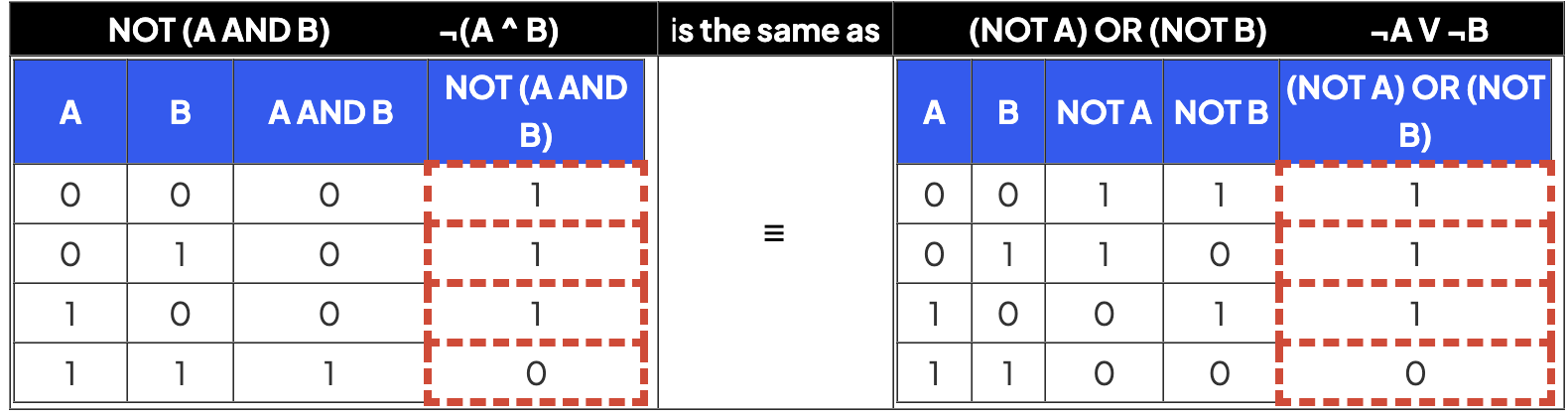
• Step 1

  • Change AND to OR (or vice versa) – ¬(A V B)

• Step 2

  • NOT the terms either side of the operator – ¬(¬A V ¬B)

• Step 3

  • NOT everything that has changed – ¬¬(¬A V ¬B)

• Step 4

  • Get rid of any double negation – (¬A V ¬B)

• Step 5

  • Remove any unnecessary brackets – ¬A V ¬B

• NOT(A OR B) is the same as (NOT A) AND (NOT B)

• Step 1

  • Change AND to OR (or vice versa) – ¬(A ^ B)

• Step 2

  • NOT the terms either side of the operator – ¬(¬A ^ ¬B)

• Step 3

  • NOT everything that has changed – ¬¬(¬A ^ ¬B)

• Step 4

  • Get rid of any double negation – (¬A ^ ¬B)

• Step 5

  • Remove any unnecessary brackets – ¬A ^ ¬B

• Simplifying using this law allows the use of only NAND or NOR gates which makes building microprocessors much easier (i.e. Flash drives)

Distribution

What is distributive law?

• This explains how AND and OR interact with each other

• This is a bit like factorising in normal maths

• A AND (B OR C) is the same as (A AND B) OR (A AND C)

• A OR (B AND C) is the same as (A OR B) AND (A OR C

Real-life example

• “You can pick one subject from group A and either one from group B or group C“

• is the same as

• “You can pick one subject from group A and one from group B or one subject from group A and one from group C“

Association

What is associative law?

• This explains how variables associate in expressions of more than two variables

• Allows us to remove brackets and regroup variables

• (A AND B) AND C is the same as A AND (B AND C) is the same as A AND B AND C

• (A OR B) OR C is the same as A OR (B OR C) is the same as A OR B OR C

Real-life example

• “Zarmeen and her friends, Zahra and Ella have been chosen to represent the school”

• is the same as

• “Zarmeen and Zahra, and their friend Ella have been chosen to represent the school”

• is the same as

• “Zarmeen, Zahra and Ella have been chosen to the represent the school”

Commutation

What is commutative law?

• States that the order of the variables does not change the truth value of the expression

• A AND B is the same as B AND A

• A OR B is the same as B OR A

Real-life example

• “Fynn and George won gold medals”

• is the same as

• George and Fynn won gold medals”

Double Negation

What is double negation law?

• States that the double negation of a variable results in the original variable

• NOT(NOT(A)) = A

Real-life example

• “I don’t not want to visit the castle”

• is the same as 

• “I do want to visit the castle”