3-3-4-critical-path-analysis

The nature and purpose of critical path analysis

• Critical path analysis is a project management tool that uses network analysis to plan complex and time-sensitive projects 

• Critical path analysis involves the construction of a visual model of the project that includes key elements:

  • A list of all activities required to complete the project

  • The time (duration) that each activity will take to complete

  • How each project activity depends on others

• Critical path analysis shows:

  • The order in which activities must be completed

  • The longest path of project activities to the completion of the project

  • The earliest and latest that each project activity can start and finish without delaying completion of the project as a whole

  • Activities within a project that can be carried out simultaneously

  • The critical project activities that, if delayed, will cause the project as a whole to overrun

  • Those project activities where some delay is acceptable without delaying the project as a whole

  • The shortest time possible to complete the project

• It allows managers to identify the relationships between the activities involved and to work out the most efficient way of completing the project

  • Resources such as raw materials and components can be ordered or hired at precisely the right time they are needed

  • Working capital may be managed efficiently

  • Where delays occur, managers can identify the implications for the project’s completion and redirect resources if required 

Drawing critical path analysis diagrams

Components of network analysis diagrams

Example network diagram

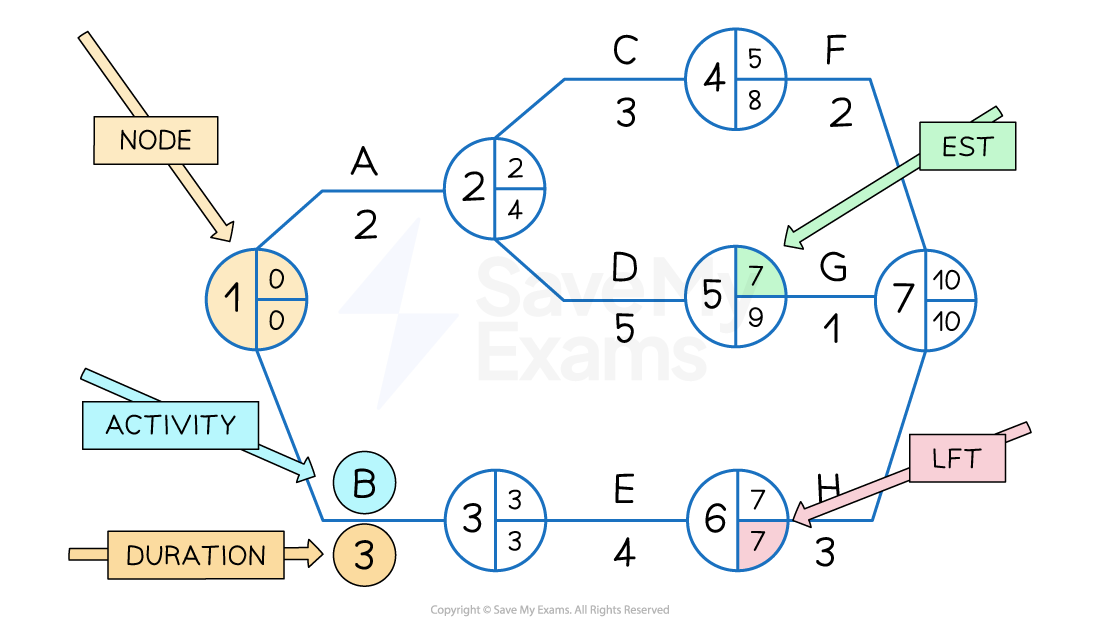
• A network diagram must always start and end at a single node

• Lines must not cross and must only be assigned to activities

Critical path calculations

Earliest start times

• Working forwards from Node 1, it is possible to calculate the earliest start time (EST) for each activity by adding the duration of each task

• The EST for each activity is placed in the top right of each node

  • Node 1 is the starting point of the project and where both Activity A and Activity B begin

  • Activity A and Activity B are independent processes

  • Activity A has a duration of two days, and its EST is zero days

  • Activity B has a duration of three days, and its EST is also zero days

  • Activity C and Activity D both begin at Node 2 and are dependent upon the completion of Activity A but are independent from each other

    • Activity C has a duration of three days, and its EST is two days 

    • Activity D has a duration of five days, and its EST is also two days

  • Activity E begins at Node 3

    • Activity E has a duration of four days, and its EST is three days

  • Activity F begins at Node 4

    • Activity F has a duration of two days, and its EST is five days

  • Activity G begins at Node 5

    • Activity G has a duration of one day, and its EST is seven days

  • Activity H begins at Node 6

    • Activity H has a duration of three days, and its EST is seven days

  • Node 7 is the endpoint of the project

Latest finish times

• Working backwards from Node 7, it is now possible to calculate the latest finish time (LFT) for each activity by subtracting the duration of each task

• The LFT for each activity is placed in the bottom right of each node

  • Node 7 is the endpoint of the project, which has an LFT of ten days

  • Activity H has a duration of three days

    • The LFT in Node 6 is seven days (10 days − 3 days)

  • Activity G has a duration of one day

    • The LFT in Node 5 is nine days (10 days − 1 day)

  • Activity F has a duration of two days

    • The LFT in Node 4 is eight days (10 days − 2 days)

  • Activity E has a duration of four days

    • The LFT in Node 3 is three days (7 days − 4 days)

  • Activity D has a duration of five days

    • The LFT in Node 2 is four days (9 days − 5 days)

  • Activity C has a duration of three days

    • The LFT in Node 3 is four days because Activity D is the more time-critical of the two activities that are dependent upon the completion of Activity A, so its LFT is recorded

  • Activity B has a duration of three days

    • The LFT in Node 1 is zero days (3 days − 3 days)

  • Activity A has a duration of two days

    • The LFT in Node 1 is zero days because Activity B is the more time-critical of the two starting activities, so its LFT is recorded

• The LFT in Node 1 is always zero

Identifying the critical path

• The critical path highlights those activities that determine the length of the whole project

  • If any of these critical activities are delayed, the project as a whole will be delayed

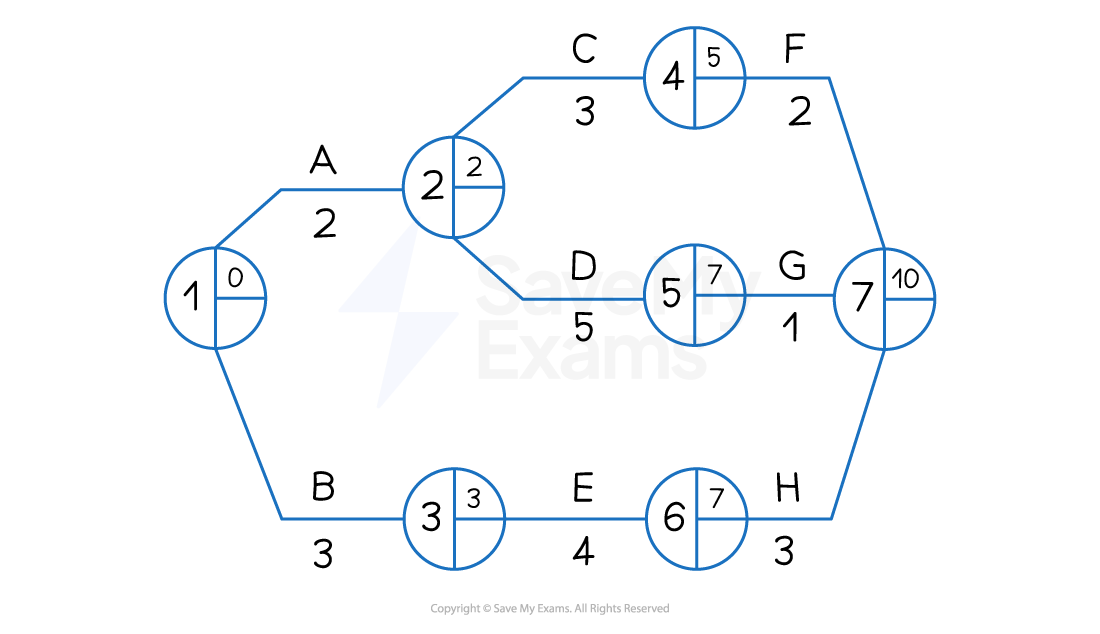
  • The critical path follows the nodes where the EST and LFT are equal

    • In the diagram below, Nodes 1, 3, 6 and 7 have equal ESTs and LFTs

    • Activities that determine these nodes are B, E and H

    • These activities are marked with two short lines

    • The critical path is therefore BEH

Identifying and calculating float time

• Float time exists where there is a difference between the EST and the LFT

• Where float time is identified, managers may:

  • Transfer resources, such as staff or machinery, to more critical activities

  • Allow extra time to complete tasks to improve quality or allow for creativity