operations-planning

The need for operations planning

• Operations planning is the process of organising all the resources and activities needed to produce goods or services efficiently

  • It ensures that the right products are made, at the right time, in the right quantity and using the right resources

Benefits of operations planning

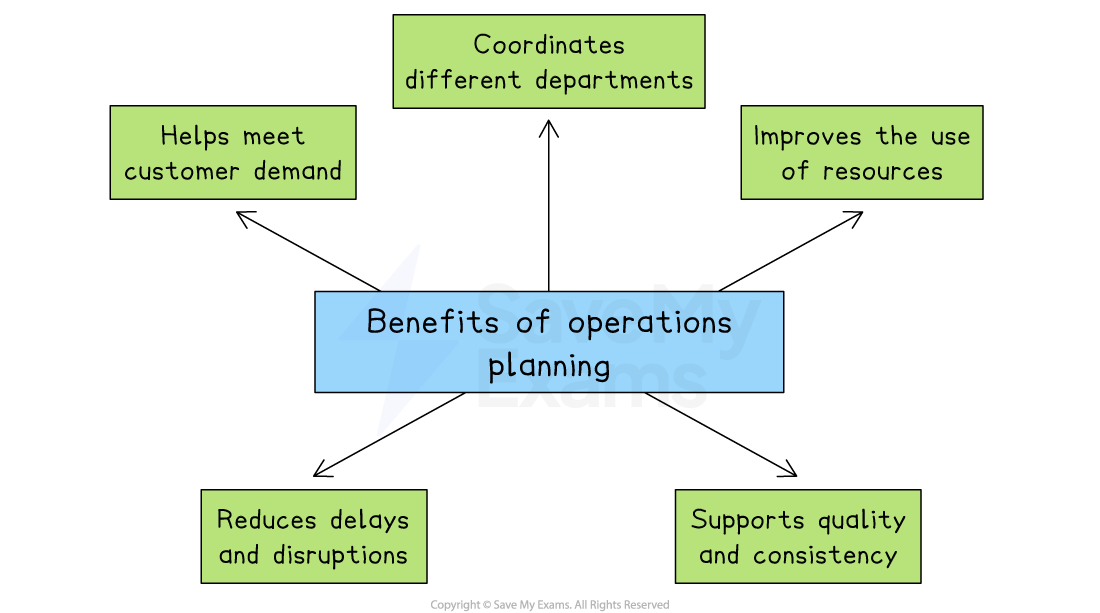
• Meet customer demand

  • Planning helps businesses produce the correct quantity of goods to match expected demand

    • Without it, a business might make too little, causing stock shortages and lost sales,or too much, leading to waste and higher costs

• Improve the use of resources

  • Operations planning ensures that staff, machinery and materials are used efficiently

    • It helps avoid wasted time, overuse of equipment, or running out of stock during production

• Coordination of departments

  • Good planning allows production, purchasing, finance, and marketing to work together

    • E.g. Marketing can give sales forecasts, finance can set budgets and production can schedule output to meet targets

• Reduces delays and disruptions

  • Planning helps identify potential problems early, such as a shortage of raw materials or a machine breakdown

    • Solutions can be prepared in advance, reducing the risk of disruption

• Supports quality and consistency

  • Operations planning includes setting clear standards for quality, timing and workflows

    • This ensures that products or services are delivered consistently to meet customer expectations

An introduction to network diagrams

• A network diagram is a visual planning tool used in operations management to help organise and schedule tasks in a project

• It shows the order in which activities must be completed and how long each one is expected to take

Example network analysis

• A network diagram must always start and end on a single node

• Lines must not cross and must only be assigned to activities

How network diagrams help operations planning

• Network diagrams improve time management by helping managers identify the critical path, the shortest time needed to complete a project

  • They highlight task dependencies by showing which activities must be completed before others can begin, helping to avoid mistakes and delays

• Network diagrams support efficient resource allocation by showing when people, machines, or materials will be needed, reducing idle time and bottlenecks

  • They improve decision-making by making it easier to adjust plans if there are unexpected delays or changes to deadlines

Elements of network diagrams

Node

• A node is a circle that represents a point in time where an activity either starts or finishes

• Each node is split into three sections

  • The left half of the circle shows the activity number

  • The top right section shows the earliest start time (EST)—the earliest point an activity can begin, based on the completion of the previous activity

  • The bottom right section shows the latest finish time (LFT)—the latest time by which the previous activity must be completed without delaying the project

Activities

• An activity is a task or process within a project that takes time to complete

  • Activities are shown on a network diagram as a line linking two nodes

  • Above the line, you will usually find either a letter or a short description of the activity

Duration

• The duration is the length of time required to complete an activity

• This is shown below the activity line and is usually measured in time units such as hours or days

Dummy activities

• A dummy activity is an activity that has a weight of zero

  • Dummies are not assigned names (letters)

  • Dummies are represented by dotted lines

Where a dummy activity is used

• To ensure each activity has a unique pair of start and end nodes

  • E.g. In the activity network below, activity D has immediate predecessors B and C

    • B and C cannot both start at event (node) 1 and end at event (node) 2 (this would not be a unique pair)

    • a dummy activity is used so that B has start and end pair (1, 3) and C has a start and end pair (1, 2)

• When there is a split of immediate predecessors

  • E.g. In the activity network below, activity D has immediate predecessors B and C

    • Activity E only has B as an immediate predecessor

    • A dummy activity is used to show that D depends on both B and C

Using network diagrams for critical path analysis

1. Calculating earliest start times (EST)

• Working forward from Node 1, it is possible to calculate the Earliest Start Time for each activity by adding the duration of each task

• The EST for each activity is placed in the top right of each node

  • Node 1 is the starting point of the project and where both Activity A and Activity B begin

  • Activity A and Activity B are independent processes

  • Activity A has a duration of 2 days and its earliest start time (EST) is 0 days

  • Activity B has a duration of 3 days and its EST is also 0 days

  • Activity C and Activity D both begin at Node 2 and are dependent upon the completion of Activity A but are independent from each other

    • Activity C has a duration of 3 days and its EST is 2 days 

    • Activity D has a duration of 5 days and its EST is also 2 days

• Activity E begins at Node 3

  • Activity E has a duration of 4 days and its EST is 3 days

• Activity F begins at Node 4

  • Activity F has a duration of 2 days and its EST is 5 days

• Activity G begins at Node 5

  • Activity G has a duration of 1 day and its EST is 7 days

• Activity H begins at Node 6

  • Activity H has a duration of 3 days and its EST is 7 days

• Node 7 is the end point of the project

2. Calculating latest finish times (LFT)

• Working backwards from Node 7, it is now possible to calculate the Latest Finish Time (LFT) for each activity by subtracting the duration of each task