WEILAI Online Academic assistant
WEILAI Online Academic assistant
Back to 课程

Biology_A-level_Cie

0% Complete
0/0 Steps
  1. 1-1-the-microscope-in-cell-studies
    5 主题
  2. 1-2-cells-as-the-basic-units-of-living-organisms
    5 主题
  3. 2-1-testing-for-biological-molecules
    3 主题
  4. 2-2-carbohydrates-and-lipids
    8 主题
  5. 2-3-proteins
    6 主题
  6. 2-4-water
    2 主题
  7. 3-1-mode-of-action-of-enzymes
    5 主题
  8. 3-2-factors-that-affect-enzyme-action
    8 主题
  9. 4-1-fluid-mosaic-membranes
    4 主题
  10. 4-2-movement-into-and-out-of-cells
    12 主题
  11. 5-1-replication-and-division-of-nuclei-and-cells
    6 主题
  12. 5-2-chromosome-behaviour-in-mitosis
    2 主题
  13. 6-1-structure-of-nucleic-acids-and-replication-of-dna
    4 主题
  14. 6-2-protein-synthesis
    5 主题
  15. 7-1-structure-of-transport-tissues
    4 主题
  16. 7-2-transport-mechanisms
    7 主题
  17. 8-1-the-circulatory-system
    7 主题
  18. 8-2-transport-of-oxygen-and-carbon-dioxide
    5 主题
  19. 8-3-the-heart
    4 主题
  20. 9-1-the-gas-exchange-system
    6 主题
  21. 10-1-infectious-diseases
    3 主题
  22. 10-2-antibiotics
    3 主题
  23. 11-1-the-immune-system
    4 主题
  24. 11-2-antibodies-and-vaccination
    6 主题
  25. 12-1-energy
    5 主题
  26. 12-2-respiration
    11 主题
  27. 13-1-photosynthesis-as-an-energy-transfer-process
    8 主题
  28. 13-2-investigation-of-limiting-factors
    2 主题
  29. 14-1-homeostasis-in-mammals
    8 主题
  30. 14-2-homeostasis-in-plants
    3 主题
  31. 15-1-control-and-coordination-in-mammals
    12 主题
  32. 15-2-control-and-coordination-in-plants
    3 主题
  33. 16-1-passage-of-information-from-parents-to-offspring
    5 主题
  34. 16-2-the-roles-of-genes-in-determining-the-phenotype
    7 主题
  35. 16-3-gene-control
    3 主题
  36. 17-1-variation
    4 主题
  37. 17-2-natural-and-artificial-selection
    7 主题
  38. 17-3-evolution
    2 主题
  39. 18-1-classification
    5 主题
  40. 18-2-biodiversity
    7 主题
  41. 18-3-conservation
    6 主题
  42. 19-1-principles-of-genetic-technology
    11 主题
  43. 19-2-genetic-technology-applied-to-medicine
    4 主题
  44. 19-3-genetically-modified-organisms-in-agriculture
    2 主题
  45. 1-1-the-microscope-in-cell-studies
  46. 1-2-cells-as-the-basic-units-of-living-organisms
  47. 2-1-testing-for-biological-molecules
  48. 2-2-carbohydrates-and-lipids
  49. 2-3-proteins
  50. 2-4-water
  51. 3-1-mode-of-action-of-enzymes
  52. 3-2-factors-that-affect-enzyme-action
  53. 4-1-fluid-mosaic-membranes
  54. 4-2-movement-into-and-out-of-cells
  55. 5-1-replication-and-division-of-nuclei-and-cells
  56. 5-2-chromosome-behaviour-in-mitosis
  57. 6-1-structure-of-nucleic-acids-and-replication-of-dna
  58. 6-2-protein-synthesis
  59. 7-1-structure-of-transport-tissues
  60. 7-2-transport-mechanisms
  61. 8-1-the-circulatory-system
  62. 8-2-transport-of-oxygen-and-carbon-dioxide
  63. 8-3-the-heart
  64. 9-1-the-gas-exchange-system
  65. 10-1-infectious-diseases
  66. 10-2-antibiotics
  67. 11-1-the-immune-system
  68. 11-2-antibodies-and-vaccination
课 Progress
0% Complete

Pearson’s linear correlation

  • When recording the abundance and distribution of species in an area different trends may be observed

  • Sometimes correlation between two variables can appear in the data

    • Correlation is an association or relationship between variables

    • There is a clear distinction between correlation and causation: a correlation does not necessarily imply a causative relationship

    • Causation occurs when one variable has an influence on, or is influenced by, another

  • There may be a correlation between species; for example, two species always occurring together

  • There may be a correlation between a species and an abiotic factor, for example, a particular plant species and the soil pH

  • The apparent correlation between variables can be analysed using scatter graphs and different statistical tests

Correlation between variables

  • In order to get a broad overview of the correlation between two variables the data points for both variables can be plotted on a scatter graph

  • The correlation coefficient (r) indicates the strength of the relationship between variables

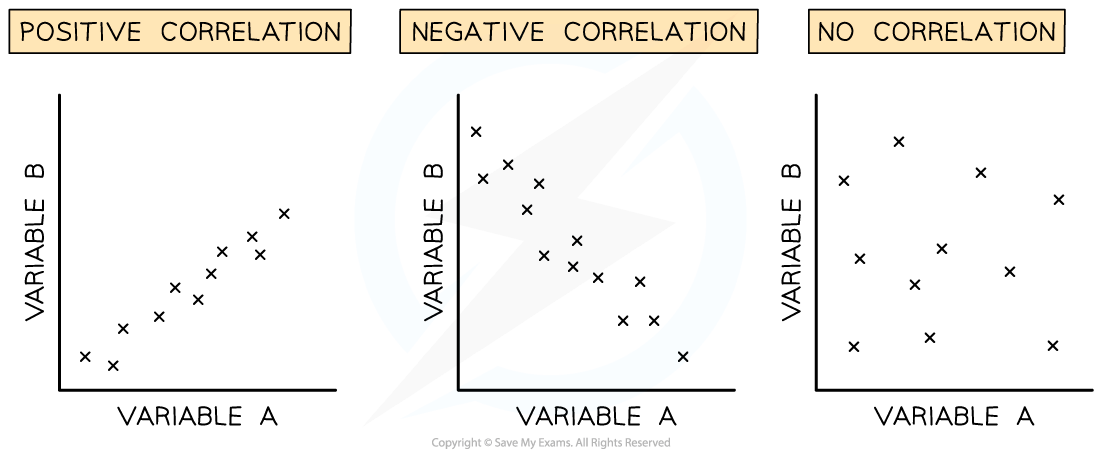
  • Perfect correlation occurs when all of the data points lie on a straight line with a correlation coefficient of 1.0 or -1.0

  • Correlation can be positive or negative

    • Positive correlation: as variable A increases, variable B increases

    • Negative correlation: as variable A increases, variable B decreases

  • If there is no correlation between variables the correlation coefficient will be 0

Three scatter plots show positive, negative, and no correlation between variables A and B, with points distributed accordingly in each plot.
Different types of correlation in scatter graphs

  • The correlation coefficient (r) can be calculated to determine whether a linear relationship exists between variables and how strong that relationship is

Pearson’s linear correlation

  • Pearson’s linear correlation is a statistical test that determines whether there is linear correlation between two variables

  • The data must:

    • Be quantitative, e.g. the number of individuals has been counted and a numerical value recorded

    • Show a linear relationship upon visual inspection

    • Show a normal distribution

  • Method:

    • Step 1: Create a scatter graph of data gathered and identify if a linear correlation exists

    • Step 2: State a null hypothesis

    • Step 3:  Use the following equation to work out Pearson’s correlation coefficient r

Pearsons Equation, downloadable AS & A Level Biology revision notes

Where:

  • r = correlation coefficient

  • x = number of species A

  • y = number of species B

  • n = number of readings

  • Sx = standard deviation of species A

  • Sy = standard deviation of species B

  • x̄= mean number of species A

  • ȳ= mean number of species B

  • If the correlation coefficient r is close to 1.0 or -1.0 then it can be stated that there is a strong linear correlation between the two variables and the null hypothesis can be rejected

Worked Example

Some students used quadrats to measure the abundance of different plant species in a garden. They noticed that two particular species seemed to occur alongside each other. They plotted a scatter graph and the data they collected had no major outliers and showed roughly normal distribution.

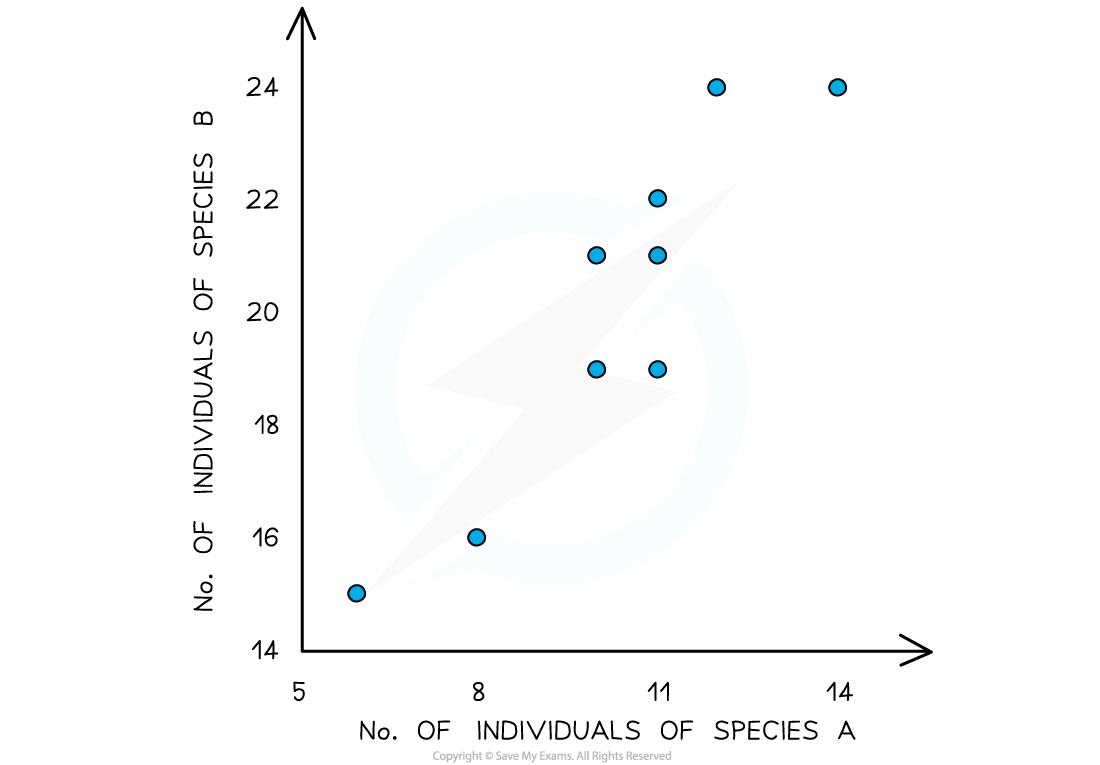
Scatter plot showing number of individuals of species A on X-axis and species B on Y-axis, with data points indicating various combinations.
Scatter graph showing the linear correlation between the abundance of species A and B. It shows linear correlation and so is suitable for analysis by Pearson’s correlation coefficient.

Investigate the possible correlation using Pearson’s linear correlation coefficient.

Null hypothesis: There is no correlation between the abundance of species A and species B.

Steps to calculate the correlation coefficient:

Step 1: Calculate xy

Step 2: Calculate x̅ and y̅ (these are the means of x and y)

Step 3: Calculate nx̅y̅

Step 4: Find ∑xy

Step 5: Calculate standard deviation for each set of data Sx  and Sy

Step 6: Substitute the appropriate numbers into the equation

Pearsons Equation, downloadable AS & A Level Biology revision notes
<td class=”border border-dark ContentBlock_tableCell__N2pb_” col

Quadrat

No. of individuals of species A (x)

No. of individuals of species B (x)

xy

1

10

21

210

2

11

19

209

3

11

22

242

4

6

15

90

5

8

16

128

6

14

24

336

7

10

19

190

8

12

24

288

9

11

21

231

10

10

19

190

Mean

x̄ = 10.3

ȳ = 20

∑xy = 2114

nx̄ȳ

10 × 10.3 × 20 = 2060