课 24, 主题 8

In Progress

← Previous Next→

4-6-8-mean-and-standard-deviation

课 Progress

0% Complete

Exam code:7401

Calculating mean values & standard deviation

Descriptive statistics are invaluable when interpreting data from experiments
Some experiments have thousands or millions of data values/observations, and descriptive statistics allow for sample data to be summarised in a concise manner

Mean

A mean value is what is usually meant by “an average” in biology

mean = sum of all measurements ÷ number of measurements

Problems with the mean occur when a dataset contains extreme, or outlying values, which can make the mean too high or too low to represent the data
The mean is sometimes referred to as X̄ in calculations

Worked Example

Fifteen rats were timed to see how long it took them to reach the end of a maze puzzle. Their times, in seconds, are given below.

Calculate the mean time.

12, 10, 15, 14, 17,

11, 12, 13, 9, 21,

14, 20, 19, 16, 23

Answer:

Step 1: calculate the mean

12 + 10 + 15 + 14 + 17 + 11 + 12 + 13 + 9 + 21 + 14 + 20 + 19 + 16 + 23 = 226

226 ÷ 15 = 15.067

Step 2: round to 3 significant figures

Mean (X̄) = 15.1 seconds

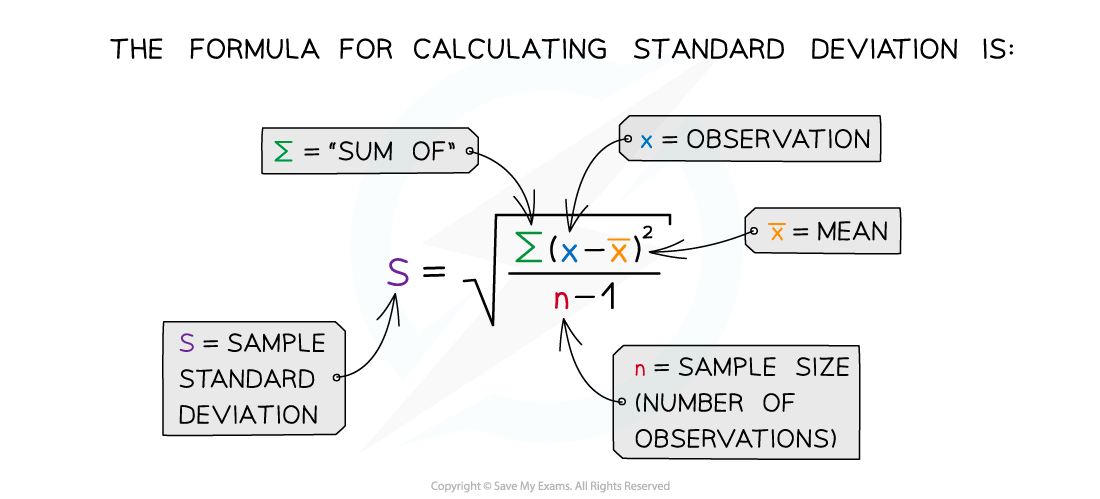
Standard deviation

The mean is a more informative statistic when it is provided alongside standard deviation
Standard deviation measures the spread of data around the mean value
- It is useful when comparing consistency between different data sets
The mean must be calculated before working out the standard deviation

Examiner Tips and Tricks

You will not be required to calculate standard deviations in written papers, but you may need to calculate the standard deviation as part of practical work and investigations. You must understand what the standard deviation tells you about a data set as you may be asked to interpret mean values and their standard deviations.

Worked Example

The ear lengths of a population of rabbits were measured:

Ear length (mm)

62, 60, 59, 61, 60, 58, 59, 60, 57, 56, 59, 58, 60, 59, 57

Calculate the mean and standard deviation.

Step 1: calculate the mean

mean = 885 ÷ 15 = 59 mm

Step 2: find the difference between each value and the mean

Subtract the mean from each value to find the difference
Example:

62 – 59 = 3

Step 3: square each difference (to remove any negative values)

Example:

3² = 9

Step 4: total the differences

Difference between value and mean (x – x̄)	Difference between value and mean squared (x – x̄)²
62 – 59 = 3	9
60 – 59 = 1	1
59 – 59 = 0	0
61 – 59 = 2	4
60 – 59 = 1	1
58 – 59 = -1	1
59 – 59 = 0	0
60 – 59 = 1	1
57 – 59 = -2	4
56 – 59 = -3	9
59 – 59 = 0	0
58 – 59 = -1	1
60 – 59 = 1	1
59 – 59 = 0	0
57 – 59 = -2	4
Sum of (x – x̄)²	36

Step 5: divide the total by (n-1) to get value A

36 ÷ (15 – 1)

= 36 ÷ 14

= 2.571

Step 6: determine the square root of value A

$square root of 2.571 end root$ = 1.604

Standard deviation = 1.60

This value is small compared to the mean value (59 mm), indicating that there is little spread around the mean.

Biology AS AQA

4-6-8-mean-and-standard-deviation

Calculating mean values & standard deviation

Mean

Worked Example

Standard deviation

Examiner Tips and Tricks

Worked Example

Responses