Biology AS AQA
-
1-1-biological-molecules-carbohydrates11 主题
-
1-1-1-biological-molecules-key-terms
-
1-1-2-biological-molecules-reactions
-
1-1-3-monosaccharides
-
1-1-4-glucose
-
1-1-5-the-glycosidic-bond
-
1-1-6-chromatography-monosaccharides
-
1-1-7-disaccharides
-
1-1-8-starch-and-glycogen
-
1-1-9-cellulose
-
1-1-10-biochemical-tests-sugars-and-starch
-
1-1-11-finding-the-concentration-of-glucose
-
1-1-1-biological-molecules-key-terms
-
1-2-biological-molecules-lipids3 主题
-
1-3-biological-molecules-proteins5 主题
-
1-4-proteins-enzymes12 主题
-
1-4-1-many-proteins-are-enzymes
-
1-4-2-enzyme-specificity
-
1-4-3-how-enzymes-work
-
1-4-4-required-practical-measuring-enzyme-activity
-
1-4-5-drawing-a-graph-for-enzyme-rate-experiments
-
1-4-6-using-a-tangent-to-find-initial-rate-of-reaction
-
1-4-7-limiting-factors-affecting-enzymes-temperature
-
1-4-8-limiting-factors-affecting-enzymes-ph
-
1-4-10-limiting-factors-affecting-enzymes-enzyme-concentration
-
1-4-11-limiting-factors-affecting-enzymes-substrate-concentration
-
1-4-12-limiting-factors-affecting-enzymes-inhibitors
-
1-4-14-control-of-variables-and-uncertainty
-
1-4-1-many-proteins-are-enzymes
-
1-5-nucleic-acids-structure-and-dna-replication8 主题
-
1-5-2-nucleotide-structure-and-the-phosphodiester-bond
-
1-5-3-dna-structure-and-function
-
1-5-4-rna-structure-and-function
-
1-5-5-ribosomes
-
1-5-6-the-origins-of-research-on-the-genetic-code
-
1-5-8-the-process-of-semi-conservative-replication
-
1-5-9-calculating-the-frequency-of-nucleotide-bases
-
1-5-10-the-watson-crick-model
-
1-5-2-nucleotide-structure-and-the-phosphodiester-bond
-
1-6-atp-water-and-inorganic-ions4 主题
-
2-1-cell-structure7 主题
-
2-2-the-microscope-in-cell-studies4 主题
-
2-3-cell-division-in-eukaryotic-and-prokaryotic-cells8 主题
-
2-4-cell-membranes-and-transport9 主题
-
2-4-1-the-structure-of-cell-membranes
-
2-4-3-the-cell-surface-membrane
-
2-4-4-diffusion
-
2-4-5-osmosis
-
2-4-7-osmosis-in-animal-cells
-
2-4-9-required-practical-investigating-water-potential
-
2-4-10-active-transport-and-co-transport
-
2-4-11-adaptations-for-rapid-transport
-
2-4-13-required-practical-factors-affecting-membrane-permeability
-
2-4-1-the-structure-of-cell-membranes
-
2-5-cell-recognition-and-the-immune-system7 主题
-
2-6-vaccines-disease-and-monoclonal-antibodies6 主题
-
3-1-adaptations-for-gas-exchange6 主题
-
3-2-human-gas-exchange14 主题
-
3-2-5-the-alveolar-epithelium
-
3-2-1-the-human-gas-exchange-system
-
3-2-2-dissecting-the-gas-exchange-system
-
3-2-3-microscopy-and-gas-exchange-surfaces
-
3-2-4-investigating-gas-exchange
-
3-5-5-investigating-heart-rate
-
3-5-6-blood-vessels
-
3-5-7-capillaries-and-tissue-fluid
-
3-5-8-cardiovascular-disease-data
-
3-2-10-risk-factor-data
-
3-2-11-correlations-and-causal-relationships
-
3-2-6-ventilation-and-gas-exchange
-
3-2-8-the-effects-of-lung-disease
-
3-2-9-pollution-and-smoking-data
-
3-2-5-the-alveolar-epithelium
-
3-3-digestion-and-absorption5 主题
-
3-4-mass-transport-in-animals6 主题
-
3-5-the-circulatory-system-in-animals4 主题
-
3-6-mass-transport-in-plants6 主题
-
4-1-dna-genes-and-chromosomes10 主题
-
4-2-dna-and-protein-synthesis3 主题
-
4-3-genetic-diversity-mutations-and-meiosis7 主题
-
4-4-genetic-diversity-and-adaptation6 主题
-
4-5-species-and-taxonomy4 主题
-
4-6-biodiversity9 主题
4-6-7-quantitative-investigations-of-variation
Exam code:7401
Quantitative investigations of variation
-
Quantitative investigations of variation can involve using measures of central tendency such as the mean values and their standard deviations
-
A mean value describes the average value of a data set
-
Standard deviation is a measure of the spread or dispersion of data around the mean
-
A small standard deviation indicates that the results lie close to the mean (less variation)
-
A large standard deviation indicates that the results are more spread out
-
-
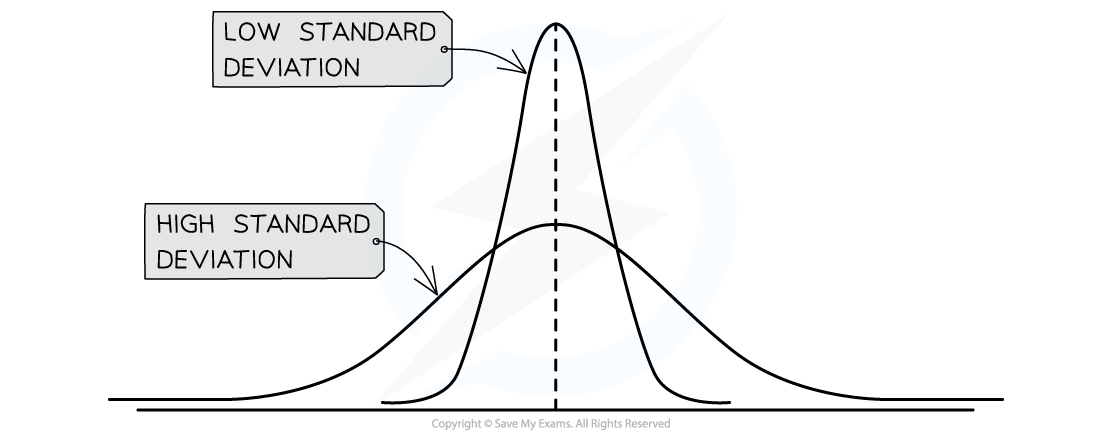
Comparison between groups
-
When comparing the results from different groups or samples, using a measure of central tendency, such as the mean, can be quite misleading
-
For example, looking at the two groups below:
-
Group A: 2, 15, 14, 15, 16, 15, 14; mean = 13
-
Group B: 1, 3, 10, 15, 20, 22, 20; mean = 13
-
-
Even though both groups have a mean of 13, most of the values in Group A lie close to the mean, whereas in Group B, most values lie quite far from the mean
-
For comparison between groups or samples, it is better practice to use the standard deviation in conjunction with the mean
-
The standard deviations of different data sets can determine whether observed differences are due to real effects or just natural variation
-
If standard deviations overlap, the difference between data sets is not statistically significant
-
If standard deviations do not overlap, the difference is likely statistically significant
-
Worked Example
A group of scientists wanted to investigate the effects of a specific diet on the risk of coronary heart disease. One group was given a specific diet for 8 weeks, while the other group acted as a control. After 8 weeks, scientists measured the diameter of the lumen of the main artery in the arm of the volunteers. The results of the experiment are shown in Table 1 below:
|
Mean maximum diameter of lumen of main aterty in the arm (mm) |
||
|---|---|---|
|
Experimental group (± standard deviation) |
Control group (± standard deviation) |
|
|
Before experiment |
0.69 (± 0.02) |
0.71 (± 0.02) |
|
After 8 weeks |
0.74 (± 0.03) |
0.72 (± 0.05) |
Use the standard deviations to evaluate whether the diet had a significant effect.
[2 marks]
Step one: Find the full range of values included within the standard deviations for each data set
Experimental group before: 0.67 to 0.71mm
Experimental group after: 0.71 to 0.77mm
Control group before: 0.69 to 0.73mm
Control group after: 0.67 to 0.77mm
Step two: Use this information to form your answer
0.67~0.71mm and 0.71~0.77mm overlap
There is an overlap of standard deviations in the experimental group before and after the experiment, so it can be said that the difference before and after the experiment is not significant; [1 mark]
0.71~0.77mm and 0.67~0.77mm
There is also an overlap of standard deviations between the experimental and control groups after the eight weeks, so it can be said that the difference between groups is not significant; [1 mark]
Examiner Tips and Tricks
The standard deviations of a data set are not always presented in a table, they can also be represented by standard deviation error bars on a graph. You will not be required to calculate standard deviations in written papers.

Responses