Maths Gcse Aqa Foundation
-
Scatter-Graphs-And-Correlation Aqa Foundation2 主题
-
Statistical-Diagrams Aqa Foundation6 主题
-
Averages-Ranges-And-Data Aqa Foundation7 主题
-
Tree-Diagrams-And-Combined-Probability Aqa Foundation2 主题
-
Simple-Probability-Diagrams Aqa Foundation4 主题
-
Transformations Aqa Foundation4 主题
-
Vectors Aqa Foundation3 主题
-
Pythagoras-And-Trigonometry Aqa Foundation5 主题
-
Congruence-Similarity-And-Geometrical-Proof Aqa Foundation5 主题
-
Volume-And-Surface-Area Aqa Foundation3 主题
-
Circles-Arcs-And-Sectors Aqa Foundation3 主题
-
Area-And-Perimeter Aqa Foundation4 主题
-
Bearings-Scale-Drawing-Constructions-And-Loci Aqa Foundation5 主题
-
2D-And-3D-Shapes Aqa Foundation4 主题
-
Angles-In-Polygons-And-Parallel-Lines Aqa Foundation5 主题
-
Symmetry-And-Shapes Aqa Foundation4 主题
-
Exchange-Rates-And-Best-Buys Aqa Foundation2 主题
-
Standard-And-Compound-Units Aqa Foundation5 主题
-
Direct-And-Inverse-Proportion Aqa Foundation1 主题
-
Ratio-Problem-Solving Aqa Foundation2 主题
-
Sequences Aqa Foundation4 主题
-
Solving-Inequalities Aqa Foundation3 主题
-
Real-Life-Graphs Aqa Foundation4 主题
-
Graphs-Of-Functions Aqa Foundation3 主题
-
Linear-Graphs Aqa Foundation3 主题
-
Coordinate-Geometry Aqa Foundation3 主题
-
Functions Aqa Foundation1 主题
-
Forming-And-Solving-Equations Aqa Foundation2 主题
-
Simultaneous-Equations Aqa Foundation1 主题
-
Solving-Quadratic-Equations Aqa Foundation1 主题
-
Linear-Equations Aqa Foundation3 主题
-
Algebraic-Reasoning Aqa Foundation1 主题
-
Rearranging-Formulas Aqa Foundation1 主题
-
Introduction Aqa Foundation10 主题
-
Relative-And-Expected-Frequency Aqa Foundation
-
Sample-Space-Diagrams Aqa Foundation
-
Basic-Probability Aqa Foundation
-
Sharing-In-A-Ratio Aqa Foundation
-
Equivalent-And-Simplified-Ratios Aqa Foundation
-
Introduction-To-Ratios Aqa Foundation
-
Collecting-Like-Terms Aqa Foundation
-
Substitution Aqa Foundation
-
Algebraic-Vocabulary Aqa Foundation
-
Algebraic-Notation Aqa Foundation
-
Relative-And-Expected-Frequency Aqa Foundation
-
Factorising Aqa Foundation3 主题
-
Expanding-Brackets Aqa Foundation2 主题
-
Algebraic-Roots-And-Indices Aqa Foundation1 主题
-
Using-A-Calculator Aqa Foundation1 主题
-
Exact-Values Aqa Foundation1 主题
-
Rounding-Estimation-And-Error-Intervals Aqa Foundation4 主题
-
Fractions-Decimals-And-Percentages Aqa Foundation2 主题
-
Simple-And-Compound-Interest-Growth-And-Decay Aqa Foundation4 主题
-
Percentages Aqa Foundation5 主题
-
Fractions Aqa Foundation6 主题
-
Powers-Roots-And-Standard-Form Aqa Foundation4 主题
-
Types-Of-Number-Prime-Factors-Hcf-And-Lcm Aqa Foundation6 主题
-
Number-Operations Aqa Foundation9 主题
-
Counting-Principles Aqa Foundation
-
Related-Calculations Aqa Foundation
-
Multiplication-And-Division Aqa Foundation
-
Addition-And-Subtraction Aqa Foundation
-
Money-Calculations Aqa Foundation
-
Negative-Numbers Aqa Foundation
-
Place-Value Aqa Foundation
-
Order-Of-Operations-Bidmasbodmas Aqa Foundation
-
Mathematical-Operations Aqa Foundation
-
Counting-Principles Aqa Foundation
Planes-Of-Symmetry Aqa Foundation
Exam code:8300
Planes of symmetry
What is a plane of symmetry?
-
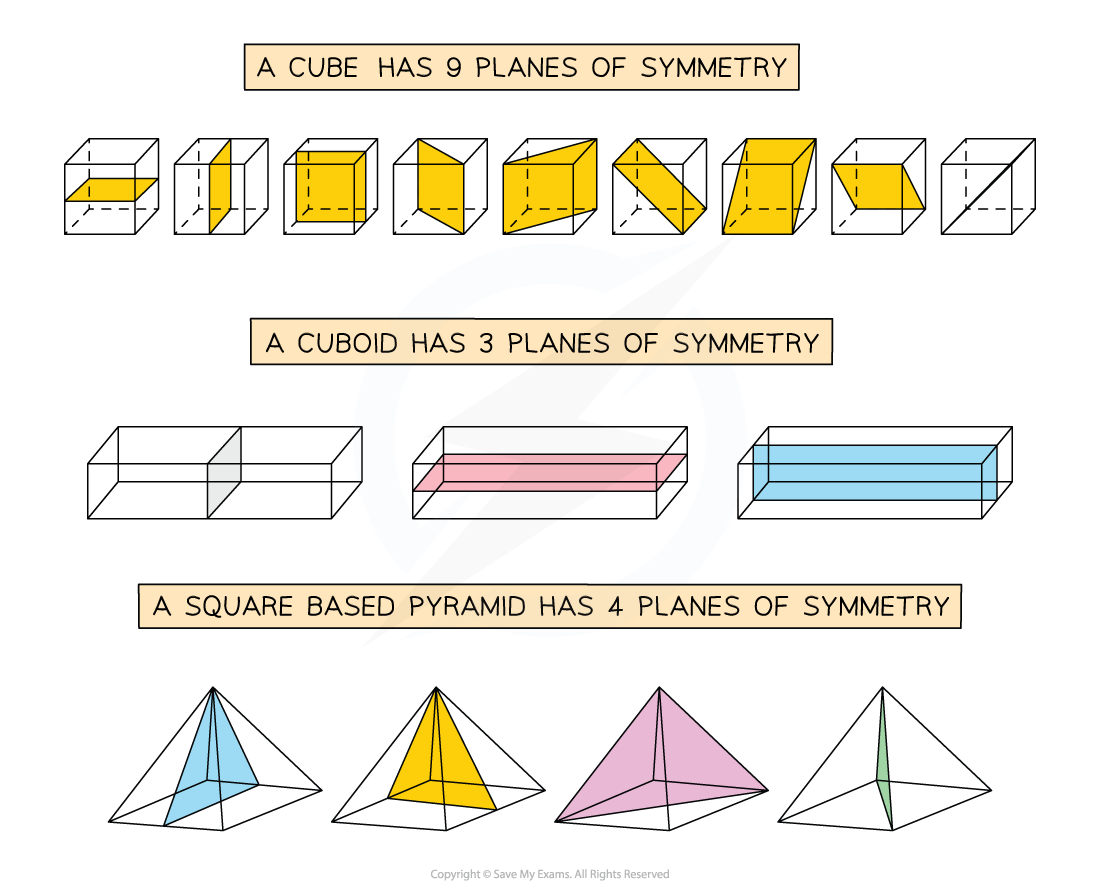
A plane is a flat surface that can be any 2D shape
-
A plane of symmetry is a plane that splits a 3D shape into two congruent (identical) halves
-
If a 3D shape has a plane of symmetry, it has reflection symmetry
-
The two congruent halves are identical, mirror images of each other
-
-
All prisms have at least one plane of symmetry
-
Cubes have 9 planes of symmetry
-
Cuboids have 3 planes of symmetry
-
Cylinders have an infinite number of planes of symmetry
-
The number of planes of symmetry in other prisms will be equal to the number of lines of symmetry in its cross-section plus 1
-
-
Pyramids can have planes of symmetry too
-
The number of planes of symmetry in pyramids will be equal to the number of lines of symmetry in its 2D base
-
If the base of the pyramid is a regular polygon of n sides, it will have n planes of symmetry
-
Can a 3D shape have rotational symmetry?
-
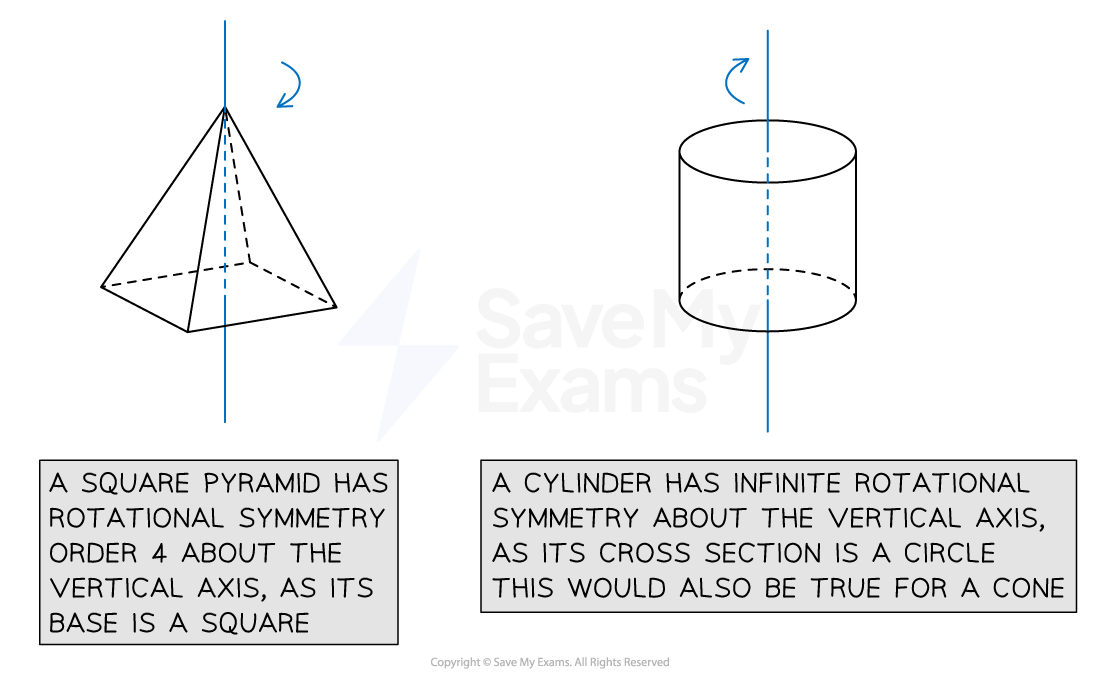
3D shapes are able to be rotated around different axes
-
Depending on which axis the shape is rotated around, 3D shapes can have rotational symmetry
-
-
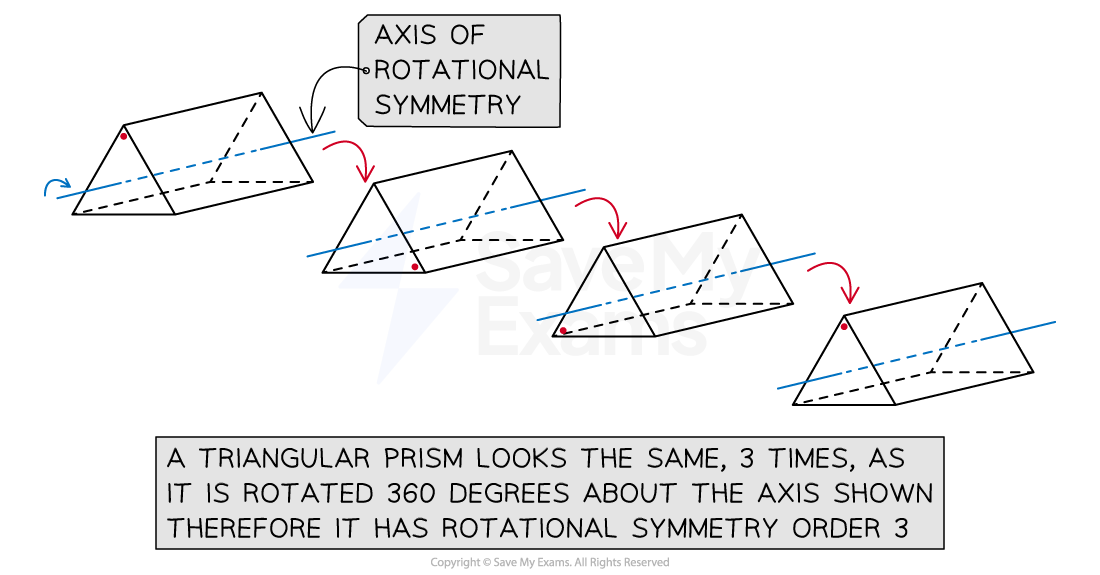
Recall that rotational symmetry is how many times the shape looks the same (congruent) when rotated through 360 degrees
-
See the example of the triangular prism where the cross-section is an equilateral triangle
-
Examiner Tips and Tricks
-
If you’re unsure in the exam, consider the properties of the 3D shape.
-
Is it a prism or a pyramid?
-
How many lines of symmetry are there in the 2D faces or cross-section?
-
Worked Example
The diagram below shows a cuboid of length 8 cm, width 5 cm and height 11 cm.
Write down the number of planes of symmetry of this cuboid.
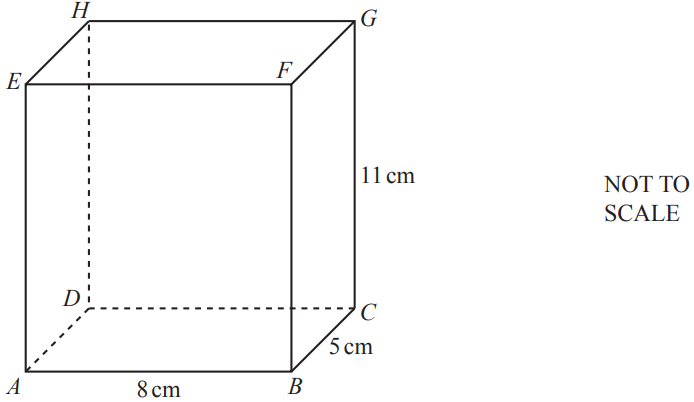
A plane of symmetry is where a shape can be “sliced” such that it is symmetrical
A cuboid with three different pairs of opposite rectangles has 3 planes of symmetry
3 planes of symmetry

Responses