Frequency-Trees Aqa Foundation

课 Progress

0% Complete

Exam code:8300

Frequency trees

What are frequency trees?

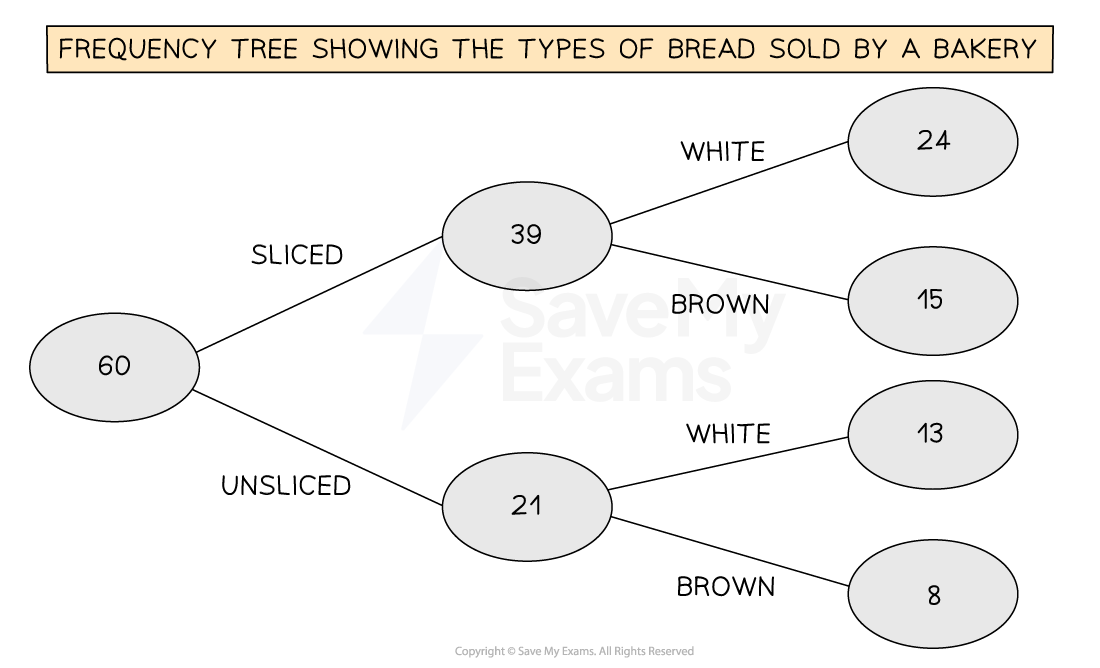
Frequency trees show the frequencies associated with two properties of a set of data
They are usually used when each property only has two possible outcomes
- For example the types of bread sold by a bakery in a day
  - The first property could be if the bread is sliced or unsliced
  - The second property could be if the bread is white or brown
- A frequency tree shows the frequency for each combination
  - e.g how many sliced, white loaves of bread were sold
The total frequency appears in a ‘bubble’ at the start of a frequency tree
- The first set of branches then break this down by the two outcomes for the first property
- The second set of branches then further breaks down each of those frequencies
It does not matter which set of branches shows which property
It is possible to have three, or more, properties on a frequency tree by adding more sets of branches
- However these would quickly become large and cumbersome
For situations with more than two options for a property, two-way tables are more useful
- For example if the bread in the bakery could brown, white, or seeded

Frequency tree showing the types of bread sold by a bakery, broken down first by sliced or unsliced, and then by brown or white

How do I draw a frequency tree?

If drawing a frequency tree from scratch
- Identify the two properties
- Decide which property to put on the first set of branches and which to put on the second set of branches
- Remember to include a ‘bubble’ at the start for the total frequency and a ‘bubble’ at the end of each branch
Double check that the values at the ends of the branches, sum to the ‘bubble’ that they are connected to

How do I complete a frequency tree?

Often in an exam there will be a partially completed frequency tree
Check for any values in the question that you can use to fill in gaps
- e.g. “A total of 100 people”
Remember that the values at the ends of the branches, sum to the ‘bubble’ that they are connected to
- This should allow you to fill in any gaps that aren’t revealed by the information in the question

How do I find probabilities from a frequency tree?

Similar to finding probabilities from two-way tables, you need to select the appropriate numbers from the diagram
It can help to rephrase the question to use AND & OR statements
- e.g. The probability of selecting a loaf of sliced white bread is P(“sliced AND white”)
Use the branches to help select the values you need to write down the probability
- For “sliced AND white” this would be the along the branch saying ‘sliced’ on the first property and ‘white’ on the second
  - The value in the bubble at the end of the required branch(es) would be the numerator
- The denominator will be the total of the group we are choosing from
  - This could be the whole group – the total frequency at the start of the diagram
  - Or if we are finding a probability from just sliced loaves, it would be the frequency in the bubble at the end of the ‘sliced’ branch
You may need to add together values
- e.g. To find the total number of white loaves of bread sold, sum together the sliced white loaves and the unsliced white loaves

Examiner Tips and Tricks

Double check that the values at the ends of the tree add up to the starting value
Some of the frequencies may be given as fractions or percentages of others
- e.g. 65% of the loaves of bread sold were sliced

Worked Example

80 students are learning how to DJ. There are two courses; scratch mixing, and beat mixing.
60% of the students are studying scratch mixing, the rest are studying beat mixing.
Of those studying scratch mixing, 15 are female.
Of those studying beat mixing, 12 are male.

(a) Use the information above to complete the frequency tree.

Start with the total frequency bubble at the start of the frequency tree – 80.
Work out 60% of 80 to find the frequency for scratch mixing.

$table row cell 10 percent sign space of space 80 space end cell equals cell 80 divided by 10 equals 8 end cell row cell 60 percent sign space of space 80 space end cell equals cell space 8 cross times 6 equals 48 end cell end table$

Work your way through the rest of the tree.

beat: <img alt=”80 space minus space 48 space equals 32″ data-mathml='<math ><semantics><mrow><mn>80</mn><mo> </mo><mo>-</mo><mo> </mo><mn>48</mn><mo> </mo><mo>=</mo><mn>32</mn></mrow><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true}</annotation></semantics></math>’ data-type=”working” height=”22″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2222%22%20width%3D%22101%22%20wrs%3Abaseline%3D%2216%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmn%20mathcolor%3D%22%23000%22%3E80%3C%2Fmn%3E%3Cmo%20mathcolor%3D%22%23000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000%22%3E-%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmn%20mathcolor%3D%22%23000%22%3E48%3C%2Fmn%3E%3Cmo%20mathcolor%3D%22%23000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%20mathcolor%3D%22%23000%22%3E%3D%3C%2Fmo%3E%3Cmn%20mathcolor%3D%22%23000%22%3E32%3C%2Fmn%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math135b31cfba37a56451b4768509d’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAAA%2FGhlYWQQC2qxAAACkAAAADZoaGVhCGsXSAAAAsgAAAAkaG10eE2rRkcAAALsAAAADGxvY2EAHTwYAAAC%2BAAAABBtYXhwBT0FPgAAAwgAAAAgbmFtZaBxlY4AAAMoAAABn3Bvc3QB9wD6AAAEyAAAACBwcmVwa1uragAABOgAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0iEv%2F%2FAAAAPSIS%2F%2F%2F%2FxN3wAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAEAgAFVAtUBqwADADAYAbAEELEAA%2FawAzyxAgf1sAE8sQUD5gCxAAATELEABuWxAAETELABPLEDBfWwAjwTIRUhgAJV%2FasBq1YAAQAAAAEAANV4zkFfDzz1AAMEAP%2F%2F%2F%2F%2FWOhNz%2F%2F%2F%2F%2F9Y6E3MAAP8gBIADqwAAAAoAAgABAAAAAAABAAAD6P9qAAAXcAAA%2F7YEgAABAAAAAAAAAAAAAAAAAAAAAwNSAFUDVgCAA1YAgAAAAAAAAAAoAAAAsgAAAPwAAQAAAAMAXgAFAAAAAAACAIAEAAAAAAAEAADeAAAAAAAAABUBAgAAAAAAAAABABIAAAAAAAAAAAACAA4AEgAAAAAAAAADADAAIAAAAAAAAAAEABIAUAAAAAAAAAAFABYAYgAAAAAAAAAGAAkAeAAAAAAAAAAIABwAgQABAAAAAAABABIAAAABAAAAAAACAA4AEgABAAAAAAADADAAIAABAAAAAAAEABIAUAABAAAAAAAFABYAYgABAAAAAAAGAAkAeAABAAAAAAAIABwAgQADAAEECQABABIAAAADAAEECQACAA4AEgADAAEECQADADAAIAADAAEECQAEABIAUAADAAEECQAFABYAYgADAAEECQAGAAkAeAADAAEECQAIABwAgQBNAGEAdABoACAARgBvAG4AdABSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAE0AYQB0AGgAIABGAG8AbgB0AE0AYQB0AGgAIABGAG8AbgB0AFYAZQByAHMAaQBvAG4AIAAxAC4AME1hdGhfRm9udABNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAMAAAAAAAAB9AD6AAAAAAAAAAAAAAAAAAAAAAAAAAC5BxEAAI2FGACyAAAAFRQTsQABPw%3D%3D)format(‘truetype’)%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20fill%3D%22%23000%22%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2216%22%3E80%3C%2Ftext%3E%3Ctext%20fill%3D%22%23000%22%20font-family%3D%22math135b31cfba37a56451b4768509d%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2230.5%22%20y%3D%2216%22%3E%26%23×2212%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%23000%22%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2252.5%22%20y%3D%2216%22%3E48%3C%2Ftext%3E%3Ctext%20fill%3D%22%23000%22%20font-family%3D%22math135b31cfba37a56451b4768509d%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2273.5%22%20y%3D%2216%22%3E%3D%3C%2Ftext%3E%3Ctext%20fill%3D%22%23000%22%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle

Maths Gcse Aqa Foundation