Maths Gcse Edexcel Higher
-
Scatter-Graphs-And-Correlation Edexcel Higher2 主题
-
Cumulative-Frequency-And-Box-Plots Edexcel Higher4 主题
-
Histograms Edexcel Higher3 主题
-
Statistical-Diagrams Edexcel Higher7 主题
-
Averages-Ranges-And-Data Edexcel Higher8 主题
-
Capture-Recapture Edexcel Higher
-
Population-And-Sampling Edexcel Higher
-
Comparing-Data-Sets Edexcel Higher
-
Range-And-Interquartile-Range Edexcel Higher
-
Averages-From-Grouped-Data Edexcel Higher
-
Averages-From-Tables Edexcel Higher
-
Calculations-With-The-Mean Edexcel Higher
-
Mean-Median-And-Mode Edexcel Higher
-
Capture-Recapture Edexcel Higher
-
Combined-And-Conditional-Probability Edexcel Higher3 主题
-
Tree-Diagrams Edexcel Higher1 主题
-
Simple-Probability-Diagrams Edexcel Higher3 主题
-
Transformations Edexcel Higher5 主题
-
Vectors Edexcel Higher6 主题
-
3D-Pythagoras-And-Trigonometry Edexcel Higher1 主题
-
Sine-Cosine-Rule-And-Area-Of-Triangles Edexcel Higher4 主题
-
Pythagoras-And-Trigonometry Edexcel Higher4 主题
-
Area-And-Volume-Of-Similar-Shapes Edexcel Higher1 主题
-
Congruence-Similarity-And-Geometrical-Proof Edexcel Higher5 主题
-
Volume-And-Surface-Area Edexcel Higher3 主题
-
Circles-Arcs-And-Sectors Edexcel Higher2 主题
-
Area-And-Perimeter Edexcel Higher4 主题
-
Circle-Theorems Edexcel Higher7 主题
-
Circle-Theorem-Proofs Edexcel Higher
-
The-Alternate-Segment-Theorem Edexcel Higher
-
Angles-In-The-Same-Segment Edexcel Higher
-
Angles-In-Cyclic-Quadrilaterals Edexcel Higher
-
Theorems-With-Chords-And-Tangents Edexcel Higher
-
Angle-In-A-Semicircle Edexcel Higher
-
Angles-At-Centre-And-Circumference Edexcel Higher
-
Circle-Theorem-Proofs Edexcel Higher
-
Bearings-Scale-Drawing-Constructions-And-Loci Edexcel Higher5 主题
-
Angles-In-Polygons-And-Parallel-Lines Edexcel Higher3 主题
-
Symmetry-And-Shapes Edexcel Higher6 主题
-
Exchange-Rates-And-Best-Buys Edexcel Higher2 主题
-
Standard-And-Compound-Units Edexcel Higher5 主题
-
Direct-And-Inverse-Proportion Edexcel Higher2 主题
-
Problem-Solving-With-Ratios Edexcel Higher2 主题
-
Ratios Edexcel Higher3 主题
-
Sequences Edexcel Higher4 主题
-
Transformations-Of-Graphs Edexcel Higher2 主题
-
Graphing-Inequalities Edexcel Higher2 主题
-
Solving-Inequalities Edexcel Higher2 主题
-
Real-Life-Graphs Edexcel Higher4 主题
-
Estimating-Gradients-And-Areas-Under-Graphs Edexcel Higher2 主题
-
Equation-Of-A-Circle Edexcel Higher2 主题
-
Graphs-Of-Functions Edexcel Higher6 主题
-
Linear-Graphs Edexcel Higher4 主题
-
Coordinate-Geometry Edexcel Higher4 主题
-
Functions Edexcel Higher3 主题
-
Forming-And-Solving-Equations Edexcel Higher3 主题
-
Iteration Edexcel Higher1 主题
-
Simultaneous-Equations Edexcel Higher2 主题
-
Quadratic-Equations Edexcel Higher4 主题
-
Linear-Equations Edexcel Higher1 主题
-
Algebraic-Proof Edexcel Higher1 主题
-
Rearranging-Formulas Edexcel Higher2 主题
-
Algebraic-Fractions Edexcel Higher4 主题
-
Completing-The-Square Edexcel Higher1 主题
-
Factorising Edexcel Higher6 主题
-
Expanding-Brackets Edexcel Higher3 主题
-
Algebraic-Roots-And-Indices Edexcel Higher1 主题
-
Introduction Edexcel Higher7 主题
-
Using-A-Calculator Edexcel Higher1 主题
-
Surds Edexcel Higher2 主题
-
Rounding-Estimation-And-Bounds Edexcel Higher2 主题
-
Fractions-Decimals-And-Percentages Edexcel Higher3 主题
-
Simple-And-Compound-Interest-Growth-And-Decay Edexcel Higher4 主题
-
Percentages Edexcel Higher3 主题
-
Fractions Edexcel Higher4 主题
-
Powers-Roots-And-Standard-Form Edexcel Higher4 主题
-
Prime-Factors-Hcf-And-Lcm Edexcel Higher4 主题
-
Number-Operations Edexcel Higher10 主题
-
Product-Rule-For-Counting Edexcel Higher
-
Systematic-Lists Edexcel Higher
-
Related-Calculations Edexcel Higher
-
Multiplication-And-Division Edexcel Higher
-
Addition-And-Subtraction Edexcel Higher
-
Money-Calculations Edexcel Higher
-
Negative-Numbers Edexcel Higher
-
Irrational-Numbers Edexcel Higher
-
Order-Of-Operations-Bidmas-Bodmas Edexcel Higher
-
Mathematical-Symbols Edexcel Higher
-
Product-Rule-For-Counting Edexcel Higher
Constructions Edexcel Higher
Exam code:1MA1
Constructions
What are constructions?
-
A construction is a process where you create an accurate geometric object using a pair of compasses and a straight edge (and a pencil)
-
There are several types of construction you must be able to carry out:
-
A perpendicular bisector of a line
-
This is a line that cuts another one exactly in half (bisects) but also crosses it at a right angle (perpendicular)
-
It shows a path that is equidistant (equal distance) between the two endpoints of the line
-
-
A perpendicular from a point to a line
-
This is the shortest path between the point and the line
-
It will meet the line at a right angle
-
-
An angle bisector
-
This is a line that cuts an angle exactly in half (bisects)
-
It shows a path that is equidistant (equal distance) between the two lines that form the angle
-
-
How do I construct a perpendicular bisector of a line?
-
STEP 1
Set the distance between the point of the compasses and the pencil to be more than half the length of the line -
STEP 2
Place the point of the compasses on one end of the line and sketch an arc above and below the line -
STEP 3
Keeping your compasses set to the same distance, place the point of the compasses on the other end of the line and sketch an arc above and below the line-
The arcs should intersect each other both above and below the line
-
-
STEP 4
Connect the points where the arcs intersect with a straight line

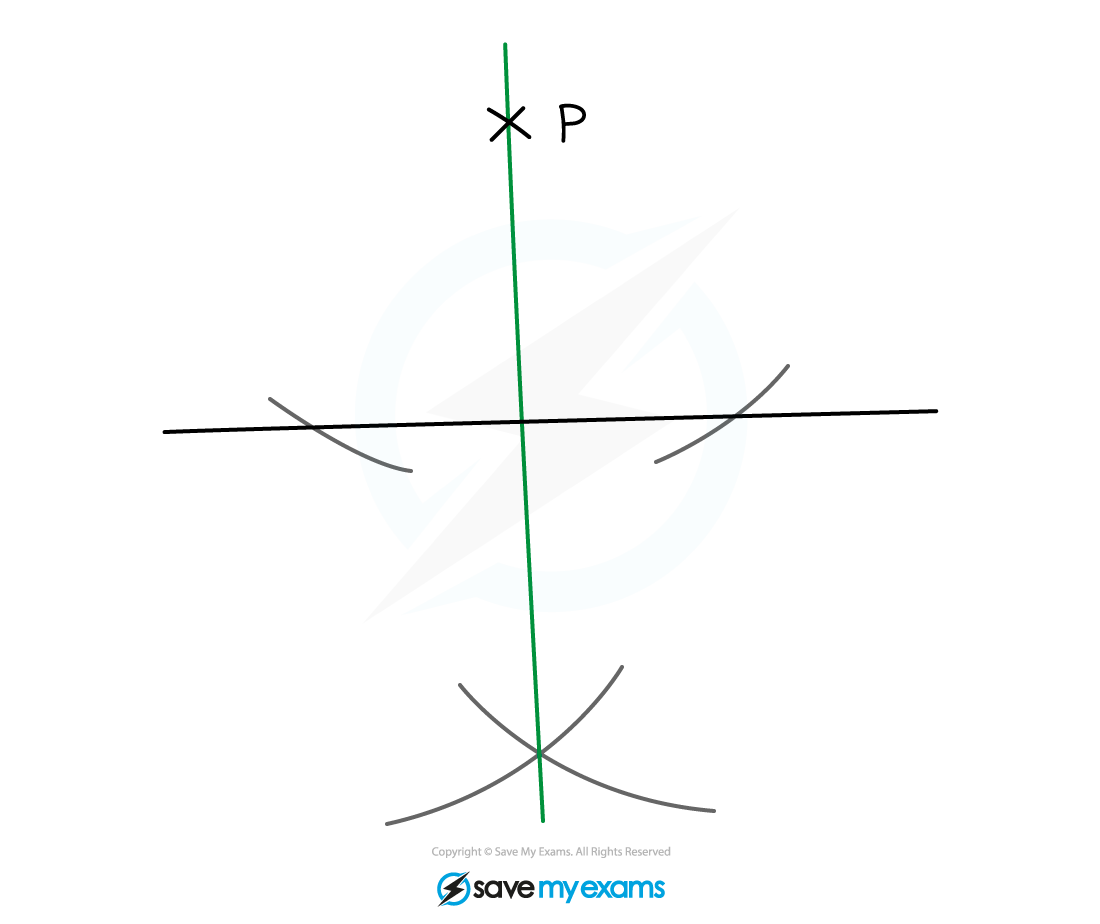
How do I construct a perpendicular from a point to a line?
-
STEP 1
Set the distance between the point of your compasses and the pencil to be greater than the distance between the point P and the line -
STEP 2
Placing the point of the compasses on the point P, draw an arc that intersects the line in two places -
STEP 3
Set the distance between the point of the compasses and the pencil to be more than half the distance between the two points of intersection on the line -
STEP 4
Place the point of the compasses on one point of intersection and sketch an arc on the opposite side of the line to P -
STEP 5
Keeping your compasses set to the same distance, place the point of the compasses on the other point of intersection and sketch an another arc-
The arcs should intersect
-
-
STEP 6
Connect the point where the arcs intersect to point P with a straight line
How do I construct an angle bisector?
-
STEP 1
Set the distance between the point of your compasses and the pencil to be about half the distance of the smallest line that makes the angle-
The precise distance is not important
-
-
STEP 2
Place the point of the compasses where the lines meet and sketch an arc that intersects both of the lines that form the angle -
STEP 3
Keeping your compasses set to the same distance, place the point of the compasses on one of the points of intersection and sketch an arc -
STEP 4
Keeping your compasses set to the same distance, place the point of the compasses on the other point of intersection and sketch an arc-
This should intersect the last arc you drew
-
-
STEP 5
Join the point of the angle to the point of intersection with a straight line

Examiner Tips and Tricks
-
Make sure you have all the equipment you need for the exam; pen, pencil, ruler, compasses, protractor, calculator
-
An eraser and a pencil sharpener can be helpful on these questions as they are all about accuracy
-
But do not erase your construction lines
-
-
Make sure your compasses aren’t loose and wobbly
-
They can usually be tightened with a screwdriver
-
-
Make sure you can see and read the markings on your ruler and protractor

Responses