Similar-Lengths Edexcel Higher

课 Progress

0% Complete

Exam code:1MA1

Similar lengths

How do I find the scale factor between lengths on similar shapes?

Equivalent lengths on two similar shapes will be in the same ratio and are linked by a scale factor
Establish the type of enlargement
- If the second shape is bigger
  - then the scale factor is greater than 1
- If the second shape is smaller
  - then the scale factor is greater than 0 but less than 1
To find the scale factor
- Identify known lengths of corresponding sides
- Divide the length on the second shape by the corresponding length on the first shape

How do I find missing lengths on similar shapes?

Method 1

STEP 1
Find the scale factor to get from the first shape to the second shape
- Divide a length on the second by the corresponding length on the first
- The scale factor can be less than 1 for this method
STEP 2
Use the scale factor to find the length you need
- To find a missing length on the second shape
  - Multiply the corresponding length on the first shape by the scale factor
- To find a missing length on the first shape
  - Divide the corresponding length on the first shape by the scale factor

Method 2

STEP 1
Find the scale factor to get from the smaller shape to the bigger shape
- Divide a length on the bigger shape by the corresponding length on the smaller shape
- The scale factor is always greater than 1 for this method
STEP 2
Use the scale factor to find the length you need
- To find a missing length on the bigger shape
  - Multiply the corresponding length on the smaller shape by the scale factor
- To find a missing length on the smaller shape
  - Divide the corresponding length on the bigger shape by the scale factor

Examiner Tips and Tricks

If similar shapes overlap on the diagram (or are not clear) draw them separately.

For example, in this diagram the triangles ABC and APQ are similar:

So redraw them separately before starting:

Worked Example

ABCD and PQRS are similar shapes.
Find the length of PS.

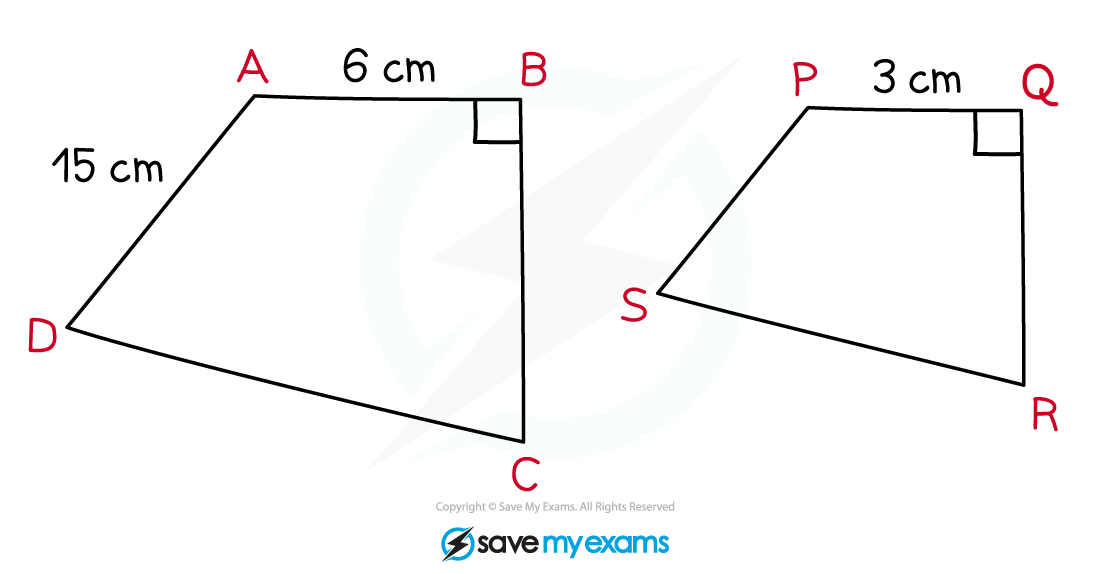
The two shapes are mathematically similar

Identify two known corresponding sides of the similar shapes

AB and PQ are corresponding sides

Method 1

The second shape is smaller than the first shape so the scale factor will be between 0 and 1
Divide the known length on the second shape by the corresponding length on the first shape to find the scale factor

$table row cell Scale space Factor space end cell equals cell 3 over 6 equals 1 half end cell end table$

Multiply the length AD by the scale factor to find its corresponding length PS on the second shape

<img alt=”table attributes columnalign right center left columnspacing 0px end attributes row cell P S space end cell equals cell 1 half cross times 15 equals 15 over 2 end cell row blank blank blank end table” data-mathml='<math ><semantics><mtable columnspacing=”0px” columnalign=”right center left”><mtr><mtd><mi >P</mi><mi >S</mi><mo > </mo></mtd><mtd><mo >=</mo></mtd><mtd><mfrac ><mn>1</mn><mn>2</mn></mfrac><mo >×</mo><mn >15</mn><mo >=</mo><mfrac ><mn>15</mn><mn>2</mn></mfrac></mtd></mtr><mtr><mtd></mtd><mtd></mtd><mtd></mtd></mtr></mtable><annotation encoding=”application/vnd.wiris.mtweb-params+json”>{“language”:”en”,”fontFamily”:”Times New Roman”,”fontSize”:”18″,”autoformat”:true}</annotation></semantics></math>’ data-type=”working” height=”73″ role=”math” src=”data:image/svg+xml;charset=utf8,%3Csvg%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20xmlns%3Awrs%3D%22http%3A%2F%2Fwww.wiris.com%2Fxml%2Fmathml-extension%22%20height%3D%2273%22%20width%3D%22138%22%20wrs%3Abaseline%3D%2236%22%3E%3C!–MathML%3A%20%3Cmath%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F1998%2FMath%2FMathML%22%3E%3Cmtable%20columnalign%3D%22right%20center%20left%22%20columnspacing%3D%220px%22%3E%3Cmtr%3E%3Cmtd%3E%3Cmi%20mathcolor%3D%22%23000000%22%3EP%3C%2Fmi%3E%3Cmi%20mathcolor%3D%22%23000000%22%3ES%3C%2Fmi%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23xA0%3B%3C%2Fmo%3E%3C%2Fmtd%3E%3Cmtd%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%3D%3C%2Fmo%3E%3C%2Fmtd%3E%3Cmtd%3E%3Cmfrac%20mathcolor%3D%22%23000000%22%3E%3Cmn%3E1%3C%2Fmn%3E%3Cmn%3E2%3C%2Fmn%3E%3C%2Fmfrac%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%26%23xD7%3B%3C%2Fmo%3E%3Cmn%20mathcolor%3D%22%23000000%22%3E15%3C%2Fmn%3E%3Cmo%20mathcolor%3D%22%23000000%22%3E%3D%3C%2Fmo%3E%3Cmfrac%20mathcolor%3D%22%23000000%22%3E%3Cmn%3E15%3C%2Fmn%3E%3Cmn%3E2%3C%2Fmn%3E%3C%2Fmfrac%3E%3C%2Fmtd%3E%3C%2Fmtr%3E%3Cmtr%3E%3Cmtd%2F%3E%3Cmtd%2F%3E%3Cmtd%2F%3E%3C%2Fmtr%3E%3C%2Fmtable%3E%3C%2Fmath%3E–%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A’math102a87acd26f5771b4d57a7dfb3’%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAABIWhlYWQQC2qxAAACuAAAADZoaGVhCGsXSAAAAvAAAAAkaG10eE2rRkcAAAMUAAAADGxvY2EAHTwYAAADIAAAABBtYXhwBT0FPgAAAzAAAAAgbmFtZaBxlY4AAANQAAABn3Bvc3QB9wD6AAAE8AAAACBwcmVwa1uragAABRAAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0A1%2F%2F%2FAAAAPQDX%2F%2F%2F%2FxP8rAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAIAgABVAtUCgAADAAcARhiwARQAsQAAExCxAAnksQABExCwBDyxBgj0sAI8MAGxCAETELEAA%2FawBzyxAQX1sAY8sgUHABD0sAI8sQkD5rEEBfWwAzwTMwEjETMBI4BVAgBVVf4AVQKA%2FdUCK%2F3VAAAAAAEAAAABAADVeM5BXw889QADBAD%2F%2F%2F%2F%2F1joTc%2F%2F%2F%2F%2F%2FWOhNzAAD%2FIASAA6sAAAAKAAIAAQAAAAAAAQAAA%2Bj%2FagAAF3AAAP%2B2BIAAAQAAAAAAAAAAAAAAAAAAAAMDUgBVA1YAgANWAIAAAAAAAAAA

Maths Gcse Edexcel Higher