Similarity Edexcel Foundation

课 Progress

0% Complete

Exam code:1MA1

Similarity

What are similar shapes?

Two shapes are similar if they have the same shape and their corresponding sides are in proportion
- One shape is an enlargement of the other

How do we prove that two triangles are similar?

To show that two triangles are similar you need to show that their angles are the same
- If the angles are the same then corresponding lengths of a triangle will automatically be in proportion
You can use angle properties to identify equal angles
- Look out for for isosceles triangles, vertically opposite angles and angles on parallel lines
If a question asks you to prove two triangles are similar
- For each pair of corresponding angles
  - State that they are of equal size
  - Give a reason for why they are equal

How do we prove that two shapes are similar?

To show that two non-triangular shapes are similar you need to show that their corresponding sides are in proportion
- Divide the length of one side by the length of the corresponding side on the other shape to find the scale factor
If the scale factor is the same for all corresponding sides, then the shapes are similar

Examiner Tips and Tricks

A pair of similar triangles can often be opposite each other in an hourglass formation.
- Look out for the vertically opposite, equal angles.
- It may be helpful to sketch the triangles next to each other and facing in the same direction.

Worked Example

(a) Prove that the two rectangles shown in the diagram below are similar.

Use the corresponding lengths (15 cm and 6 cm) to find the scale factor

$15 over 6 space equals space 2.5$

Use the corresponding width (5 cm and 2 cm) to find the scale factor for the other pair of sides

$5 over 2 equals 2.5$

The two rectangles are similar, with a scale factor of 2.5

(b) In the diagram below, AB and CD are parallel lines.
Show that triangles ABX and CDX are similar.

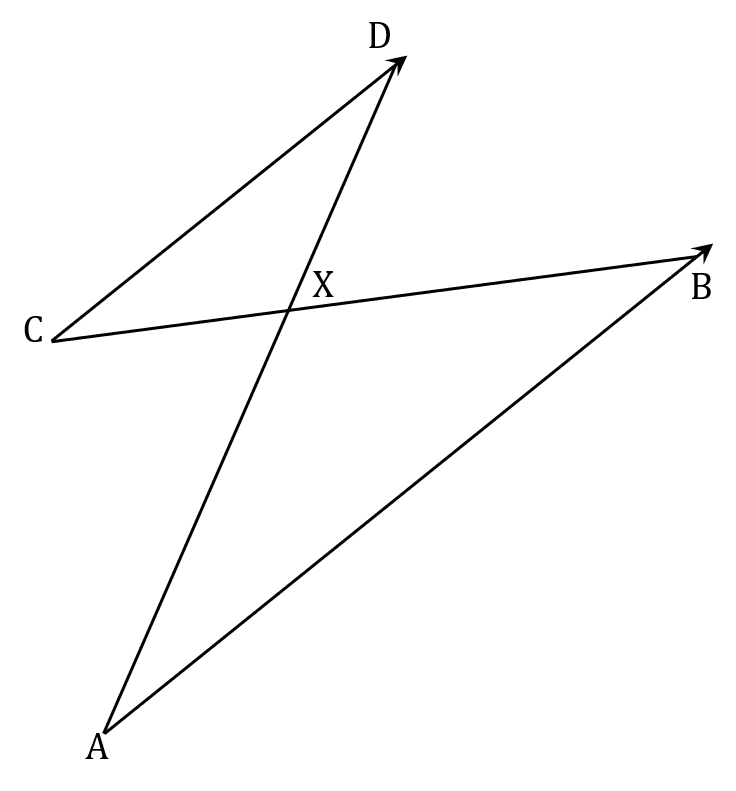
State the equal angles by name, along with clear reasons
Don’t forget to state that similar triangles need to have equal corresponding angles

Angle AXB = angle CXD (vertically opposite angles are equal)
Angle ABC = angle BCD (alternate angles on parallel lines are equal)
Angle BAD = angle ADC (alternate angles on parallel lines are equal)

All three corresponding angles are equal, so the two triangles are similar

Maths Gcse Edexcel Foundation