Computer Science GCES EDEXCEL
-
Decomposition And Abstraction Edexcel2 主题
-
Algorithms Edexcel11 主题
-
Follow And Write Algorithms Edexcel
-
Introduction To Programming Concepts Edexcel
-
Basic Programming Concepts Edexcel
-
Variables Constants And Assignments Edexcel
-
Data Structures And Arrays Edexcel
-
Arithmetic Relational And Logical Operations Edexcel
-
Determine Outputs Of An Algorithm Edexcel
-
Types Of Errors Edexcel
-
Standard Sorting Algorithms Edexcel
-
Standard Searching Algorithms Edexcel
-
Algorithm Efficiency Edexcel
-
Follow And Write Algorithms Edexcel
-
Truth Tables Edexcel3 主题
-
Binary Edexcel6 主题
-
Data Representation Edexcel4 主题
-
Data Storage And Compression Edexcel2 主题
-
Hardware Edexcel5 主题
-
Software Edexcel3 主题
-
Programming Languages Edexcel2 主题
-
Networks Edexcel7 主题
-
Network Security Edexcel2 主题
-
Environmental Issues Edexcel1 主题
-
Ethical And Legal Issues Edexcel3 主题
-
Cybersecurity Edexcel2 主题
-
Develop Code Edexcel6 主题
-
Constructs Edexcel4 主题
-
Data Types And Data Structures Edexcel5 主题
-
Operators Edexcel1 主题
-
Subprograms Edexcel2 主题
Converting Between Hexadecimal And Binary Edexcel
Exam code:1CP2
The Use of Hexadecimal in Computing
Why is hexadecimal used?
-
In Computer Science hexadecimal is often preferred when working with large values
-
It takes fewer digits to represent a given value in hexadecimal than in binary
-
1 hexadecimal digit corresponds 4 bits (one nibble) and can represent 16 unique values (0-F)
-
-
It is beneficial to use hexadecimal over binary because:
-
The more bits there are in a binary number, the harder it makes for a human to read
-
Numbers with more bits are more prone to errors when being copied
-
-
Examples of where hexadecimal can be seen:
-
MAC addresses
-
Colour values
-
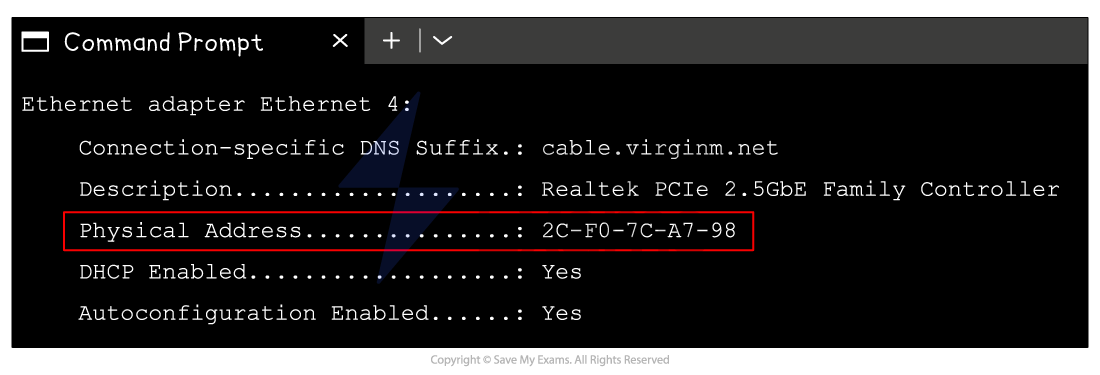
-
A typical MAC address consists of 12 hexadecimal digits, equivalent to 48 digits in in binary
-
AA:BB:CC:DD:EE:FF
-
10101010:10111011:11001100:11011101:11101110:11111111
-
-
Writing down or performing calculations with 48 binary digits makes it very easy to make a mistake
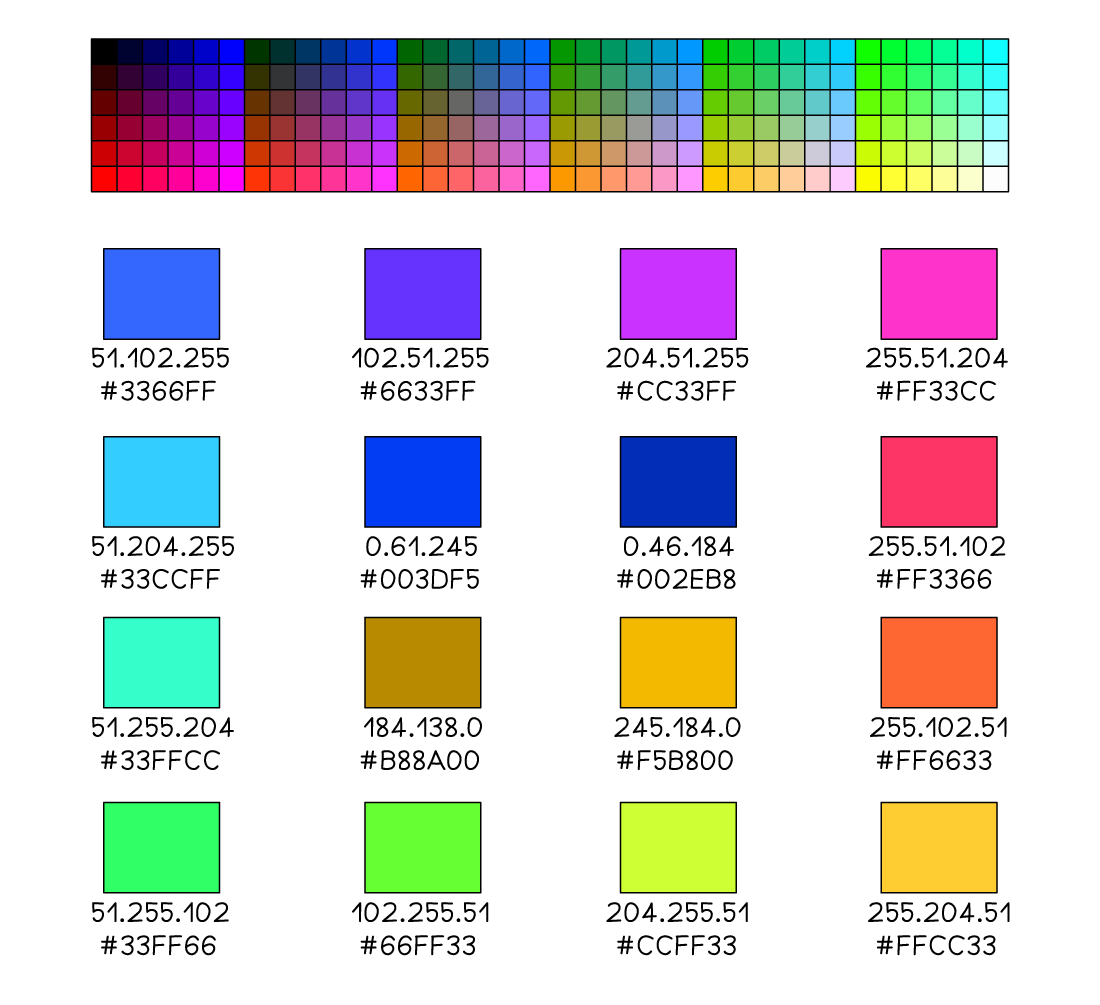
-
A typical hexadecimal colour code consists of 6 hexadecimal digits, equivalent to 24 digits in binary
-
#66FF33 (green)
-
01000010:11111111:00110011
-
Hexadecimal to Binary Conversion
How do you convert from hexadecimal to binary?
Example 1
-
To convert the hexadecimal number 5F to binary, first split the digits apart and convert each to a binary nibble (4 bits)
|
8 |
4 |
2 |
1 |
|
|---|---|---|---|---|
|
0 |
1 |
0 |
1 |
= 5 |
|
8 |
4 |
2 |
1 |
|
|---|---|---|---|---|
|
1 |
1 |
1 |
1 |
= 15 (F) |
-
Join the 2 binary nibbles together to create an 8 bit binary number
|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|---|---|---|---|---|---|---|---|
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
-
Hexadecimal 5F is 01011111 in binary
Example 2
-
To convert the hexadecimal number 26 to binary, first split the digits apart and convert each to a binary nibble (4 bits)
|
8 |
4 |
2 |
1 |
|
|---|---|---|---|---|
|
0 |
0 |
1 |
0 |
= 2 |
|
8 |
4 |
2 |
1 |
|
|---|---|---|---|---|
|
0 |
1 |
1 |
0 |
= 6 |
-
Join the 2 binary nibbles together to create an 8 bit binary number
|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|---|---|---|---|---|---|---|---|
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
-
Hexadecimal 26 is 00100110 in binary
Binary to Hexadecimal Conversion
How do you convert from binary to hexadecimal?
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
Example 1
-
To convert the binary number 10110111 to hexadecimal, first split the 8 bit number into 2 binary nibbles
|
8 |
4 |
2 |
1 |
|
8 |
4 |
2 |
1 |
|---|---|---|---|---|---|---|---|---|
|
1 |
0 |
1 |
1 |
|
0 |
1 |

Responses