bubble-sort

Bubble Sort

What is a bubble sort?

• A bubble sort sorts items into order, smallest to largest

• It compares pairs of elements and swaps them if they are out of order

• The first element is compared to the second, the second to the third, the third to the fourth and so on, until the second to last is compared to the last. Swaps occur if each comparison is out of order

• This overall process is called a pass

• Once the end of the list has been reached, the value at the top of the list is now in order and the sort resets back to the start of the list. The next largest value is then sorted to the top of the list

• More passes are completed until all elements are in the correct order

• A final pass checks all elements and if no swaps are made then the sort is complete

• An example of using a bubble sort would be sorting an array of names into alphabetical order, or sorting an array of student marks from a test

Performing the bubble sort

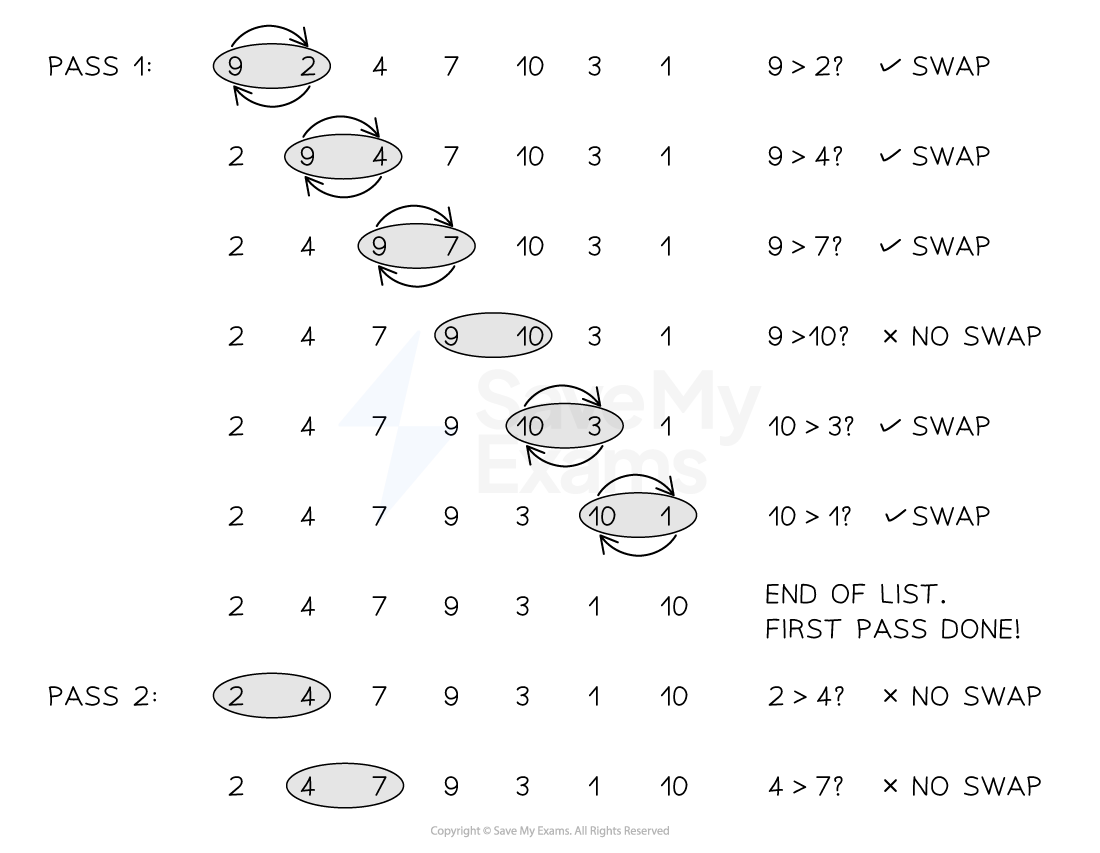
Figure 1: Performing the Bubble sort

Time complexity of the bubble sort

• To determine the algorithm’s execution time as measured by the number of instructions or steps carried out Big-O notation must be used

• Four statements are present in the above algorithm O(1), followed by a while loop O(n) containing two statements and a further for loop O(n). This results in the expression: 2n² + 4

• As coefficients and lower order values are not used, this give the bubble sort O(n²) worst case time complexity

• The best case scenario would be an already sorted list which means a time complexity of O(n) as each item must still be compared to check if they are in order

• The average case scenario would be an almost sorted list leading to O(n²/2), which if coefficients are removed still gives O(n²)

Space complexity of the bubble sort

• A bubble sort has a space complexity of O(1) because it operates in-place, requiring a fixed amount of memory

• The fixed amount of memory is for variables such as loop counters and a temporary swap variable

Tracing a bubble sort

• The trace table follows the algorithm through, updating values that change in the table

• Each iteration of the list reduces the overall size of the list by 1 as after each pass the previously sorted final digit is in order and does not need to be rechecked. This means that 9 is in order and doesn’t need to be rechecked, followed by 9 and 7, followed by 9, 7 and 6 and so on

• When the if statement is checked a new row has been added to show the swap of list[j], list[j + 1] and Temp, followed by the subsequent change to Swap from FALSE to TRUE

• After several iterations (that are not shown) the algorithm will eventually output a sorted list

Trace table of the bubble sort

Implementing a Bubble Sort

Pseudocode

list = [5, 9, 4, 2, 6, 7, 1, 2, 4, 3]
last = len(list)
swap = True
i = 0
while i < (last - 1) and (swap = True) swap = False for j = 0 to last - i - 2 if list[j] > list[j+1] temp = list[j] list[j] = list[j+1] list[j+1] = temp swap = True endif next j i = i + 1
endwhile
print(list)