quick-sort

Quick sort

What is a quick sort?

• A quick sort is another example of a divide and conquer algorithm that reduces the size of the problem into smaller problems that are more easily solvable by an algorithm

• Below is an illustration of the quick sort

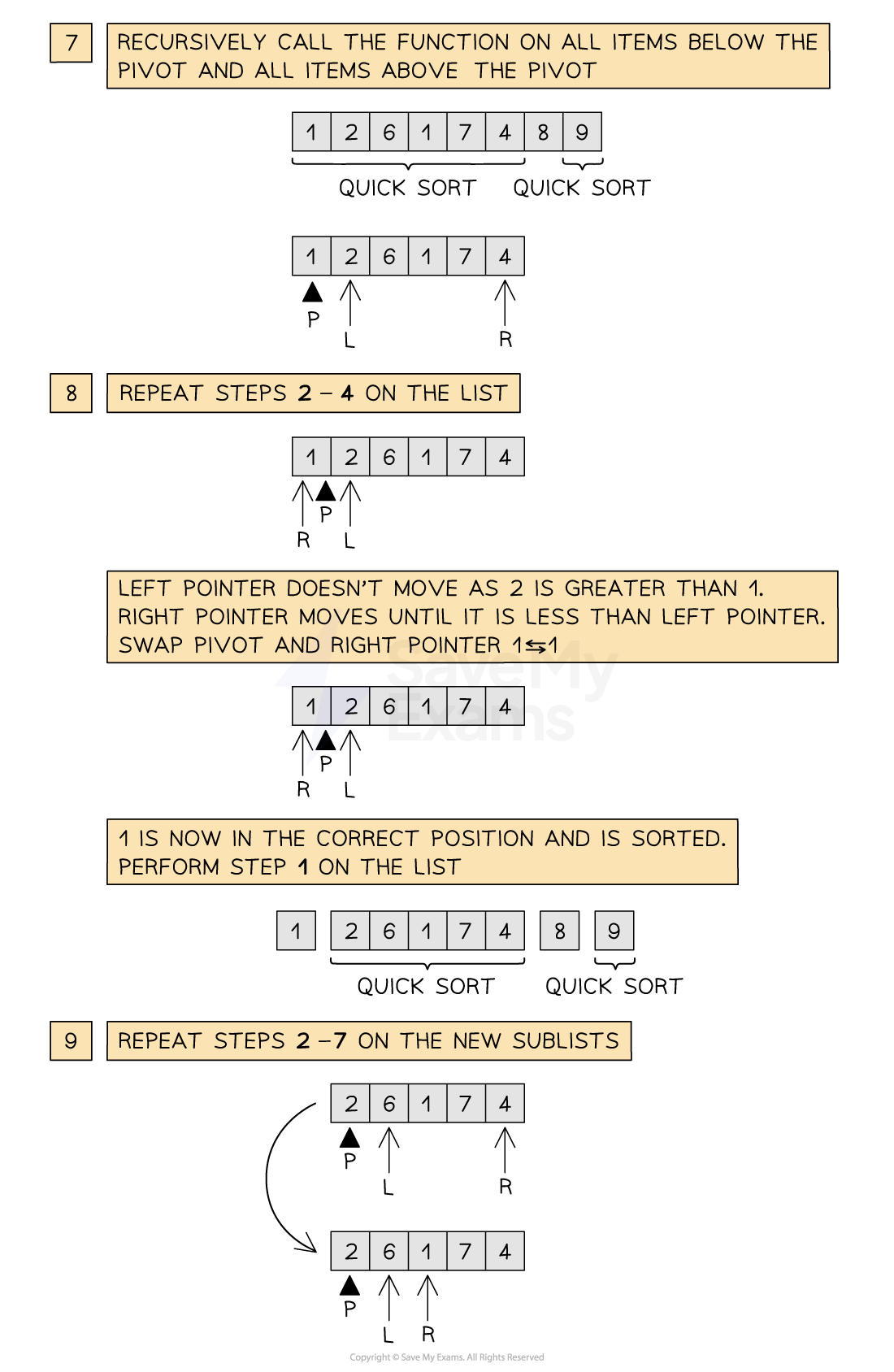
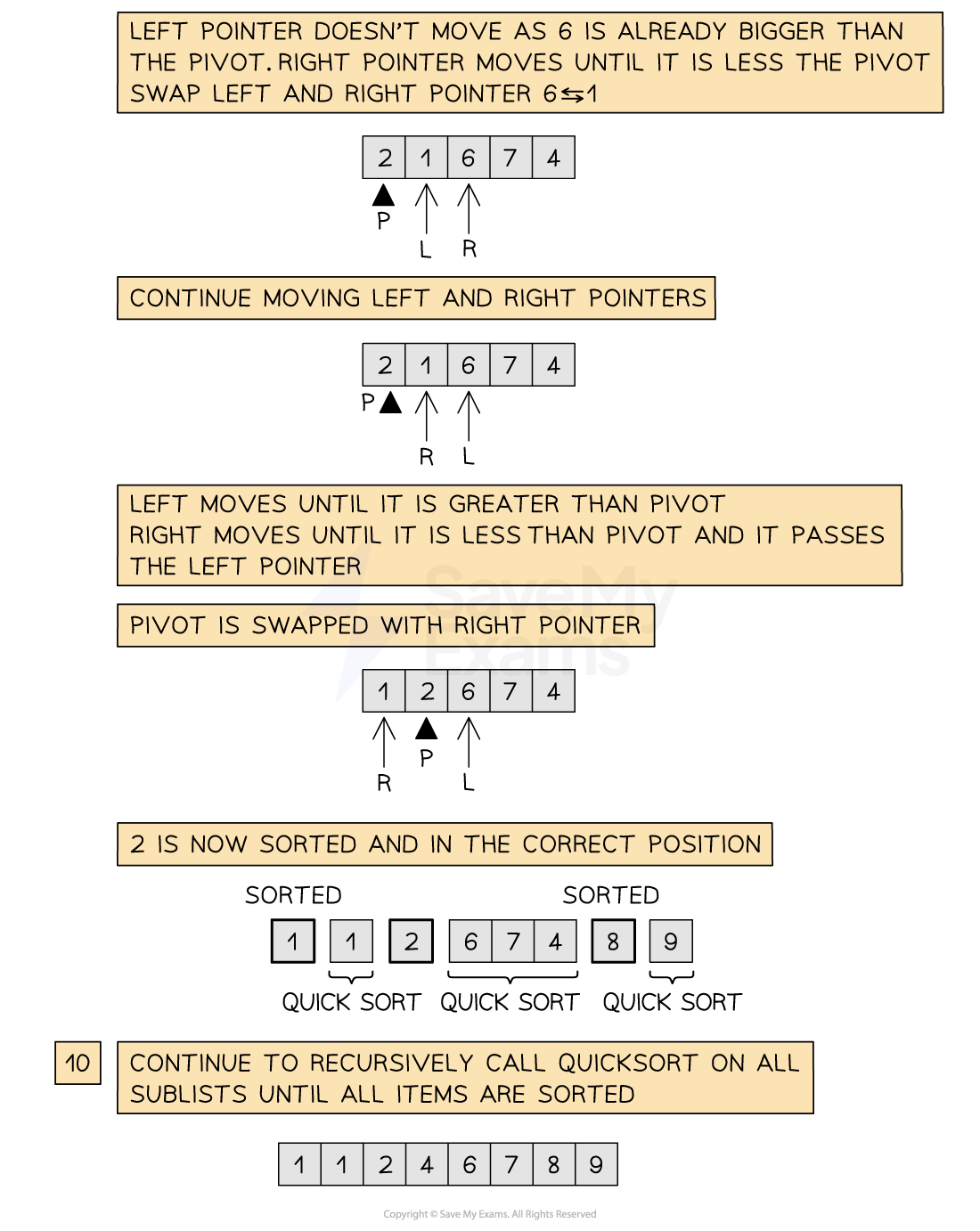
Figure 2: Performing the Quick sort

Time complexity of quick sort

• Quick sort is a divide and conquer algorithm that splits the problem into smaller subproblems using a pivot value

• The pivot divides the list into two parts: values less than the pivot and values greater than the pivot

• Each sub list is then sorted recursively until the list is completely ordered

Best and average case

• If the pivot divides the list roughly in the middle, the algorithm performs efficiently

• Each level of recursion performs n operations to partition the list

• There are approximately log n levels of recursion

• This gives a best and average case time complexity of O(n log n)

Worst case

• If the pivot is consistently placed at one extreme (for example, always the smallest or largest value), one partition becomes empty

• This causes the recursion to degenerate into a single chain of calls

• Each recursive call processes n – 1 elements, leading to n × (n – 1) operations, or O(n²) overall

• Poor pivot selection or already sorted input data can lead to this worst-case scenario

• In practice, randomised or median-of-three pivot selection is used to avoid the worst case

• If recursion depth becomes too large, a stack overflow can occur due to too many recursive calls

Space complexity of a quick sort

• Quick sort requires additional memory as copies of lists are made and put on the stack. The overall space complexity is therefore O(n) with O(n) additional space required

Tracing a quick sort

• The trace table below shows the process of calling the quick sort and moving the left and right pointers up and down the list to find elements to swap and then find the correct position of the pivot

• Once the pivot is in place, quick sort is recursively called on both sublists on either side of the pivot. Note that a second call to quick sort may not exist if the pivot value ends on either extreme of the list

• The process repeats, calling quick sort on progressively smaller sublists until all values are in the correct order

Trace Table for the Quick sort