dijkstras-shortest-path-algorithm

Dijkstra’s Shortest Path Algorithm

What is Dijkstra’s shortest path algorithm?

• In A Level Computer Science, Dijkstra’s shortest path algorithm is an example of an optimisation algorithm that calculates the shortest path from a starting location to all other locations

• Dijkstra’s uses a weighted graph in a similar manner to a breadth first search to exhaust all possible routes to find the optimal route to the destination node

• To revise Graphs you can follow this link

• Each route is represented as an arc/edge from a node/vertex. Each edge carries a weighted value which represents some measurement, for example time, distance or cost

• An illustrated example of Dijkstra’s is shown below

What is an optimisation problem?

• Optimisation problems involve maximising the efficiency of a solution to solve the stated problem. Examples of optimisation problems can include:

  • Finding the shortest route between two points. This is used for planning journeys, creating networks, building circuit boards, etc.

  • Minimising resource usage in manufacturing or games

  • Timetabling lessons in school or office meetings

  • Scheduling staff breaks and work hours

• The most common optimisation problem encountered in daily life is finding the shortest route from A to B. Various apps exist to calculate these distances, such as Google Maps or road trip planners

Performing Dijkstra’s shortest path algorithm

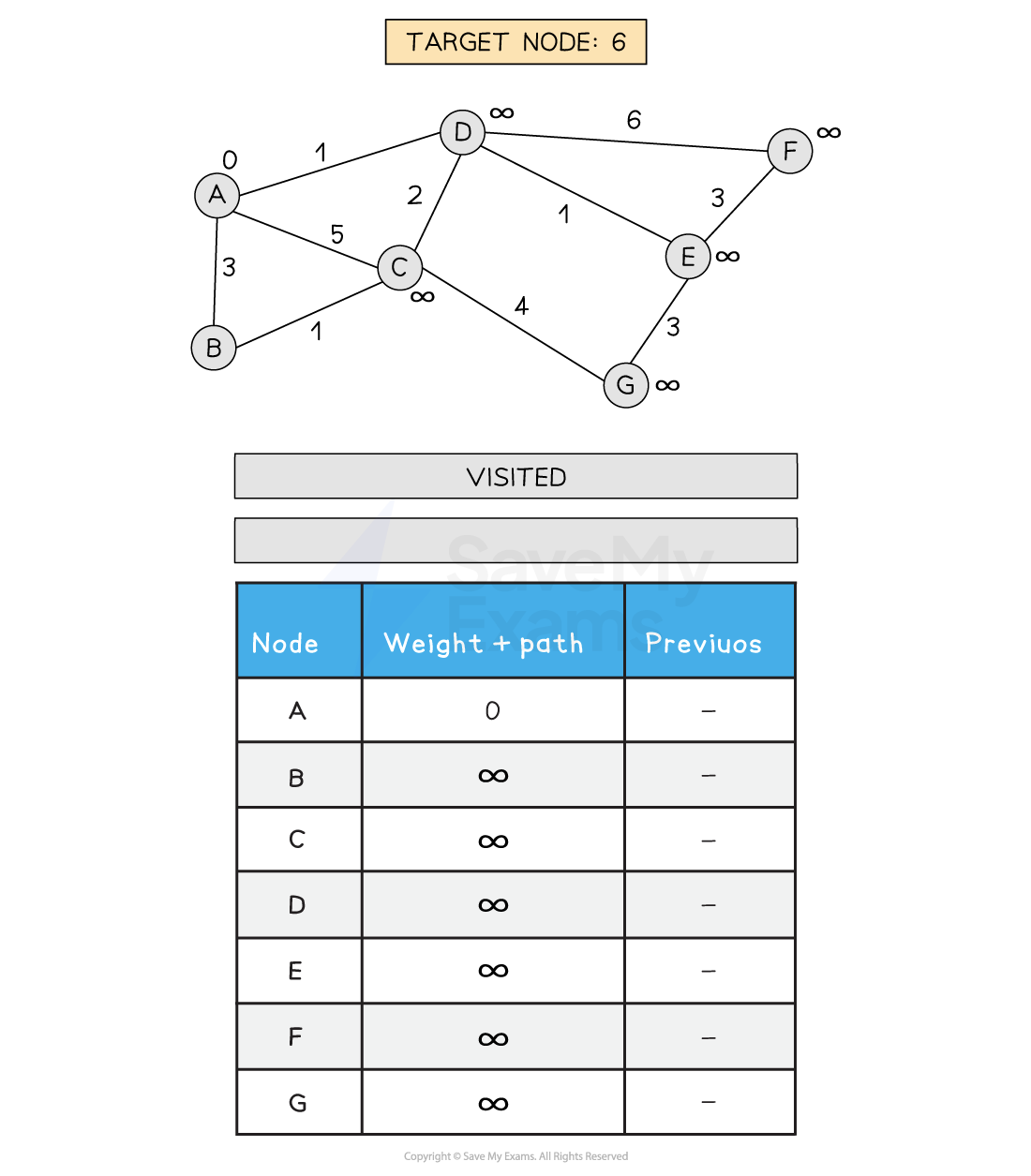
1) Set A path to 0 and all other path weights to infinity

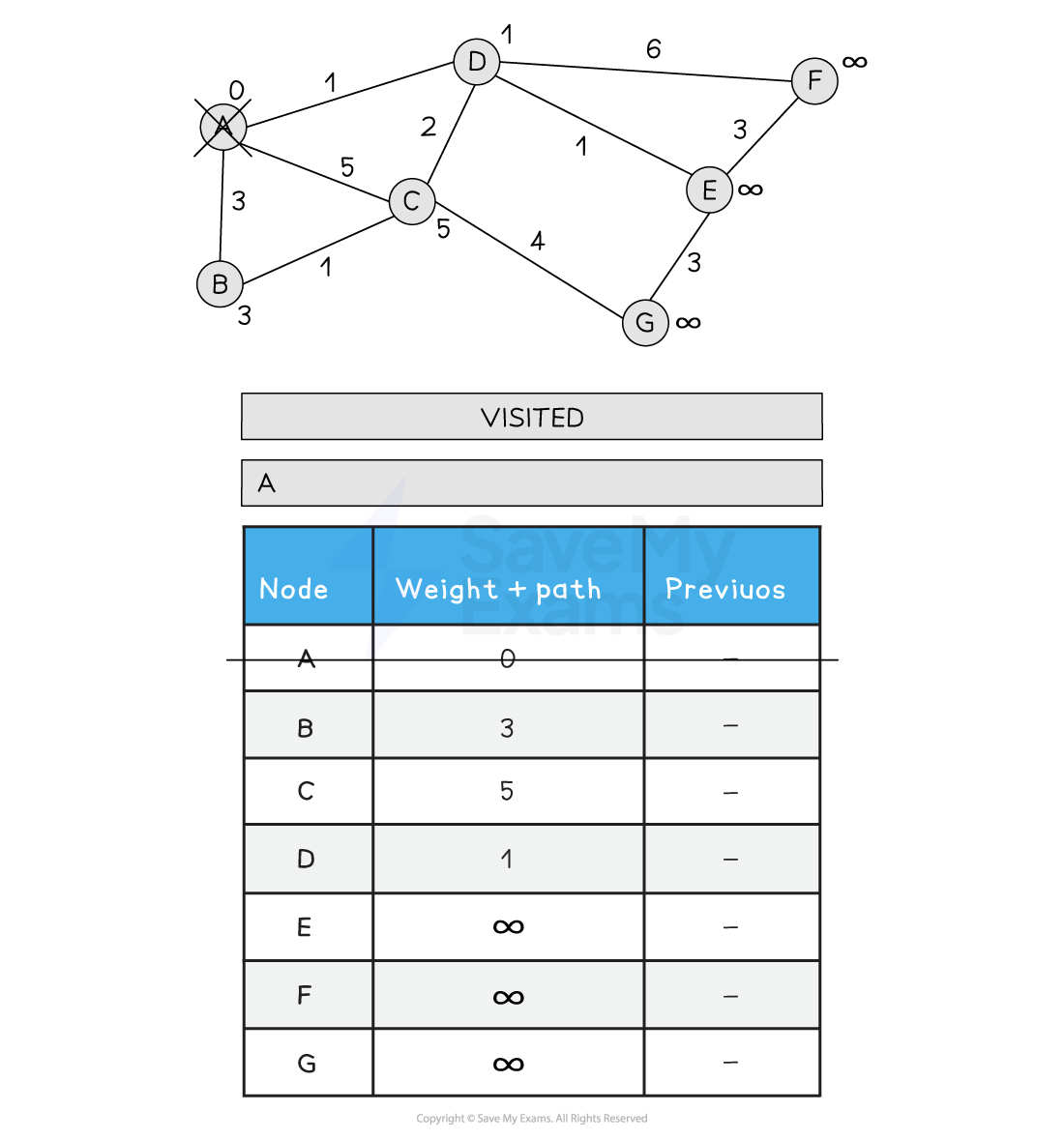
2) Visit A. Update all neighbouring nodes path weights to the distance from A + A’s path weight (0)

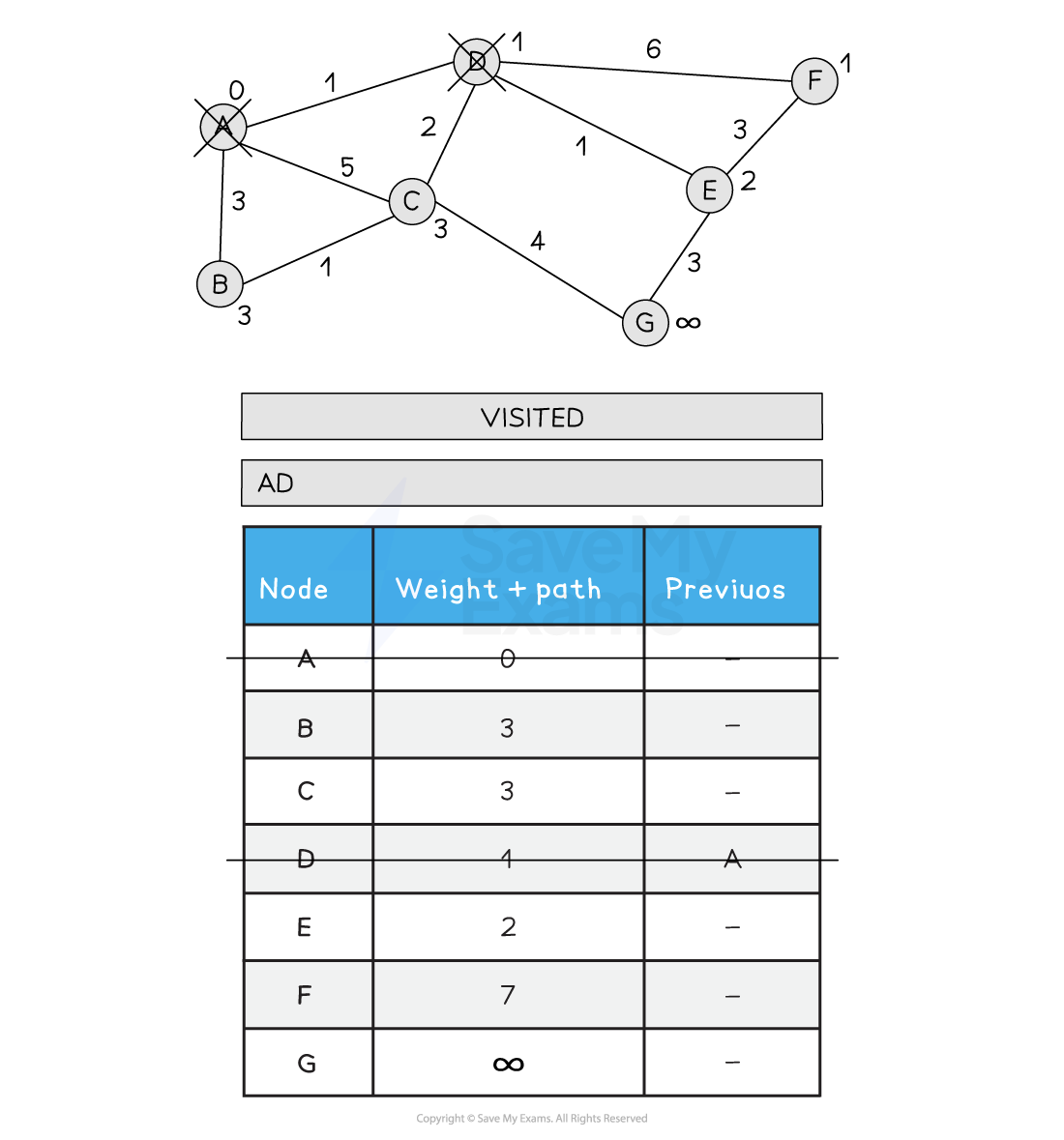
3) Choose the next node to visit that has the lowest path weight (D). Visit D. Update all neighbouring, non-visited nodes with a new path weight if the old path weight is bigger than the new path weight. C is updated from 5 to 3 as the new path is shorted (A > D > C)

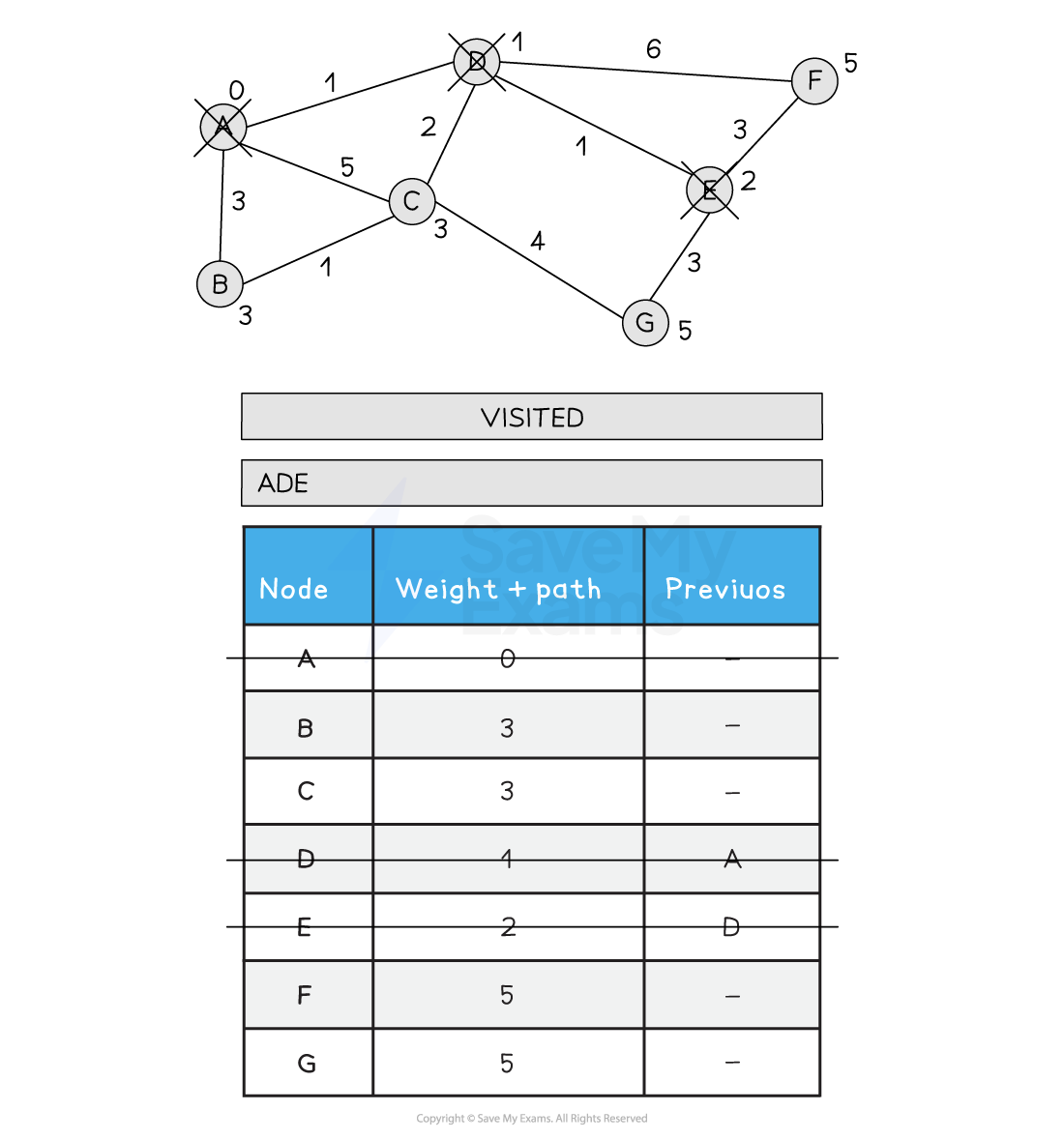
4) Choose the next node to visit that has the lowest path weight (E). Visit E. Update all neighbouring, non-visited nodes from E with a new path weight. F is updated from 7 to 5 as the new path is shorter (A > D > E > F)

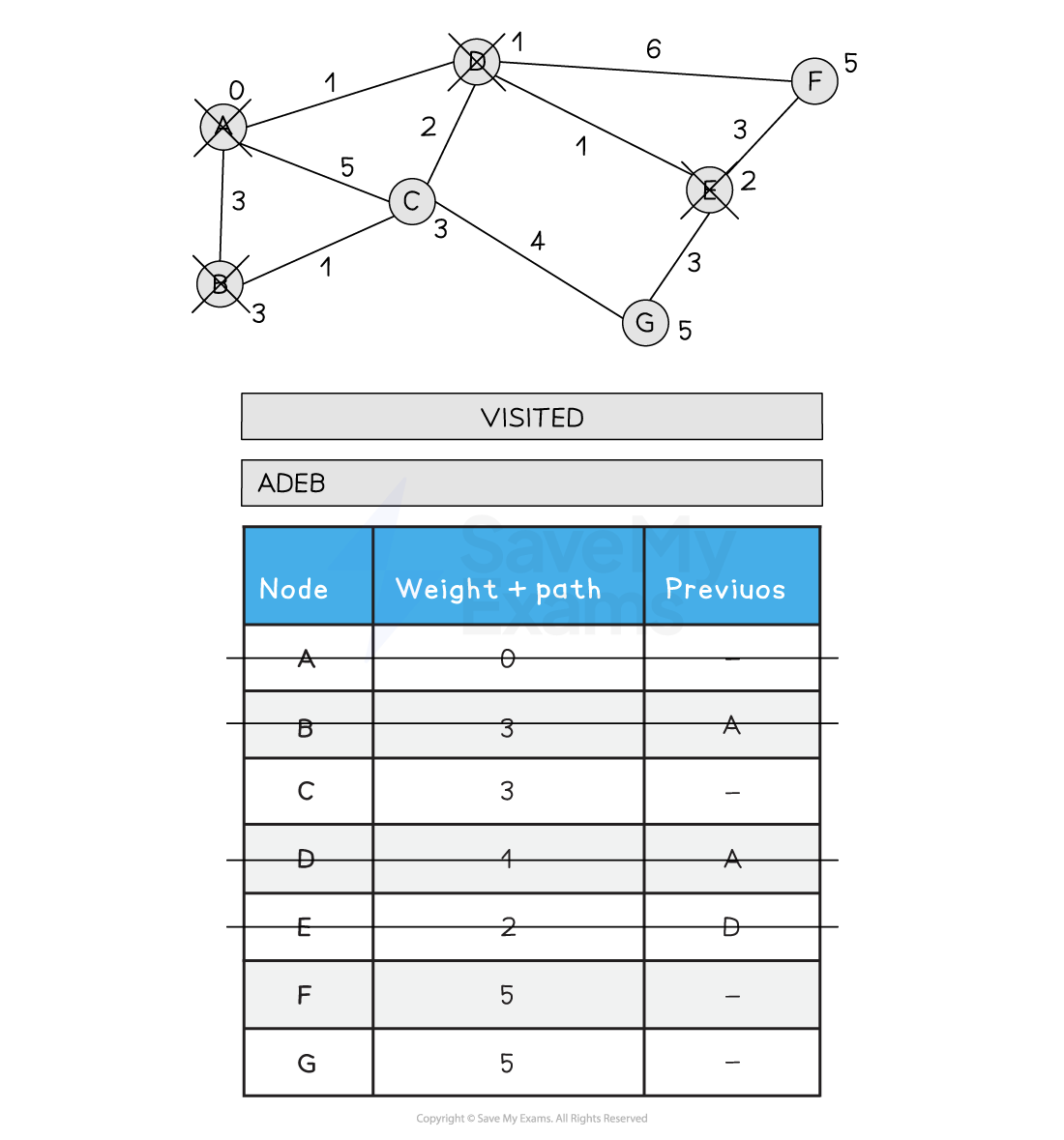
5) Choose the next node to visit, alphabetically (B). Visit B. Update all neighbouring non-visited nodes from B with a new weight if the path is less than the current path. C is not updated as A > B > C is 4

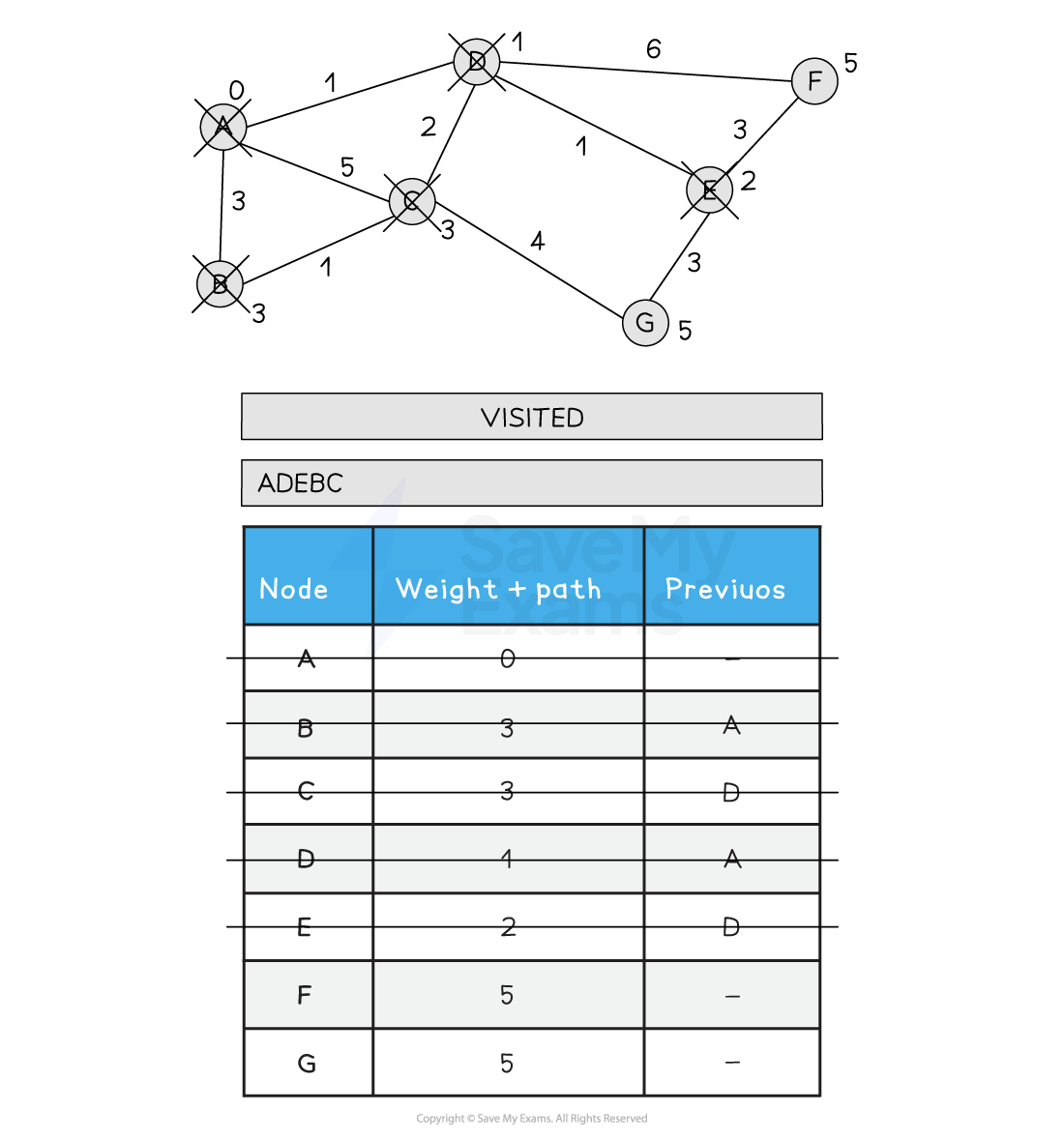
6) Choose the next lowest node and visit (C). Update C’s neighbours if the new path is shorter than the old path. A > D > C > G is 8, so G is not updated

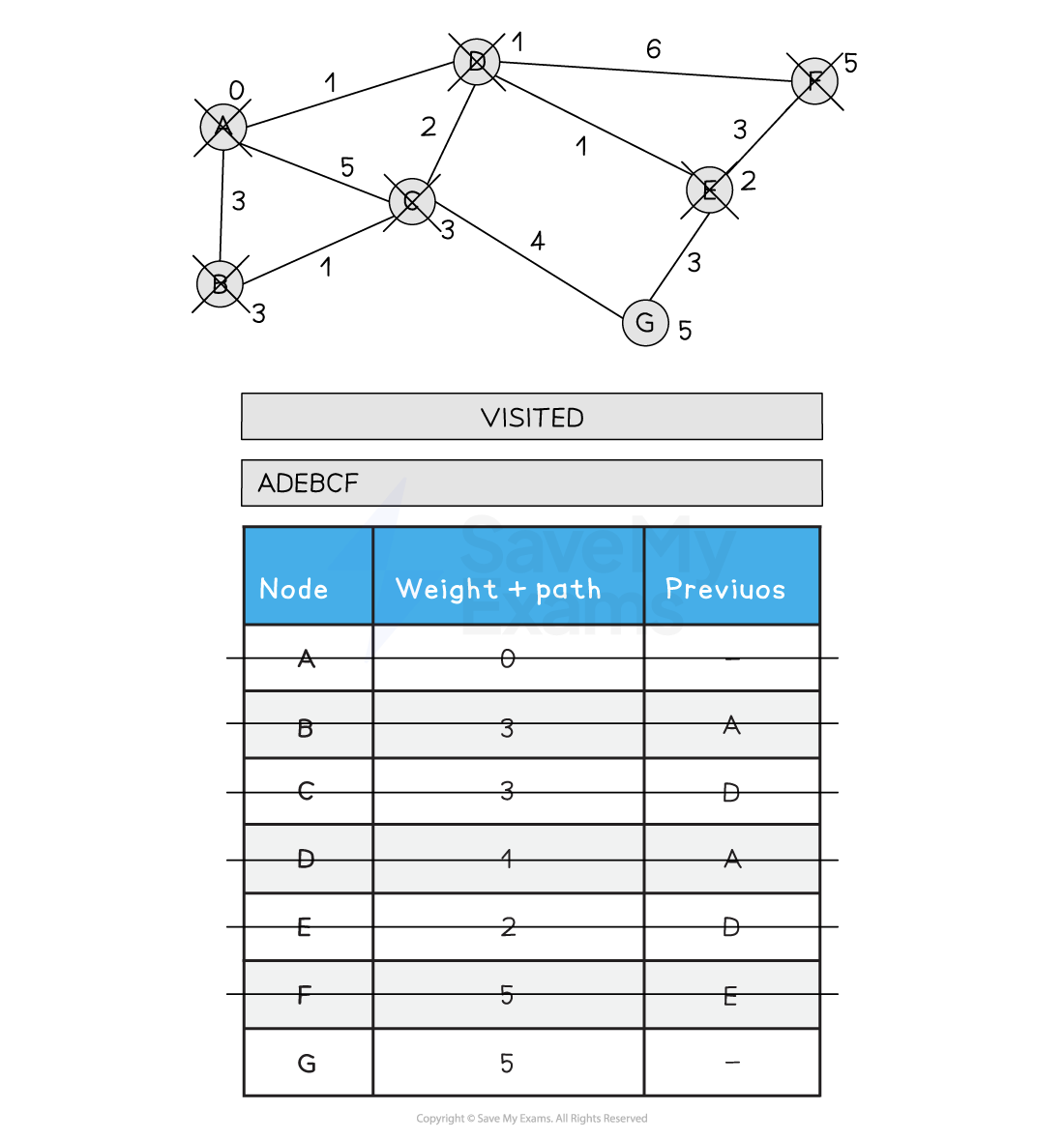
7) Choose the next lowest node and visit (F). Update F’s neighbours if the new path is shorter than the old path. F has no non-visited neighbours so no updates are made

<div class=”mb-5″