a-algorithm

A* algorithm

What is the A* algorithm?

• The A* (A-star) algorithm is a pathfinding algorithm that builds upon Dijkstra’s algorithm

• It introduces a heuristic function to improve efficiency

• It is used to find the shortest path from a starting node to a goal node in a graph

• While Dijkstra’s algorithm considers only the actual cost from the start node:

  • A* enhances this by estimating the remaining distance to the goal

  • This makes it more goal-oriented and often more efficient

How A* improves on Dijkstra’s

• To avoid inefficient detours, A* introduces a heuristic function, called h(x)

• It estimates the straight-line distance (Euclidean distance) from the current node to the goal

• A* combines both cost and estimate using the formula:

  • f(x) = g(x) + h(x)

    • g(x) = the actual cost from the start node to the current node

    • h(x) = the heuristic estimate to the goal node

    • f(x) = the total estimated cost of the cheapest solution through node x

• By choosing nodes with the lowest f(x) value, A* aims to explore paths that are both cheap and move closer to the goal

Heuristics in A*

• The heuristic function h(x) should never overestimate the true cost to the goal

• This ensures A* remains optimally efficient

• The closer h(x) is to the true cost, the fewer nodes A* needs to explore

• If h(x) increases, it may indicate the algorithm is moving away from the goal, helping it backtrack or choose a better path

• Below is an illustration of the A* search:

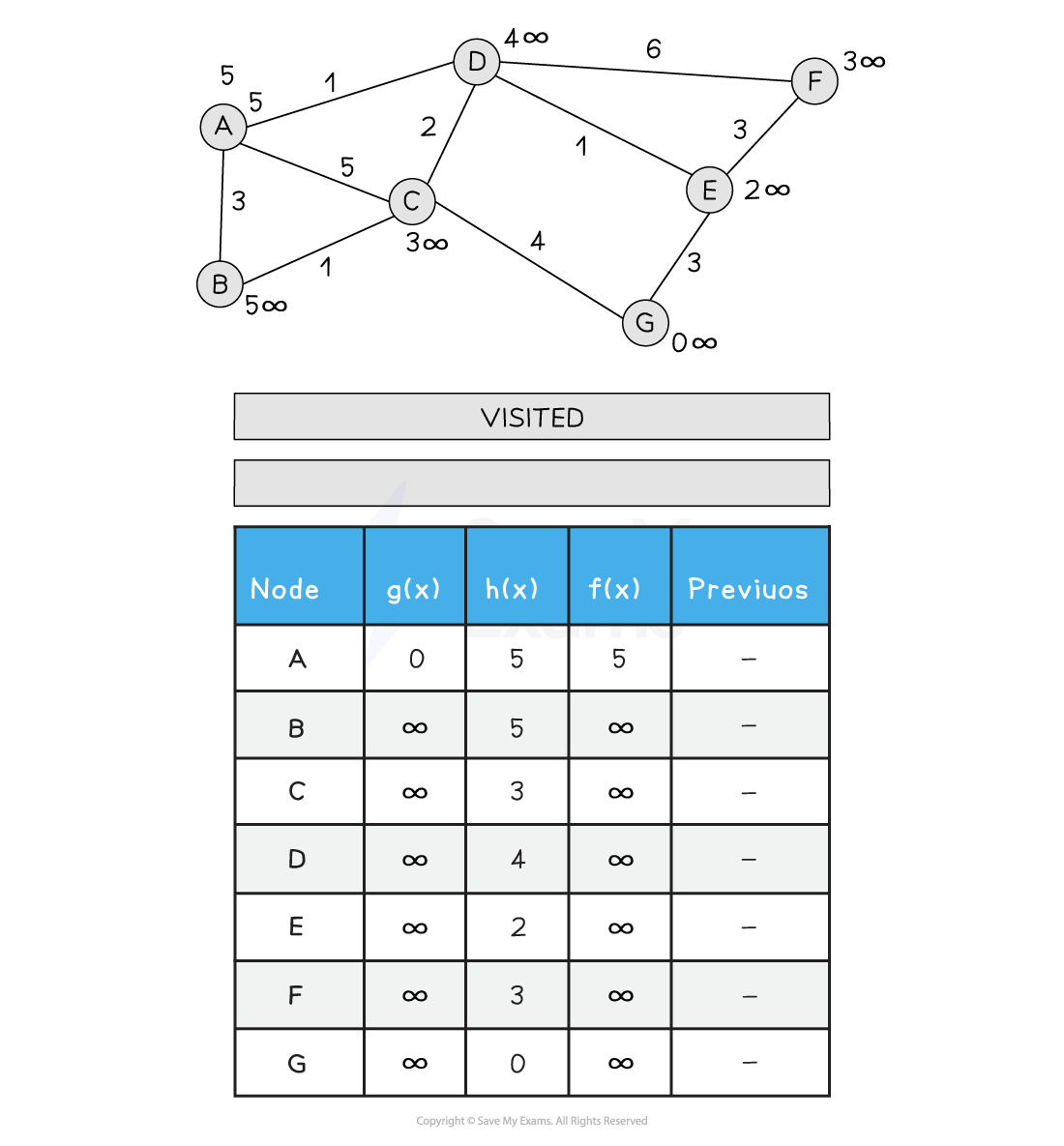
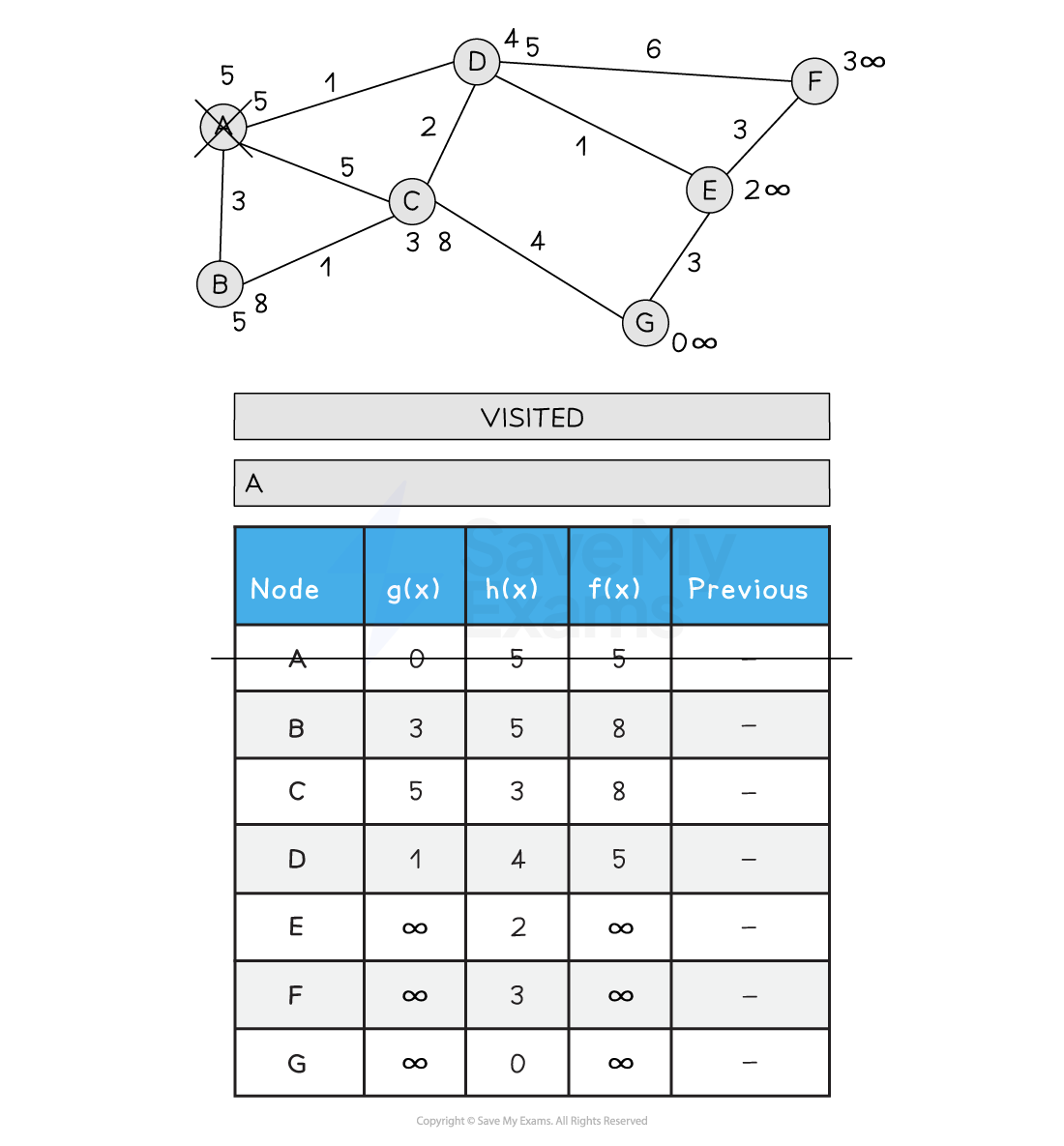
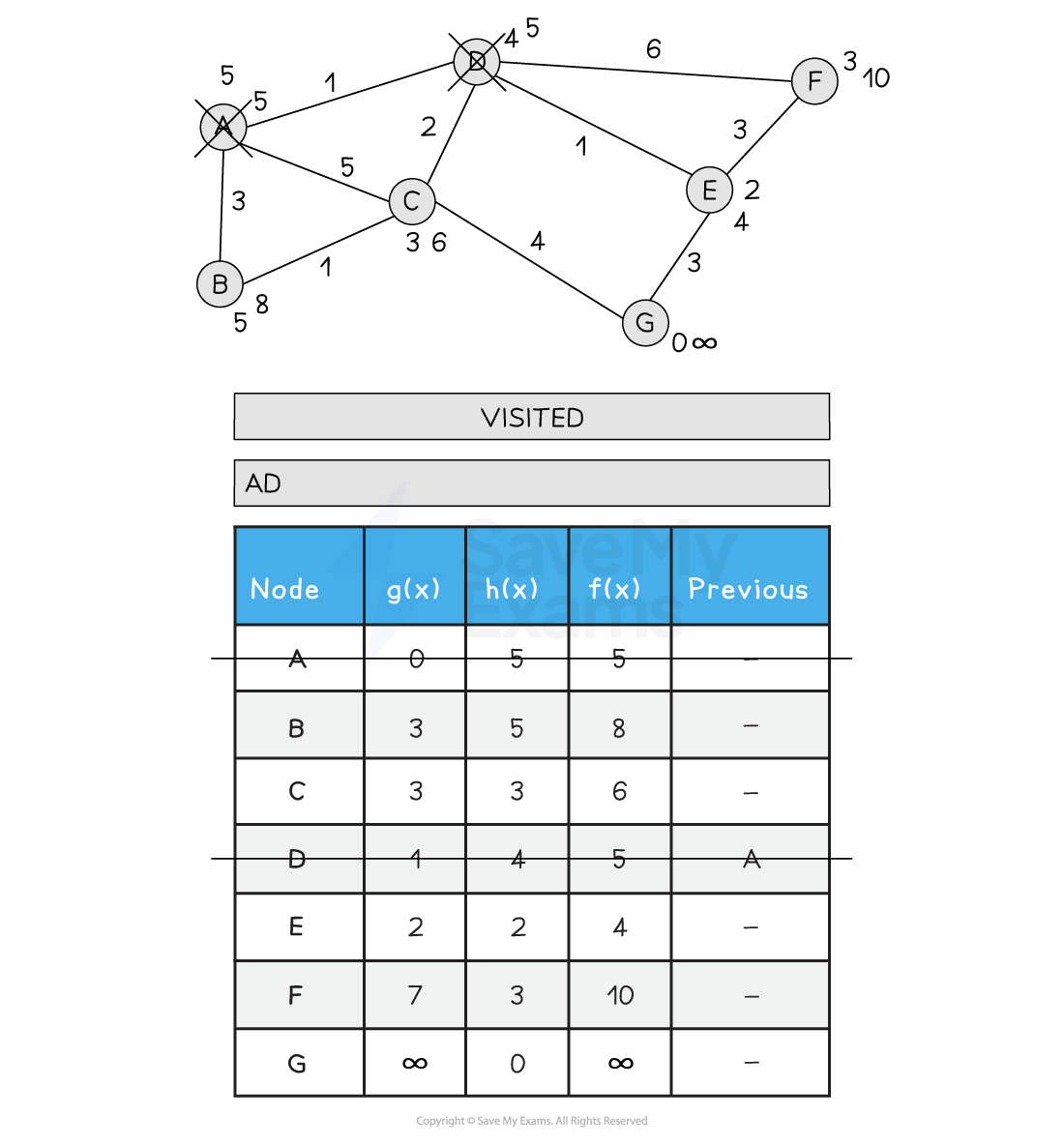
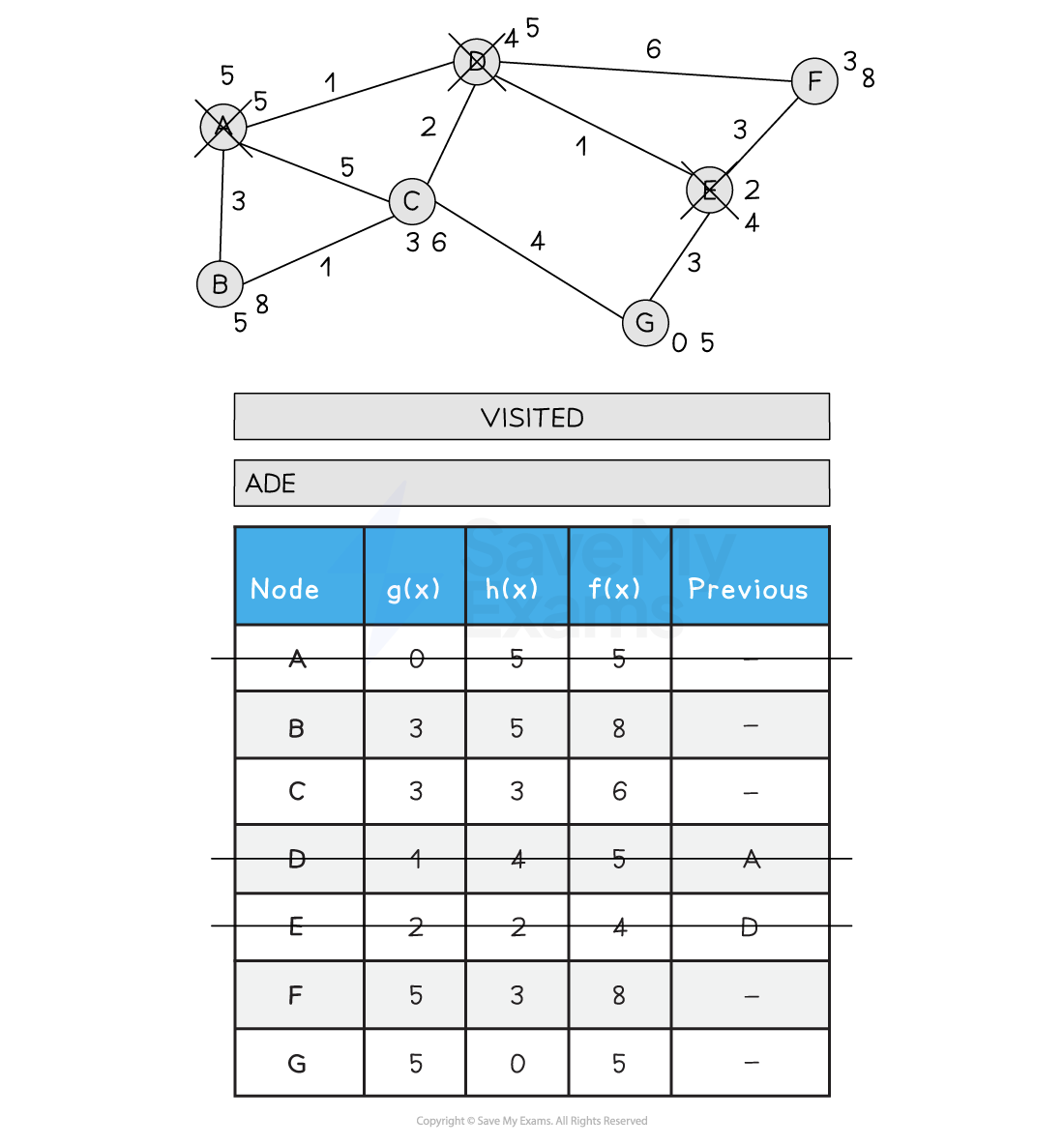
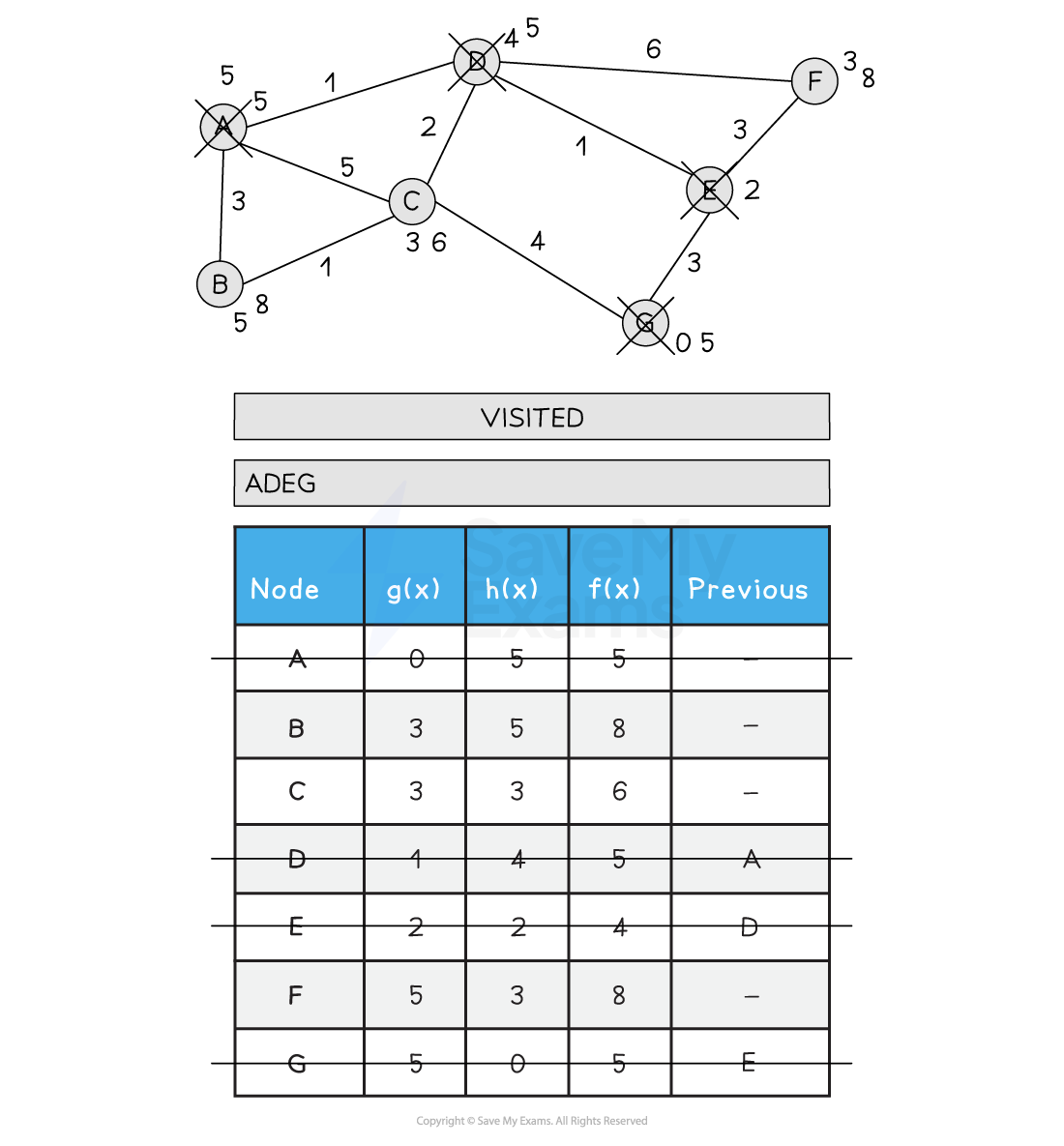
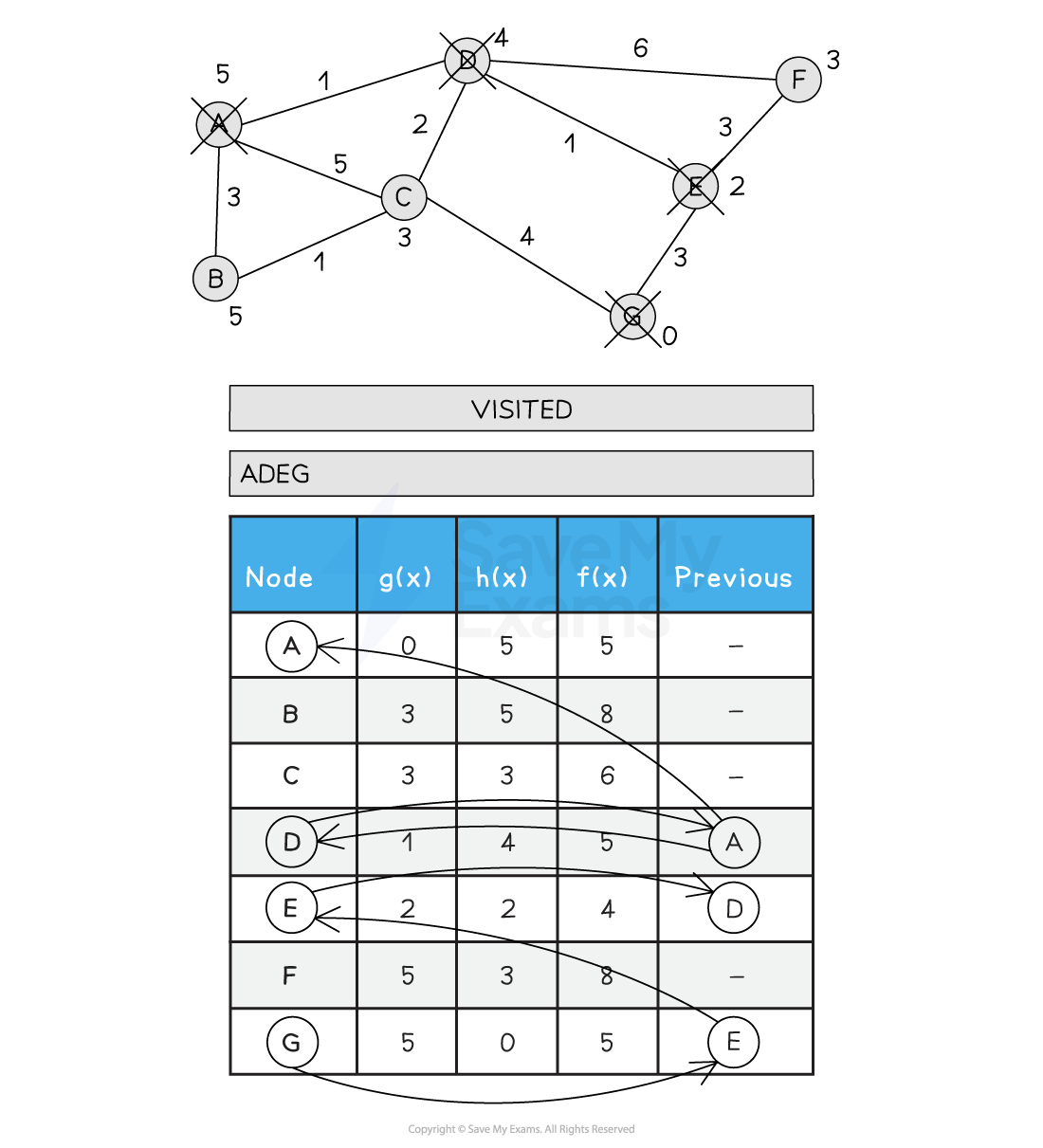
Figure 2: Performing the A* Search

A* vs Dijkstra’s

Programming A* algorithm

How do you write an A* algorithm?

Pseudocode

FUNCTION AStarSearch(graph, start, goal) // Initialise distances and f-scores FOR EACH node FROM graph SET g[node] TO infinity SET f[node] TO infinity NEXT node SET g[start] TO 0 SET f[start] TO h[start] DECLARE openSet AS LIST ADD start TO openSet WHILE openSet IS NOT EMPTY // Find node in openSet with the lowest f value SET min TO null FOR EACH node FROM openSet IF min = null THEN SET min TO node ELSEIF f[node] < f[min] THEN SET min TO node ENDIF NEXT node IF min = goal THEN EXIT WHILE ENDIF REMOVE min FROM openSet // Check all neighbours of current node FOR EACH neighbour FROM graph[min] SET tentativeG TO g[min] + cost(min, neighbour) IF tentativeG < g[neighbour] THEN SET g[neighbour] TO tentativeG SET f[neighbour] TO g[neighbour] + h[neighbour] SET previousNode[neighbour] TO min IF neighbour NOT IN openSet THEN ADD neighbour TO

• graph[min] assumes you’re storing adjacency lists

• h[node] is your heuristic table

• g[] and f[] are maps (dictionaries) for real cost and estimated total cost

• cost(min, neighbour) should be defined or assumed available

Python

def a_star_search(graph, start, goal, h): open_set = [start] g = {node: float('inf') for node in graph} f = {node: float('inf') for node in graph} came_from = {} g[start] = 0 f[start] = h[start] while open_set: # Get node with lowest f value current = min(open_set, key=lambda node: f[node]) if current == goal: break open_set.remove(current) for neighbour, cost in graph[current]: tentative_g = g[current] + cost if tentative_g < g[neighbour]: g[neighbour] = tentative_g f[neighbour] = g[neighbour] + h[neighbour] came_from[neighbour] = current if neighbour not in open_set: open_set.append(neighbour) # Reconstruct path path = [] node = goal while node != start: path.append(node) node = came_from[node] path.append(start) path.reverse() return path

Example usage:

graph = { 'A': [('B', 2), ('C', 5)], 'B': [('D', 4)], 'C': [('D', 1)], 'D': [('E', 3)], 'E': []
} h = { 'A': 7, 'B': 6, 'C': 4, 'D': 2, 'E': 0
} print(a_star_search(graph, 'A', 'E', h))

Output:

• A possible shortest path from 'A' to 'E', guided by the heuristic values